مسابقهٔ ریاضی - صفحه 3 از 4

مسئلهٔ ۲ – مسابقهٔ ریاضی تکمیلی – مهر ۹۸

یک‌بار توزین یاتاقان یک کارگاه بزرگ تولید قطعات یدکی ماشین، برای استخدام مهندسی با هوش استثنایی در روزنامه آگهی داد. بعد از چند بار غربال متقاضیان، دو نفر باقی ماندند. سرمهندس به آنها گفت: در اینجا $200$ جعبه وجود دارد. در هر جعبه $500$ یاتاقان، هریک به وزن یک پوند، قرار دارد. اشتباهی، نوعی قدیمی […]

مسئلهٔ ۱ – مسابقهٔ ریاضی تکمیلی – مهر ۹۸

جرج و ویلیام همراه همسرانشان، کاترین و الیزابت، چند بسته شکلات خریده‌اند. پس از خرید، جرج یادآور شد که مقدار پولی که به دلار برای هر بسته داده برابر با تعداد بسته‌های شکلاتی است که خریده است. وقتی فهمیدند این وضعیت در مورد سه نفر دیگر، یعنی ویلیام، کاترین و الیزابت، هم پیش آمده بسیار […]

مسئلهٔ ۴ – مسابقهٔ ریاضی تکمیلی – شهریور ۹۸

فرض کنید $n$ یک عدد طبیعی زوج باشد. اگر برای هریک از اعداد اول بزرگ‌تر یا مساوی $\frac{n}{2}$، مانند $p$، عدد اولی مانند $q$ وجود داشته باشد به‌طوری‌که $p+q=n$، آن‌وقت $n$ را یک عدد زوج فراگُلدباخی می‌نامیم. مثال ۱. عدد $10$ یک عدد زوج فراگُلدباخی است. زیرا اعداد اول بزرگ‌تر یا مساوی $\frac{10}{2}$ عبارتند از: […]

مسئلهٔ ۳ – مسابقهٔ ریاضی تکمیلی – شهریور ۹۸

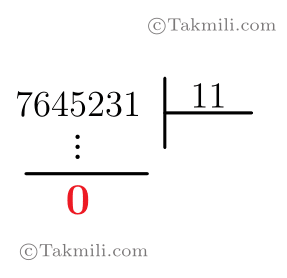
«حاصل‌جمع منفی‌مثبتِ» عدد $23485$ برابر است با: \[2-3+4-8+5=0.\]در حالت کلی، برای به‌دست آوردن حاصل‌جمع منفی‌مثبتِ یک عدد طبیعی، بین رقم‌های آن عدد، از چپ به راست و یکی‌درمیان، علامت‌های $-$ و $+$ قرار می‌دهیم و حاصل عبارت را محاسبه می‌کنیم. یک عدد طبیعی بر $11$ بخش‌پذیر است هروقت حاصل‌جمع منفی‌مثبتِ آن عدد بر $11$ بخش‌پذیر […]

مسئلهٔ ۲ – مسابقهٔ ریاضی تکمیلی – شهریور ۹۸

در شکل زیر، نقطه‌های $E$ و $F$ به‌ترتیب روی پاره‌خط‌های $AB$ و $AD$ قرار دارند. نقطهٔ $G$ محل برخورد پاره‌خط‌های $AC$ و $BD$ است. همچنین، پاره‌خط‌های $AG$، $BF$، و $DE$ یکدیگر را در نقطهٔ $H$ قطع کرده‌اند. اگر $x$ یک عدد باشد و $\bullet$ مساحت مثلث $AFH$ برابر $4x+4$، $\bullet$ مساحت مثلث $DFH$ برابر $2x+20$، […]

مسئلهٔ ۱ – مسابقهٔ ریاضی تکمیلی – شهریور ۹۸

به دنباله‌هایی عددی مانند دنبالهٔ\[11,13,15,17,19\]که جمله‌ٔ دوم به بعد آن، از جمع زدن جملهٔ قبلی با مقدار ثابتی به‌دست می‌آید، دنبالهٔ حسابی می‌گویند. در دنبالهٔ بالا، جملهٔ اول عدد $11$ است و هریک از جمله‌های بعدی از جمع کردن عدد $2$ با جملهٔ قبلی به‌دست می‌آیند. مثال دیگری از دنبالهٔ حسابی:\[10,5,0,-5,-10,-15,\dots.\] می‌خواهیم خانه‌های خالی جدول […]

مسئلهٔ ۴ – مسابقهٔ ریاضی تکمیلی – مرداد ۹۸

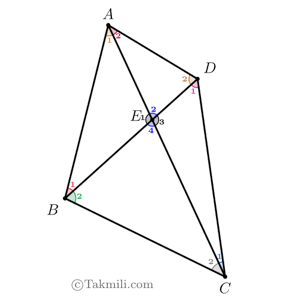
در چهارضلعی $ABCD$، دو قطر $AC$ و $BD$ یکدیگر را در نقطهٔ $E$ قطع کرده‌اند. می‌دانیم سه پاره‌خط $AB$، $BC$، و $BD$ برابرند و اندازهٔ زاویهٔ $CBD$ دو برابر اندازهٔ زاویهٔ $DBA$ است. دوازده زاویهٔ داخلی مثلث‌های $AEB$، $BEC$، $CED$، و $DEA$ را در نظر بگیرید. اگر اندازهٔ همهٔ این دوازده‌تا زاویه، برحسب درجه، اعدادی […]

مسئلهٔ ۳ – مسابقهٔ ریاضی تکمیلی – مرداد ۹۸

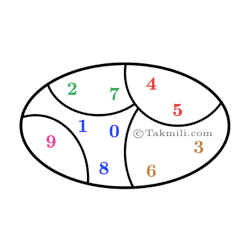
اعداد زیر را در نظر بگیرید: \[0,1,2,3,4,5,6,7,8,9.\]به روش‌های مختلفی می‌توان اعداد بالا را به دو یا چند گروه تقسیم کرد. برای مثال، می‌توان این اعداد را به چهار گروه تقسیم کرد: \[\begin{aligned}&\bullet\;0,3,4,5\\&\bullet\;2,9\\&\bullet\;7\\&\bullet\;1,6,8.\end{aligned}\] مجموع اعداد هریک از گروه‌های بالا برابر است با: \[\begin{aligned}&\bullet\;0+3+4+5=12\\&\bullet\;2+9=11\\&\bullet\;7=7\\&\bullet\;1+6+8=15.\end{aligned}\] به چند روش می‌توان اعداد $0$، $1$، $2$، $3$، $4$، $5$، $6$، $7$، […]

مسئلهٔ ۲ – مسابقهٔ ریاضی تکمیلی – مرداد ۹۸

یک مکعب‌مستطیل توپُر $8\times8\times n$، از مکعب‌های $1\times1\times1$ ساخته شده است. فرض کنید $A$ مساحت کل مکعب‌مستطیل، و $B$ مجموع مساحت کل مکعب‌های $1\times1\times1$ سازندهٔ مکعب‌مستطیل باشد. همهٔ $n$هایی را پیدا کنید که برای آنها، $\frac{B}{A}$ عددی طبیعی باشد. راهنمایی: شکل زیر، مثالی است که در آن $n=5$. در این مثال، $\frac{B}{A}$ عددی طبیعی نیست! […]

مسئلهٔ ۱ – مسابقهٔ ریاضی تکمیلی – مرداد ۹۸

می‌خواهیم خانه‌های خالی زیر را با اعداد $1$، $2$، $3$، $4$، $5$، $6$، $7$، و $8$ پر کنیم به‌طوری‌که مجموع اعداد روی هر ضلع با مجموع اعداد روی هریک از دو ضلع دیگر برابر باشد. (تکرار اعداد مجاز نیست.)اگر مجموع اعداد روی هر ضلع را با $S$ نمایش دهیم، آن‌وقت همهٔ مقدارهای ممکن $S$ را […]

دسته: مسابقهٔ ریاضی