نهم. فصل ۳. قضیهٔ زاویههای متقابل بهرأس

قضیهٔ زاویههای متقابلبهرأس. زاویههای متقابلبهرأس برابرند. فرض: دو زاویه متقابل بهرأس هستند. حکم: این دو زاویه برابرند. اثبات. در شکل زیر، دو خط \(AC\) و \(BD\) یکدیگر را در نقطهٔ \(O\) قطع کردهاند. میخواهیم ثابت کنیم که زاویههای متقابلبهرأس \(AOB\) و \(COD\) برابرند. برای سادگی، زاویههای \(AOB\)، \(AOD\)، و \(COD\) را بهترتیب با \(O_1\)، \(O_2\)، […]
نهم. فصل ۳. قضیهٔ خطوط موازی و مورب و عکس آن

قضیه خطوط موازی و مورب. اگر خط $d$ دو خط موازی$\ell_1$ و $\ell_2$ را قطع کند و زاویههای $A_1$ و $B_1$ را پدید آورد، آنگاه $\widehat{A}_1=\widehat{B}_1$. فرض. مطابق شکل بالا، خط $d$ دو خط موازی$\ell_1$ و $\ell_2$ را قطع کرده و زاویههای $A_1$ و $B_1$ را پدید آورده است. حکم. $\widehat{A}_1=\widehat{B}_1$. اثبات. از برهان خلف […]
نهم. فصل ۳. قضیهٔ مجموع زاویههای مثلث

قضیهٔ مجموع زاویههای مثلث. مجموع زاویههای هر مثلث \(180\) درجه است. فرض. یک مثلث دلخواه داریم. حکم. مجموع زوایای این مثلث \(180\) درجه است. اثبات. مثلث \(ABC\) را در نظر بگیرید. میخواهیم ثابت کنیم \(\widehat{A}+\widehat{B}+\widehat{C}=180^\circ\). از \(A\) خطی موازی با \(BC\) رسم میکنیم و برای سادگی، زاویههای را بهصورت زیر نامگذاری میکنیم. چون \(\ell\) و \(BC\) […]
نهم. فصل ۳. قضیهٔ زاویهٔ خارجی مثلث

قضیهٔ زاویه خارجی مثلث. اندازهٔ هر زاویهٔ خارجی در یک مثلث دلخواه برابر است با مجموع اندازههای زاویههای داخلی غیرمجاورش. فرض. یک مثلث دلخواه داریم. حکم. اندازهٔ هر زاویهٔ خارجی در این مثلث برابر است با مجموع اندازههای زاویههای داخلی غیرمجاورش. اثبات. مطابق شکل زیر، فرض کنیم زاویهٔ \(ACD\) زاویهٔ خارجی مثلث \(ABC\) باشد. میخواهیم […]
نهم. فصل ۳. اصل ضزض

اصل ضزض (دو ضلع و زاویه بین). اگر دو ضلع و زاویهٔ بین آنها از مثلثی با دو ضلع و زاویهٔ بین آنها از مثلثی دیگر برابر باشند، آنگاه این دو مثلث همنهشتاند. فرض. دو ضلع و زاویهٔ بین آنها از مثلثی با دو ضلع و زاویهٔ بین آنها از مثلثی دیگر برابر هستند. حکم. […]
نهم. فصل ۳. قضیهٔ زضز
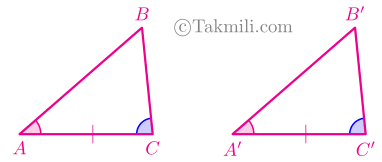
قضیهٔ زضز. اگر دو زاویه و ضلع بین آنها از مثلثی با اجزاء نظیر آنها از مثلثی دیگر برابر باشند، آنگاه این دو مثلث همنهشتاند. فرض. دو زاویه و ضلع بین آنها از مثلثی با اجزاء نظیر آنها از مثلثی دیگر برابر هستند. حکم. این دو مثلث همنهشتاند. اثبات. فرض کنیم دو مثلث \(ABC\) و […]
نهم. فصل ۳. قضیهٔ ضضض

قضیهٔ ضضض. اگر سه ضلع از مثلثی با سه ضلع از مثلثی دیگر برابر باشد، آنگاه این دو مثلث همنهشتاند. فرض. سه ضلع از مثلثی با سه ضلع از مثلثی دیگر برابر هستند. حکم. این دو مثلث همنهشت هستند. اثبات. فرض کنیم که در دو مثلث \(ABC\) و \(DEF\) داشته باشیم \(AB=DE\)، \(AC=DF\)، و \(BC=EF\). […]
نهم. فصل ۳. قضیهٔ ززض

قضیهٔ ززض. اگر دو زاویه و ضلع غیر بین آنها از یک مثلث با دو زاویه و ضلع غیر بین آنها از مثلثی دیگر، نظیر به نظیر برابر باشند، آنگاه این دو مثلث همنهشتاند. فرض. دو زاویه و ضلع غیربین آنها از یک مثلث با اجزاء نظیر از مثلثی دیگر برابر است. حکم. این دو […]
نهم. فصل ۳. قضیهٔ عمودمنصف و عکس آن

قضیهٔ عمودمنصّف. هر نقطه روی عمودمنصّفِ یک پارهخط از دو سر آن پارهخط فاصلهٔ یکسان دارد. عکس قضیهٔ عمودمنصّف. اگر نقطهای از دو سر یک پارهخط فاصلهٔ یکسان داشته باشد، این نقطه روی عمودمنصّف پارهخط قرار دارد. فرض. نقطهای مانند \(M\) روی عمودمنصف پارهخطی، مانند \(AB\)، قرار دارد. حکم. \(MA=MB\). اثبات قضیهٔ عمود منصف. فرض […]
نهم. فصل ۳. قضیه مثلث متساویالساقین و عکس آن
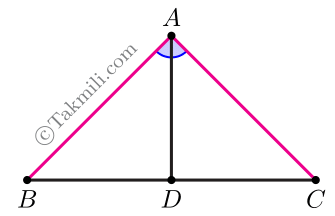
قضیهٔ مثلث متساوی الساقین. در هر مثلث متساویالساقین زاویههای پای ساق باهم برابرند. عکس قضیهٔ مثلث متساوی الساقین. اگر مثلثی دو زاویهٔ برابر داشته باشد، آن مثلث متساویالساقین است. فرض. یک مثلث، مانند \(ABC\) به رأس \(A\)، متساویالساقین است. حکم. زاویههای \(ABC\) و \(ACB\) برابرند. در عکس قضیه، جای فرض و حکم عوض میشود. اثبات […]