اعداد فراگلدباخی

فرض کنید \(n\) یک عدد طبیعی زوج باشد. اگر برای هریک از اعداد اول بزرگتر یا مساوی \(\frac{n}{2}\)، مانند \(p\)، عدد اولی مانند \(q\) وجود داشته باشد بهطوریکه \(p+q=n\)، آنوقت \(n\) را یک عدد زوج فراگُلدباخی مینامیم. مثال ۱. عدد \(10\) یک عدد زوج فراگُلدباخی است. زیرا اعداد اول بزرگتر یا مساوی \(\frac{10}{2}\) عبارتند از: […]
پاسخ تشریحی مسئلهٔ ۳ – مسابقهٔ ریاضی تکمیلی – شهریور ۹۸
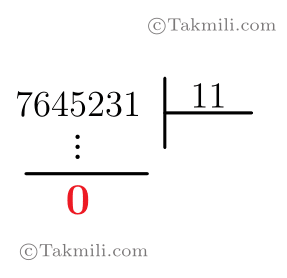
«حاصلجمع منفیمثبتِ» عدد \(23485\) برابر است با: \[2-3+4-8+5=0.\]در حالت کلی، برای بهدست آوردن حاصلجمع منفیمثبتِ یک عدد طبیعی، بین رقمهای آن عدد، از چپ به راست و یکیدرمیان، علامتهای \(-\) و \(+\) قرار میدهیم و حاصل عبارت را محاسبه میکنیم. یک عدد طبیعی بر \(11\) بخشپذیر است هروقت حاصلجمع منفیمثبتِ آن عدد بر \(11\) بخشپذیر […]
مسئلهٔ ۴ – مسابقهٔ ریاضی تکمیلی – شهریور ۹۸

فرض کنید \(n\) یک عدد طبیعی زوج باشد. اگر برای هریک از اعداد اول بزرگتر یا مساوی \(\frac{n}{2}\)، مانند \(p\)، عدد اولی مانند \(q\) وجود داشته باشد بهطوریکه \(p+q=n\)، آنوقت \(n\) را یک عدد زوج فراگُلدباخی مینامیم. مثال ۱. عدد \(10\) یک عدد زوج فراگُلدباخی است. زیرا اعداد اول بزرگتر یا مساوی \(\frac{10}{2}\) عبارتند از: […]
پاسخ تشریحی مسئلهٔ ۲ – مسابقهٔ ریاضی تکمیلی – شهریور ۹۸

در شکل زیر، نقطههای \(E\) و \(F\) بهترتیب روی پارهخطهای \(AB\) و \(AD\) قرار دارند. نقطهٔ \(G\) محل برخورد پارهخطهای \(AC\) و \(BD\) است. همچنین، پارهخطهای \(AG\)، \(BF\)، و \(DE\) یکدیگر را در نقطهٔ \(H\) قطع کردهاند. اگر \(x\) یک عدد باشد و \(\bullet\) مساحت مثلث \(AFH\) برابر \(4x+4\)، \(\bullet\) مساحت مثلث \(DFH\) برابر \(2x+20\)، […]
مسئلهٔ ۳ – مسابقهٔ ریاضی تکمیلی – شهریور ۹۸

«حاصلجمع منفیمثبتِ» عدد \(23485\) برابر است با: \[2-3+4-8+5=0.\]در حالت کلی، برای بهدست آوردن حاصلجمع منفیمثبتِ یک عدد طبیعی، بین رقمهای آن عدد، از چپ به راست و یکیدرمیان، علامتهای \(-\) و \(+\) قرار میدهیم و حاصل عبارت را محاسبه میکنیم. یک عدد طبیعی بر \(11\) بخشپذیر است هروقت حاصلجمع منفیمثبتِ آن عدد بر \(11\) بخشپذیر […]
پاسخ تشریحی مسئلهٔ ۱ – مسابقهٔ ریاضی تکمیلی – شهریور ۹۸
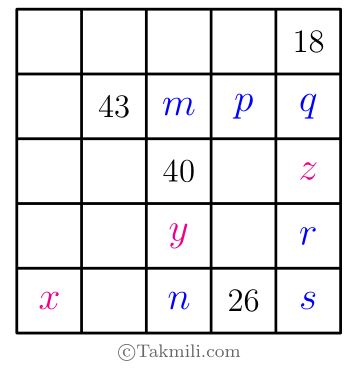
به دنبالههایی عددی مانند دنبالهٔ\[11,13,15,17,19\]که جملهٔ دوم به بعد آن، از جمع زدن جملهٔ قبلی با مقدار ثابتی بهدست میآید، دنبالهٔ حسابی میگویند. در دنبالهٔ بالا، جملهٔ اول عدد \(11\) است و هریک از جملههای بعدی از جمع کردن عدد \(2\) با جملهٔ قبلی بهدست میآیند. مثال دیگری از دنبالهٔ حسابی:\[10,5,0,-5,-10,-15,\dots.\] میخواهیم خانههای خالی جدول […]
مسئلهٔ ۲ – مسابقهٔ ریاضی تکمیلی – شهریور ۹۸

در شکل زیر، نقطههای \(E\) و \(F\) بهترتیب روی پارهخطهای \(AB\) و \(AD\) قرار دارند. نقطهٔ \(G\) محل برخورد پارهخطهای \(AC\) و \(BD\) است. همچنین، پارهخطهای \(AG\)، \(BF\)، و \(DE\) یکدیگر را در نقطهٔ \(H\) قطع کردهاند. اگر \(x\) یک عدد باشد و \(\bullet\) مساحت مثلث \(AFH\) برابر \(4x+4\)، \(\bullet\) مساحت مثلث \(DFH\) برابر \(2x+20\)، […]
مسئلهٔ ۱ – مسابقهٔ ریاضی تکمیلی – شهریور ۹۸

به دنبالههایی عددی مانند دنبالهٔ\[11,13,15,17,19\]که جملهٔ دوم به بعد آن، از جمع زدن جملهٔ قبلی با مقدار ثابتی بهدست میآید، دنبالهٔ حسابی میگویند. در دنبالهٔ بالا، جملهٔ اول عدد \(11\) است و هریک از جملههای بعدی از جمع کردن عدد \(2\) با جملهٔ قبلی بهدست میآیند. مثال دیگری از دنبالهٔ حسابی:\[10,5,0,-5,-10,-15,\dots.\] میخواهیم خانههای خالی جدول […]