در اینجا، هر هفته یک مسئله ریاضی قرار داده میشود. میتوانید راهحلهایتان را برای ما ارسال کنید. همچنین، میتوانید راهحل بقیهٔ کاربران را نیز ببینید و با آنها دربارهٔ این مسائل گفتوگو کنید.
اگر هیچیک از کابران پاسخ درستی برای یک مسئله نفرستاده باشند، مسئلههای هفتههای بعدی روی سایت قرار داده نمیشود.
هفتهٔ بیستوششم
مسئلهٔ هشت وزیر. چگونه \(8\) وزیر را در یک صفحهٔ شطرنج قرار دهیم به طوریکه هیچکدام دیگری را تهدید نکند.

هفتهٔ بیستوپنجم
در مسئلهٔ هفتهٔ بیستوچهارم نمونهای از مسائل عبور از رودخانه را دیدید. این هفته چندین مسئله مشابه با مسئلهٔ هفتهٔ قبل را مطرح میکنیم. همچنین ویدئویی از یکی از اساتید ریاضی دربارهٔ مسئلهٔ عبور از رودخانه آمده است. در انتهای این ویدئو یک مسئلهٔ حلنشده و جایزهدار مطرح میشود.

هفتهٔ بیستوچهارم
سه آدم و سه آدمخوار کنار رودخانهای ایستادهاند. یک قایق، با ظرفیت \(2\) نفر، برای حمل آنها وجود دارد. اگر در یک طرف رودخانه، تعداد آدمها کمتر از تعداد آدمخوارها باشد، آدمخوارها آدمها را میخورند. چگونه این شش نفر به طرف دیگر رودخانه بروند بهطوری که هیچ آدمی خورده نشود؟

هفتهٔ بیستوسوم
مسئلهٔ اول. حمید کنار یک رودخانه ایستاده است. او یک ظرف \(7\) لیتری و یک ظرف \(5\) لیتری دارد. آیا او میتواند فقط با استفاده از این دو ظرف، \(6\) لیتر آب از رودخانه بردارد؟

مسئلهٔ دوم. سه پیمانه به گنجایش \(8\)، \(5\)، و \(3\) لیتر داریم و پیمانهٔ \(8\) لیتری پر از شربت است. چگونه میتوانیم تنها با استفاده از این سه پیمانه، \(8\) لیتر شربت را به دو قسمت مساوی تقسیم کنیم؟
مسئلهٔ سوم. نسرین یک پیمانهٔ \(7\) لیتری و یک پیمانهٔ \(13\) لیتری که هر دو پر از شیر هستند، دارد. او یک پیمانهٔ \(19\) لیتری خالی هم دارد. آیا نسرین فقط با استفاده از این سه ظرف میتواند \(10\) لیتر شیر برای دوستش اندازه بگیرد؟
هفتهٔ بیستودوم
سه تا آجر هماندازه و یک قرقرهٔ نخ داریم. میخواهیم فقط با استفاده از این سه آجر (و بدون استفاده از هیچ فرمولی مثل رابطهٔ فیثاغورس یا …) نخی بهاندازهٔ طول قطر آجر بِبُریم. چگونه چنین کاری را انجام دهیم؟

تعریف قطر مکعبمستطیل. به پارهخطی که دو رأس مکعبمستطیل را که در هیچ وجهی مشترک نیستند، بههم وصل کند، قطر مکعبمستطیل میگویند.

هفتهٔ بیستویکم
چهار نقطه در صفحه رسم کنید که فاصلههای دوبهدو آنها فقط دو عدد مختلف باشند. چند جواب متفاوت وجود دارد؟
برای مثال، یکی از جوابها این است که چهار نقطه، رأسهای یک مربع باشند.

هفتهٔ بیستم
با \(n\) برش، یک پیتزای دایرهای شکل، حداکثر به چند تکه تقسیم میشود؟

برای مثال، اگر \(n=6\)، آنگاه حداکثر تعداد تکههای پیتزا برابر \(22\) است.

هفتهٔ نوزدهم
به دنبالهای از چهار عدد طبیعی، مانند \(a,b,c,d\)، یک دنبالهٔ عجیبوغریب میگوییم هروقت که هر سه دنبالهٔ زیر، دنبالههایی عجیب باشند:
\[\begin{aligned}&a,b,c,d\\&a,b,c\\&b,c,d.\end{aligned}\] (در مسئلهٔ هفتهٔ هجدهم، دنبالهٔ عجیب تعریف شده است.)
چند جفت \((m,n)\) وجود دارد بهطوریکه دنبالهٔ زیر، دنبالهای عجیبوغریب باشد؟
\[m,1176,n,48400\]

هفتهٔ هجدهم
دنبالهای از اعداد طبیعی را یک دنبالهٔ عجیب مینامیم هر وقت دو شرط زیر را داشته باشد.
\(\bullet\) هریک از عددهای دوم به بعد دنباله، از عددی قبلی بزرگتر باشند.
\(\bullet\) حاصلضرب همهٔ جملههای دنباله، مربع کامل باشد.
برای مثال، دنبالهٔ \[2,6,27\] یک دنبالهٔ عجیب است؛ زیرا \(6>2\)، \(27>6\)، و \[2\times6\times27=324=18^2.\]بیشترین تعداد اعدادی که میتوان از بین اعداد \(1\)، \(2\)، \(3\)، \(\dots\)، و \(12\) انتخاب کرد و با آنها یک دنبالهٔ عجیب ساخت، چند عدد است؟

هفتهٔ هفدهم
مطابق مراحل زیر، میتوان به هر پارهخط یک دستانداز اضافه کرد:
مرحلهٔ اول. پارهخط را به سه قسمت مساوی تقسیم میکنیم.
مرحلهٔ دوم. یک مثلث متساویالاضلاع روی پارهخط میانی میسازیم.
مرحلهٔ سوم. پارهخط میانی را حذف میکنیم.
در شکل زیر، سه مرحلهٔ بالا روی پارهخطی به طول \(3\) اجرا شده است.
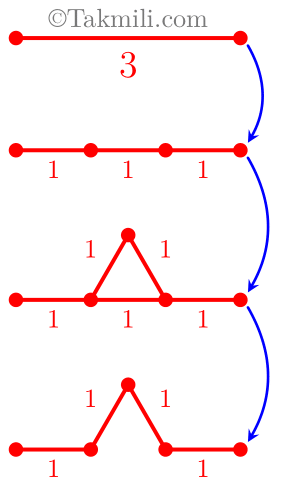
آرمیتا روی یک پارهخط به طول \(n\) یک دستانداز ایجاد کرد و مسیر ساخته شده را مسیر ۱ نامید. سپس روی هریک از پارهخطهای مسیر ۱ یک دستانداز ایجاد کرد و مسیر ساخته شده را مسیر ۲ نامید. او همین کار را تکرار کرد تا مسیر ۳، مسیر ۴، و مسیر ۵ ساخته شوند. اگر \(n\) عددی طبیعی بوده باشد و طول مسیر ۵ نیز عددی طبیعی شود، آنوقت کمترین مقدار ممکن برای \(n\) چیست؟
در شکل زیر، مسیر ۱ و مسیر ۲ آرمیتا نشان رسم شده است.

هفتهٔ شانزدهم
الگوی عددی زیر را ببینید:

اگر الگوی بالا را ادامه دهیم، قطر اول این الگو، دنبالهٔ\[1,2,3,4,5,6,\dots\]است که از $1$ شروع میشود و هر عدد یک واحد از عدد قبلی بزرگتر است. قطر دوم این الگو، دنبالهٔ\[2,4,6,8,10,\dots\]است که از $2$ شروع میشود و هر عدد دو واحد از عدد قبلی بزرگتر است. بههمینترتیب، قطر $n$اُم این الگو با عدد $n$ شروع میشود و هر عدد $n$ واحد از عدد قبلی بزرگتر است.
عدد \(1400\) برای اولینبار در چندمین سطر افقی این الگو ظاهر میشود؟
هفتهٔ پانزدهم
در شکل زیر، معنای بردارهای قرمز و آبی بهترتیب جمع و ضرب است. و دایرههای خالی باید با اعداد طبیعی متفاوت پر شوند. دایرهٔ زردرنگ را با چه عدد (عددهایی) میتوان پر کرد؟ (همهٔ جوابهای ممکن را بیابید.)

هفتهٔ چهاردهم
شکل زیر را در نظر بگیرید.

میخواهیم چند خط راست رسم کنیم بهطوریکه از درون هر مربع کوچک شکل بالا، دستکم یک خط گذشته باشد. کمترین تعداد این خطها چندتاست؟ شکلی رسم کنید که نشان دهد این تعداد خط کافی است.
هفتهٔ سیزدهم
یک مکعبمستطیل توپُر \(8\times8\times n\)، از مکعبهای \(1\times1\times1\) ساخته شده است. فرض کنید \(A\) مساحت کل مکعبمستطیل، و \(B\) مجموع مساحت کل مکعبهای \(1\times1\times1\) سازندهٔ مکعبمستطیل باشد. همهٔ \(n\)هایی را پیدا کنید که برای آنها، \(\frac{B}{A}\) عددی طبیعی باشد.
راهنمایی: شکل زیر، مثالی است که در آن \(n=5\). در این مثال، \(\frac{B}{A}\) عددی طبیعی نیست!

هفتهٔ دوازدهم
در چهارضلعی \(ABCD\)، دو قطر \(AC\) و \(BD\) یکدیگر را در نقطهٔ \(E\) قطع کردهاند. میدانیم سه پارهخط \(AB\)، \(BC\)، و \(BD\) برابرند و اندازهٔ زاویهٔ \(CBD\) دو برابر اندازهٔ زاویهٔ \(DBA\) است.

دوازده زاویهٔ داخلی مثلثهای \(AEB\)، \(BEC\)، \(CED\)، و \(DEA\) را در نظر بگیرید. اگر اندازهٔ همهٔ این دوازدهتا زاویه، برحسب درجه، اعدادی صحیح باشند، و بدانیم اندازهٔ دقیقاً ششتا از این زاویهها، برحسب درجه، عددی اول است، آنوقت همهٔ مقدارهای ممکن برای زاویهٔ \(DCA\) را بهدست آورید.
هفتهٔ یازدهم
با هشتتا \(8\) و با استفاده نمادهای جمع، تفریق، ضرب، تقسیم، توان، رادیکال، فاکتوریل، پرانتز، یا ممیز، عدد \(1000\) را بسازید.
برای مثال، در تقویم ریاضی این ماه سایت تکمیلی (که در نوار پایینی سایت موجود است)، در روز هشتم دی، اینکار فقط با استفاده از عمل جمع انجام شده بود:

یک مثال دیگر:
\[\begin{aligned}&888+(8+8)\times8-8-8=1000.\end{aligned}\]
آیا میتوانید چند روش دیگر برای این کار ارائه کنید؟
هفتهٔ دهم
مسیری به طول \(14\) متر شامل هفت ناحیهٔ یکمتری آبی، و هفت ناحیهٔ یکمتری قرمز است. ناحیههای آبی و قرمز، یکیدرمیان هستند. چرخی دایرهای به شعاع \(2\) متر بهصورت زیر در ابتدای مسیر قرار داده شده است. این چرخ به چهار ناحیهٔ برابر تقسیم شده است: دو ناحیهٔ آبی و دو ناحیهٔ قرمز.

وقتی چرخ دقیقاً یک دور کامل بچرخد (در جهت نشان داده شده در شکل بالا)، در چند درصد از مسیری که طی میکند، ناحیهٔ قرمز چرخ، ناحیهٔ قرمز مسیر را لمس میکند؟
هفتهٔ نهم
پینوکیو ادعا میکند که خطی راست رسم کرده است که همهٔ ضلعهای (و نه رأسهای) یک \(1001\)ضلعی را قطع کرده است. آیا ادعای پینوکیو درست است؟ چرا؟

هفتهٔ هشتم
در شکل زیر، زاویههای سبز برابرند و پارهخطهای قرمز موازیاند. با توجه به اندازهٔ زاویههای داده شده، اندازهٔ زاویههای سبز چند درجه است؟

هفتهٔ هفتم
در جدول زیر، بهجای کدام اعداد صفر قرار داده شود تا مجموع هر سطر و هر ستون برابر \(16\) شود؟ برای اینکار، حداقل چندتا صفر لازم است؟

هفتهٔ پنجم
در شکل زیر، اندازهٔ یکی از زاویهها مشخص شده است، و زاویههای همرنگ برابرند. زاویهٔ آبی چند درجه است؟

هفتهٔ چهارم
در شکل زیر، معنای بردارهای قرمز و آبی بهترتیب جمع و ضرب است. و دایرههای خالی باید با اعداد صحیح پر شوند. دایرهٔ زردرنگ را با چه عدد (عددهایی) میتوان پر کرد؟

هفتهٔ سوم
روی وجههای یک مکعب، اعداد \(1\) تا \(6\) نوشته شدهاند. گستردهٔ این مکعب بهصورت زیر است.

سپیده تعدادی از مکعبهای بالا را بهصورت زیر بههم چسبانده و آنها را با وضعیت زیر، روی یک میز گذاشته است بهطوریکه مجموع عددهای نوشته شده روی وجههایی که دیده میشوند، حداکثر مقدار ممکن باشد. این مقدار را بهدست آورید.
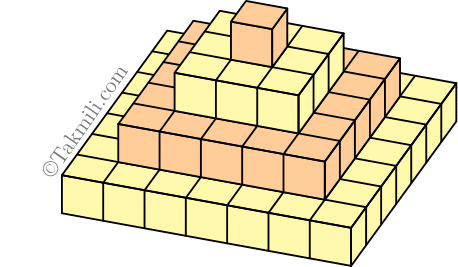
هفتهٔ دوم
شکل زیر، یک مربع است. میدانیم، همهٔ زاویههای شکل زیر قائمه هستند، طول چهار پارهخط قرمز برابر است، و مساحت ناحیههای زرد و سبز بهترتیب \(20\) و \(36\) است. مساحت کل مربع داده شده چقدر است؟

هفتهٔ اول
ابتدا قانون دنبالهٔ زیر را کشف کنید. \[1,1,4,9,25,64,\dots\] سپس، سعی کنید روش هوشمندانهای برای جمع زدن جملههای اول تا نهم این دنباله بیابید.