مثلث خیام پاسکال (هفتم. فصل ۱. مسئله‌ها. تمرین ۲۴)

۷. ۱. ۱. ۲۴. مجلهٔ Notices که انجمن ریاضی آمریکا آن را چاپ می‌کند، در یکی از شماره‌هایش، یک الگوی عددی معروف را به‌عنوان تصویر روی جلد انتخاب کرده است.

ابتدا الگوی عددی بالا را به‌دقت مشاهده و قانونِ آن را کشف کنید. سپس باتوجه‌به قانون الگو، سه ستون به سمت چپ آن اضافه کنید.

راهنمای حل

ستون اول، دو عدد دارد، ستون دوم سه عدد دارد، ستون سوم چهار عدد دارد، و به‌همین‌‌ترتیب تعداد اعداد هر ستون یکی بیشتر از شمارهٔ آن ستون است.
اولین و آخرین عدد هر ستون ۱ است؛ عدد دوم هر ستون، مجموع عدد اول و دوم ستون قبل است. عدد سوم هر ستون، مجموع عدد دوم و سوم ستون قبل است. عدد چهارم هر ستون، مجموع عدد سوم و چهارم ستون قبل است. و با همین قانون اعداد دیگر هر ستون نوشته می‌شوند.
سه ستون بعدی این جدول به‌صورت زیر هستند.
\[\begin{matrix}1&1&1\\15&14&13\\105&91&78\\455&364&286\\1365&1001&715\\3003&2002&1287\\5005&3003&1716\\6435&3432&1716\\6435&3003&1287\\5005&2002&715\\3003&1001&286\\1365&364&78\\455&91&13\\105&14&1\\15&1&\\1&&\\\end{matrix}\]

این جدول در کتاب‌های غربی، مثلث پاسکال نامیده شده است. بلز پاسکال، ریاضیدان فرانسوی در قرن هفدهم میلادی می‌زیسته است. او اعداد مثلث را به‌صورت زیر نوشته است:

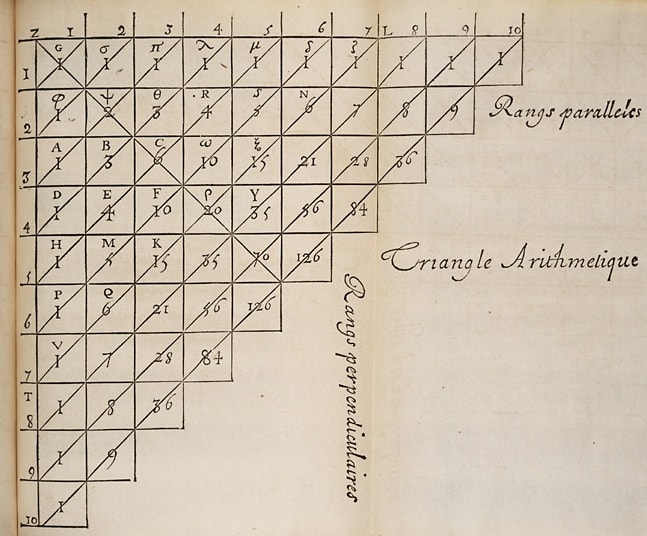
در ریاضیات، قضیه‌ها و الگوها معمولاً به نام کسی ثبت می‌شود که اولین‌بار آن قضیه یا الگو را کشف کرده است. مطمئناً پاسکال اولین کسی نیست که الگوی بالا و خواص آن را کشف کرده باشد.

دو قرن قبل از میلاد مسیح، یک ریاضیدان هندی به نام پینگالا خاصیت‌هایی از اعداد این مثلث را کشف کرده است.

در قرن دهم میلادی، یک ریاضیدان ایرانی به نام کرجی در کتابی مثلث بالا را توصیف کرده است. حدود ۱۰۰ سال پس از کرجی، عمر خیام، ریاضیدان، شاعر، و منجم ایرانی، خواص بیشتری از این الگوی عددی را کشف می‌کند. در ایران این الگوی عددی به مثلث خیام مشهور است.

این الگوی عددی در چین به مثلث یانگ هویی مشهور است. یانگ هویی ریاضیدانِ قرن سیزدهم میلادی است که اعداد مثلث را به‌صورت زیر نوشته است:

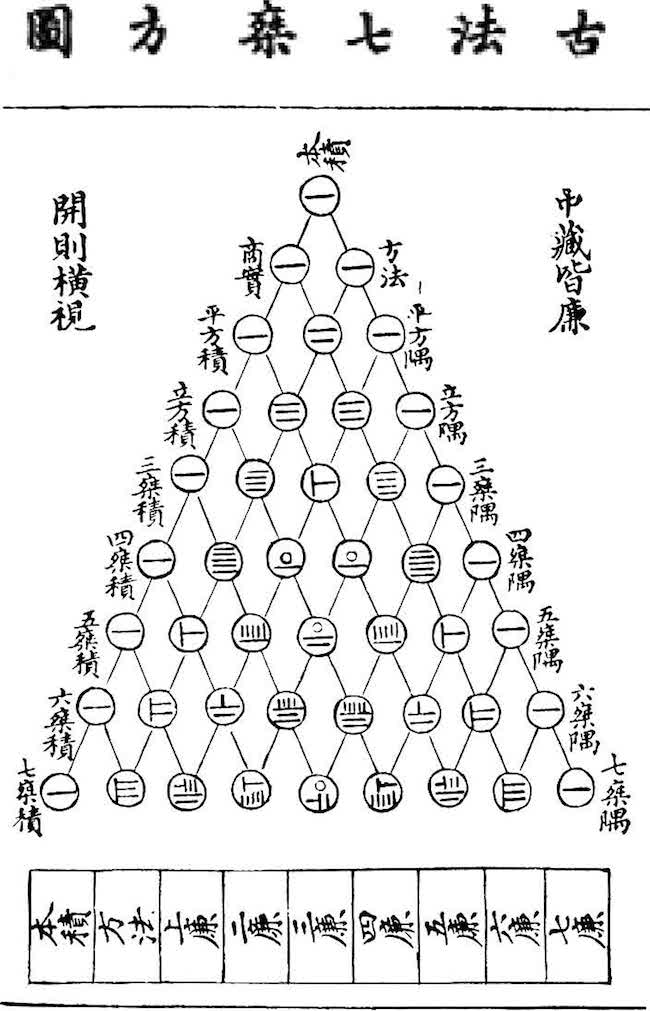
ایزاک نیوتن، تعمیم‌ رابطه‌هایی از اعداد این الگو را کشف کرده است. در بعضی از کتاب‌ها، اعداد این الگو «ضرایب دوجمله‌ای نیوتن» نامیده شده‌اند. نیوتن در قرن هفدهم و هجدهم میلادی می‌زیسته است.

در صفحهٔ ۱۴۹۸، شمارهٔ ۱۱ جلد ۶۰ مجلهٔ ریاضی انجمن ریاضی آمریکا دربارهٔ تصویر روی جلد آن (تصویری که در صورت این مسئله می‌بینید) نوشته شده است:

در صفحهٔ بالا نوشته شده است که تصویر روی جلد را یک ریاضیدان مسلمان به‌نام السماوال در سن ۱۹ سالگی نوشته است. او در سال ۱۱۳۰ میلادی در بغداد متولد شد. السماوال نوشته‌های کرجی را خوانده بود.

همان‌طور که در تصویر مجلهٔ انجمن ریاضی آمریکا می‌بینید، اعداد این مثلث در مقاله‌ها و کتاب‌های جدید «ضرایب دوجمله‌ای» (Binomial Coefficient) نامیده می‌شوند.

ویدئوی زیر نیز دربارهٔ مثلث عددی خیام است. تمامی حقوق این ویدئو متعلق به TED-Ed است و شرکت زنجیره ابتکارات ما (ZEM) آن را دوبله کرده است.