۸. ۱. ۱. ۸. به الگوی زیر توجه کنید.

الف) شکل پنجم این الگو را رسم کنید.
ب) در شکل بیستم این الگو، چند گلوله وجود دارد؟ این تعداد با عددی که در قسمت «ب» مسئلۀ قبل بهدست آوردید، چه رابطهای دارد؟
ج) با توجه به شکلهای صفحه قبل و شکلهای مسئلۀ قبل، حاصل عبارت زیر را بهدست آورید.
\[1+2+3+\cdots+51\]
راهنمای حل
الف)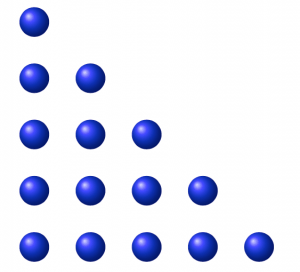
ب) تعداد گلولههای شکل اول این الگو یکی است.
تعداد گلولههای شکل دوم این الگو برابر است با:
\[1+2=3\]
تعداد گلولههای شکل سوم این الگو برابر است با:
\[1+2+3=6\]
تعداد گلولههای شکل چهارم این الگو برابر است با:
\[1+2+3+4=10\]
بنابراین، تعداد گلولههای شکل بیستم این الگو برابر با حاصل عبارت زیر است.
\[1+2+3+\cdots+20\]
حال میخواهیم با استفاده از مسئلۀ قبل، روشی برای محاسبهٔ حاصل عبارت بالا بیابیم.
باتوجهبه اینکه تعداد گلولههای هریک از شکلهای این الگو، نصف تعداد گلولههای شکل متناظر با آن، در الگوی مسئلۀ قبل است (شکلهای زیر را ببینید.)، پس کافی است نصف تعداد گلولههای شکل بیستم الگوی مسئلۀ قبل را بهدست آوریم.
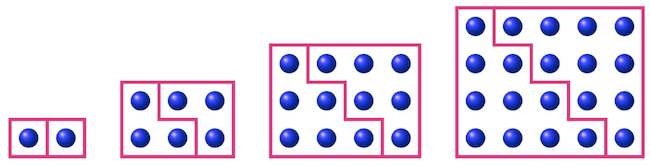
بنابراین تعداد گلولههای شکل بیستم را میتوان اینگونه بهدست آورد:
\[\begin{aligned}1+2+3+\cdots+20&=\frac{20\times 21}{2}\\&=10\times 21\\&=210.\end{aligned}\]
ج) باتوجهبه آنچه در قسمت قبل گفته شد، داریم:
\[\begin{aligned}1+2+3+\cdots+51&=\frac{51\times 52}{2}\\&=51\times 26\\&=1326.\end{aligned}\]
یک ایراد در صورت مسئله. بهتر بود زیر هر شکل، شمارهٔ شکل نوشته میشد. ما فرض کردیم ترتیبِ شمارهگذاریِ شکلها از چپ به راست باشد. اگر شخص دیگری فرض کند ترتیبِ شمارهگذاریِ شکلها از راست به چپ است، آنوقت شکل پنجم چگونه خواهد بود؟
پرسش در کلاس ۱. حاصل عبارت زیر را بهدست آورید.
\[1+2+3+\cdots+1000\]
پرسش در کلاس ۲. به اعداد دنبالهٔ زیر (تعداد گلولههای شکلهای مسئلهٔ بالا)، اعداد مثلثی میگویند.
\[1,3,6,10,15,21,\cdots\]
الف) چند عدد مثلثی کوچکتر از ۲۰۰ وجود دارد؟ همهٔ آنها را بنویسید.
ب) چند عدد مثلثی کوچکتر از ۱۰۰۰ وجود دارد که بر ۱۷ بخشپذیر باشد؟ همهٔ آنها را بنویسید.
ج) حاصل جمع دو عدد مثلثی ۶ و ۱۵ برابر با یک عدد مثلثی دیگر است:
\[6+15=21\]
آیا میتوانید چند جفت عدد مثلثی دیگر پیدا کنید که حاصلجمع آنها یک عدد مثلثی باشد؟
د) آیا میتوانید سه عدد مثلثی بیابید که مجموع آنها یک عدد مثلثی دیگر باشد؟


ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️در واقع تعمیم قسمت د میشه که ما بی شمار گروه n تایی از اعداد مثلثی را داریم که جمعشان هم عدد مثلثی است
برای بی شمار بودن تعداد جفت هایی که جمعشان عدد مثلثی است و خودشان نیز عدد مثلثی اند !
فاصله هر دو عدد مثلثی :
2/(n+1)(n+2) و 2/n(n+1)
با کمی جبر و فاکتور گیری بدست می اید : n+2
و چون می تواند عدد مثلثی باشد از این رو دلیلی دیگری داریم
2 ) ج
45+10=55
15+105=120
36+55=91
45+21=66
15+21=36
در واقع بی شمار جفت داریم ! چون هر عدد مثلثی در فاصله بین دو عدد مثلثی معین ظاهر می شود در نتیجه بی شمار جفت داریم
فاصله دو عدد مثلثی عددی طبیعی است و چون عدد مثلثی هم عضو ان است در واقع باز بی شمار جفت داریم
د) بله!
1+3+6=10
1+6+21=28
6+10+120=136
1+15+120=136
10+3+78=91
باز مثل دفعه قبل هر جفت رو می سازیم بعد بالاخره در فاصله ها عدد مثلثی بروز میکنه پس در واقع بی شمار سه تایی هم داریم !
جواب پرسش
1= بدیهیه که میشه 1000 ضربدر 1001 تقسیم به دو ( کتاب تکمیلی هشتم هم یه روش توضیح داده ! )
پس 500500 مجموع می شود
2 الف )
ابتدا بزرگترین مثلثی را پیدا میکنیم که به این گونه است : 200> n(n+1)/2
حال : 400>n(n+1)
می دانیم اگر 20 ضربدر20 داشتیم حاصل مساوی 400 بود پس 19 بزرگترین مقدار n است
کمترین مقدار n هم که 1 است
پس مجموعا 19 عدد داریم
1.3.6.10.15.21.28.36.45.55.66.78.91.105.120.136.153.171.190
عدد بعدی 210 است که بزرگتر از 200 است پس 19 عدد داریم
ب ) ابتدا برسی میکنیم که بزرگترین عدد مثلثی کوچکتر از هزار چیست ؟
1000>n(n+1)/2
2000>n(n+1)
رادیکال 2000 تقریبا 44 است پس 44 بزرگترین مقدار n است هم چنین واضح است بزرگترین مقدار n+1 برابر با 44 است
حال مضارب 17 زیر n و n+1 :
17-34
حال یا خود n مضرب 17 است یا یکی بیشتر از ان پس در مجموع دو ضربدر دو یعنی 4 عدد خاصیت خواسته شده را دارند
136-153-561-595
ولی من احساس میکنم جواب این نمیشه
از روش گاوس میریم:1+2+3+……+20=
20*21تقسیم بر 2 = 210 جمعشون میشه
منظورتون جواب قسمت «ب» است؟!!
الف ۱۹
ب ۴۴ تا کمتر از ۱۰۰۰ هست دربین آنها دو تاش بر ۱۷ هم بخش پذیرهست
د۱,۳,۶
سوال ها تون خیلی خوب و جالب و آموزنده است ممنون برای سوال ها تون کاش برای درس های دیگر هم نمونه سوال های تکلمیلی رو داشتین
اینها برای کتاب تکمیلی بچهای تیز هوشانه از جمله خودم