گزینهٔ ۲ درست است.
این مسئله، مشابه تمرین ۲۰ صفحهٔ ۱۰۱ کتاب ریاضیات تکمیلی هشتم، و همچنین مشابه تمرین ۷ صفحهٔ ۵۶ و تمرین ۱۵ صفحهٔ ۵۹ کتاب ریاضیات تکمیلی نهم است.
تمرین ۲۰ صفحهٔ ۱۰۱ (هشتم)
۸. ۶. ۳. ۲۰. در شکل زیر، $\widehat{B}=120^\circ$ و مثلث $ACD$ متساویالاضلاع است.

ثابت کنید:
الف) پارهخط $BD$ نیمساز زاویهٔ $B$ است.
ب) $BD=AB+BC$.
راهنمایی: $BC$ را از طرف $B$ به اندازهٔ $AB$ امتداد دهید و نقطه انتها را $E$ بنامید. سپس ثابت کنید دو مثلث $ABD$ و $AEC$ همنهشتاند.
راهنمای حل
همانطور که در راهنماییِ مسئله گفته شده است عمل کنیم. در زیر، شکلِ راهحل را دوبار رسم کردهایم تا مثلثهایی که میخواهیم همنهشتیِ آنها را ثابت کنیم، واضحتر دیده شوند.


مثلث $ABE$ متساویالاضلاع است. (چرا؟)
چون ضلع $BE$ را برابر با $AB$ رسم کردهایم، پس مثلث $ABE$ متساویالساقین است. از طرفی چون $A\widehat{B}C=120^\circ$، پس $A\widehat{B}E=60^\circ$. یعنی مثلث $ABE$ مثلثی متساویالساقین است که یک زاویهٔ آن $60$ درجه میباشد؛ پس دو زاویهٔ دیگر این مثلث نیز ۶۰ درجه است و در نتیجه $ABE$ متساویالاضلاع میباشد.
دو مثلث $ABD$ و $AEC$ در حالت ضزض همنهشتاند. زیرا:
۱. $AD=AC$؛ چون هر دو ضلع مثلث متساویالاضلاع $ACD$ هستند.
۲. $AB=AE$؛ چون هر دو ضلع مثلث متساویالاضلاع $ABE$ هستند.
۳. $D\widehat{A}B=C\widehat{A}E$. (چرا؟)
.
باتوجهبه تساویهای
\[\begin{aligned}D\widehat{A}B&=D\widehat{A}C+C\widehat{A}B\\C\widehat{A}E&=B\widehat{A}E+C\widehat{A}B.\end{aligned}\]
کافی است ثابت کنیم $D\widehat{A}C=B\widehat{A}E$ و این تساوی برقرار است؛ چون دو زاویهٔ $D\widehat{A}C$ و $B\widehat{A}E$ بهترتیب زاویههای مثلثهای متساویالاضلاع $ACD$ و $ABE$ هستند. پس اندازه هریک برابر ۶۰ است.
در بقیهٔ اجزای متناظرِ دو مثلث $ABD$ و $AEC$ به دست میآید:
۱. $A\widehat{B}D=A\widehat{E}C=60^\circ$؛ یعنی $BD$ نیمساز زاویهٔ $ABC$ است(؟).
۲. $BD=EC$؛ یعنی $BD=AB+BC$ (؟).
برای معلمان. این تمرین مشابه تمرینهای ۹. ۳. ۵. ۱۵ و ۹. ۳. ۵. ۷ است. اینکه دانشآموز ارتباط بین تمرینهای مشابه را بفهمد بسیار مهم است.
تمرین ۷ صفحهٔ ۵۶ (نهم)
۹. ۳. ۵. ۷. سه نقطهٔ $A$، $B$ و $C$ دایرهای را به سه کمان برابر تقسیم کردهاند و $M$ نقطهای دلخواه روی کمان $AC$ است. ثابت کنید وتر $MB$ با مجموع وترهای $MA$ و $MC$ برابر است.
راهنمای حل
سه کمان $AB$، $AC$، و $BC$ برابرند. پس:
\[\overset{\frown}{AB}=\overset{\frown}{AC}=\overset{\frown}{BC}=\frac{360^\circ}{3}=120^\circ.\quad (1)\]
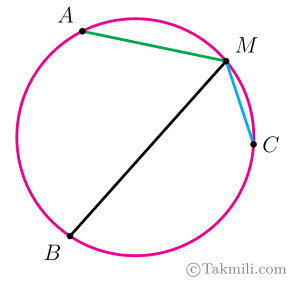
بنابراین:
\[A\widehat{M}B=C\widehat{M}B=60^\circ.\quad (2)\]
(چرا؟)
زاویههای $AMB$ و $CMB$ زاویههای محاطی هستند. پس بنابه قضیهٔ زاویهٔ محاطی و رابطهٔ $(1)$ داریم:
\[\begin{aligned}A\widehat{M}B=\frac{\overset{\frown}{AB}}{2}=60^\circ,\\C\widehat{M}B=\frac{\overset{\frown}{BC}}{2}=60^\circ.\end{aligned}\]
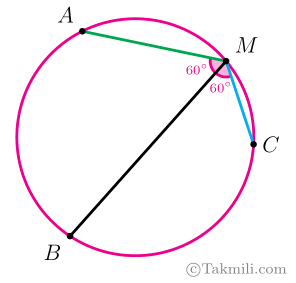
وتر $CM$ را (از طرف $M$) بهاندازهٔ $MA$ امتداد میدهیم تا نقطهٔ $D$ بهدست آید. مثلث $AMD$ متساویالاضلاع است. (چرا؟)
بنابه رابطهٔ $(2)$ اندازهٔ زاویهٔ $AMC$ برابر $120$ درجه است. چون زاویهٔ $DMA$ مکمل زاویهٔ $AMC$ است، پس:
\[D\widehat{M}A=60^\circ.\]
چون $MA$ و $MD$ برابرند و اندازهٔ زاویهٔ $DMA$ برابر ۶۰ درجه است، پس مثلث $ADM$ مثلثی متساویالساقین است که یک زاویهٔ ۶۰ درجه دارد. بنابراین مثلث $ADM$ متساویالاضلاع است.
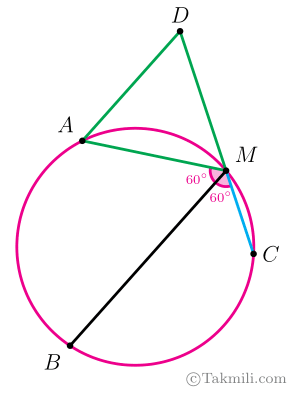
بنابراین، دو مثلث $ABM$ و $ACD$ همنهشت هستند. (چرا؟)
چون $AD$ و $AM$ ضلعهای مثلث متساویالاضلاع $ADM$ هستند، پس:
\[AD=AM.\quad(3)\]
بنابه رابطهٔ $(1)$ کمانهای $AB$ و $AC$ برابرند. پس بنابه قضیهٔ کمان و وتر، وترهای نظیر این دو کمان نیز برابرند. یعنی:
\[AC=AB.\quad (4)\]
در مثلث متساویالاضلاع $ADM$ زاویهٔ $DAM$ برابر ۶۰ درجه است. از طرفی، بنابه رابطهٔ $(1)$ و قضیهٔ زاویهٔ محاطی، زاویهٔ $BAC$ نیز برابر ۶۰ درجه است.
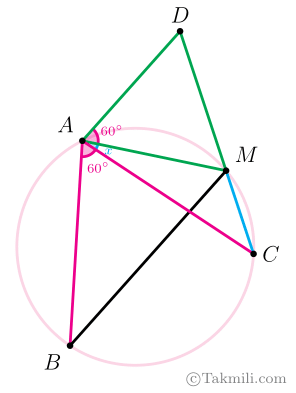 پس همانطور که در شکل بالا میبینید،
پس همانطور که در شکل بالا میبینید،
\[C\widehat{A}D=B\widehat{A}M=60^\circ+x.\quad (5)\]
از رابطههای $(3)$، $(4)$، و $(5)$ نتیجه میشود که دو مثلث $ABM$ و $ACD$ در حالت ضزض همنهشت هستند.
در نتیجه:
\[\begin{aligned}&CD=BM\\&\Rightarrow CM+MD=BM\\&\Rightarrow CM+MA=BM.\end{aligned}\]
راهنمای حل (۲)
نقشهٔ راه. نقطهٔ \(N\) را طوری روی \(MB\) انتخاب میکنیم که \(MN=MC\). در نتیجه مثلث \(CMN\) متساویالاضلاع است. حال میتوان ثابت کرد که دو مثلث \(ACM\) و \(BCN\) در حالت ززض همنهشتاند. پس \(BN=AM\) و در نتیجه \(AM+CM=BM\).
برای معلمان. این تمرین مشابه تمرینهای ۸. ۶. ۳. ۲۰ و ۹. ۳. ۵. ۱۵ است. اینکه دانشآموز ارتباط بین تمرینهای مشابه را بفهمد بسیار مهم است.
تمرین ۱۵ صفحهٔ ۵۹ (نهم)
۹. ۳. ۵. ۱۵. در مثلث $ABC$، $\widehat{A}=120^\circ$. روی نیمساز زاویهٔ $A$ نقطهٔ $D$ طوری انتخاب شده است که $AD=AB+AC$. اندازهٔ زاویههای مثلث $BDC$ چقدر هستند؟
راهنمای حل
ضلع $AC$ را (از طرف $A$) بهاندازهٔ $AB$ امتداد میدهیم و نقطهٔ حاصل را $E$ مینامیم.

چون بنابه فرض مسئله $B\widehat{A}C=120^\circ$، پس در مثلث $ABE$ داریم:
\[AB=AE, B\widehat{A}E=60^\circ.\]
در نتیجه مثلث $ABE$ متساویالاضلاع است(؟).
دو مثلث $ABD$ و $EBC$ در حالت دو ضلع و زاویهٔ بین همنهشتاند. (چرا؟)
از متساویالاضلاع بودن مثلث $ABE$ داریم $EB=AB$.
چون ضلع $AC$ را به اندازهٔ $AB$ امتداد دادیم پس $EC=AB+AC$. از طرفی بنابه فرض مسئله داریم $AD=AB+AC$. پس $EC=AD$.
چون مثلث $ABE$ متساویالاضلاع است پس $\widehat{E}=60^\circ$. از طرفی بنابه فرض مسئله $AD$ نیمساز زاویهٔ $B\widehat{A}C$ است و $B\widehat{A}C=120^\circ$. بنابراین $B\widehat{A}D=60^\circ$. در نتیجه $\widehat{E}=B\widehat{A}D$.
بنابراین دو مثلث $ABD$ و $EBC$ در حالت دو ضلع و زاویهٔ بین همنهشتاند.
در نتیجه $BC=BD$ و $D\widehat{B}C=60^\circ$. (چرا؟)
در اجزای متناظر دو مثلث همنهشت $ABD$ و $EBC$ داریم $BD=BC$ و
\[\begin{aligned}E\widehat{B}C=A\widehat{B}D&\Longrightarrow E\widehat{B}A+A\widehat{B}C=A\widehat{B}C+D\widehat{B}C\\&\Longrightarrow E\widehat{B}A=D\widehat{B}C.\end{aligned}\]
چون مثلث $ABE$ متساویالاضلاع است پس $E\widehat{B}A=60^\circ$ و در نتیجه $D\widehat{B}C=60^\circ$.
چون $BC=BD$ و $D\widehat{B}C=60^\circ$، پس مثلث $BCD$ متساویالاضلاع است(؟) و هر سه زاویهٔ آن $60$ درجه میباشند.
برای معلمان. این تمرین مشابه تمرینهای ۸. ۶. ۳. ۲۰ و ۹. ۳. ۵. ۷ است. اینکه دانشآموز ارتباط بین تمرینهای مشابه را بفهمد بسیار مهم است.


ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️سلام خسته نباشیدبرای پایه ششمی ها آزمون هدیه شبیه سازی طراحی نشده؟
سلام
ریآزمون تست هوش هم داریم.
از صفحهٔ ریآزمون سایت تکمیلی میتوانید به ریآزمون هوش دسترسی داشته باشید.