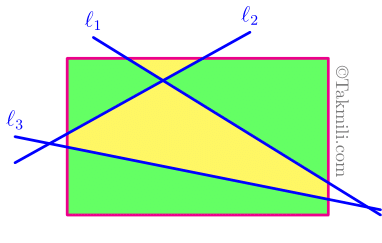
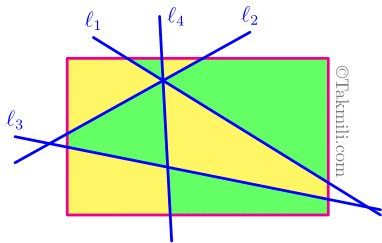
با رسم سه خطّ راست، مستطیل زیر به پنج ناحیه تقسیم شده است. هریک از این ناحیهها یک چندضلعی هستند.

در اینجا، دو چندضلعی را همسایه مینامیم هرگاه این دو چندضلعی، ضلع مشترکی داشته باشند.
میخواهیم با رسم \(12\) خطّ راست، یک مستطیل را به چندتا چندضلعی تقسیم کنیم و سپس چندضلعیهای بهدست آمده را رنگ بزنیم بهطوریکه چندضلعیهایی که همسایهٔ یکدیگر هستند، رنگهای متفاوتی داشته باشند. برای این کار حداقل به چند رنگ نیاز داریم؟
این مسئله، درواقع حالت خیلی خاصی از مسئلهٔ معروف چهاررنگ است. مسئلهٔ چهاررنگ یکی از معروفترین مسائل ریاضیات قرن گذشته بود که هنوز اثباتی ساختاری برای آن پیدا نشده است. برای کسب اطلاعات بیشتر دربارهٔ قضیهٔ چهاررنگ روی لینک زیر، کلیک کنید.
ویدئوی قضیهٔ چهاررنگ و بازی آنلاین چهاررنگ!
چرا خلاقیت ریاضی مهم است؟
در ویدئوی زیر، دکتر علیرضا علیپور (دبیر ریاضی برجستهٔ کشور و نویسندهٔ کتابهای مرجع المپیاد) به سؤالات مهمی دربارهٔ خلاقیت ریاضی با رویکرد آموزش حل مسئله، پاسخ میدهند.کلاسهای خلاقیت ریاضی دکتر علیپور

ارسال کامنت و دیدگاه
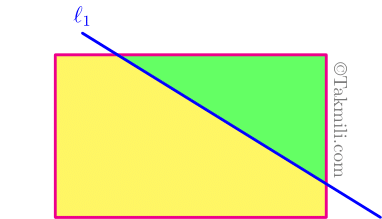
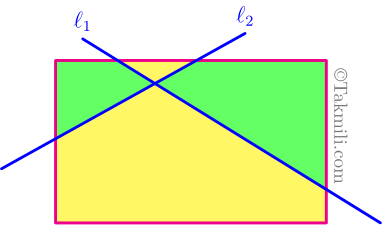
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️هر تعداد خطی که بکشیم، حداقل رنگ مورد نیاز ۲ تا است.
با کشیدن هر خط راست رنگ های یک طرف شکل را معکوس میکنیم
حد اقل با 2 رنگ
حداقل از 2 رنگ
برای شکلی که شما رسم کردهاید، حداقل ۲ رنگ، درست است.
اما در این مسئله میخواهیم راهحلی پیدا کنیم که برای هر حالت ممکن بتوانیم جواب را پیدا کنیم.
یعنی هر جور ۱۲ خط رسم شود، آنوقت حداقل به چند رنگ نیاز داریم. ( در شکل شما، همهٔ خطوط تقریباً موازی همدیگر هستند.)