روی وجه‌های یک مکعب، اعداد \(1\) تا \(6\) نوشته شده‌اند. گستردهٔ این مکعب به‌صورت زیر است.
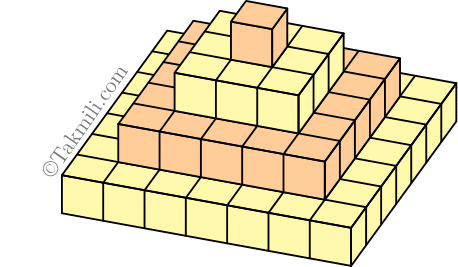
سپیده تعدادی از مکعب‌های بالا را به‌صورت زیر به‌هم چسبانده و آنها را با وضعیت زیر، روی یک میز گذاشته است به‌طوری‌که مجموع عددهای نوشته شده روی وجه‌هایی که دیده می‌شوند، حداکثر مقدار ممکن باشد. این مقدار را به‌دست آورید.
این مسئله را به‌روش‌های مختلفی می‌توان حل کرد. لطفاً از راه‌حل‌تان عکس بگیرید و آن را در قسمت کامنت‌های زیر آپلود کنید. اگر با روش آپلود عکس آشنایی ندارید، در صفحهٔ پرسش‌های متداول سایت تکمیلی، بخش کامنت‌گذاری را بخوانید.
در وب‌سایت تکمیلی، هر هفته یک مسئلهٔ جدید منتشر می‌‌شود. برای مشاهدهٔ مسائل هفته‌های دیگر، روی لینک زیر کلیک کنید.
امکان دارد در جمع یا محاسبه آنها مشکل وجود داشته باشد ولی روش کاملا از نظر بنده درست می باشد. البته فکر می کنم.
در تمام ردیف ها ۳ نوع مکعب وجود دارد.
سعی میکنیم تعداد آنهارا در هر ردیف بدست بیاوریم. الگویی هم بین آنها وجود دارد.
سلام
جواب سوال هفته سوم: 596
کتاب Et عالیه و خیلی خوبه و مباحث را کامل توضیح داده
چه ارتباطی به این مسئله دارد؟!
با سلام. و خسته نباشید جواب من 596 هست.
11=(5+6) 15=(6+4+5) 20=(6+5+4+3+2)
تعداد مکعب هایی که دو وجه شان دیده می شود: 36
تداد مکعب هایی که سه وجه شان دیده می شود: 12
تعداد مکعب هایی که 5 وجه شان دیده می شود: 1
180=12*15 20=1*20 396=11* 36
596=369+20+180
من 596 بدست آوردم ?
با سلام
جواب
باسلام
پاسخ سوال
سلام جوابش ۵۹۶ است
با سلام
جواب سؤال
ببخشید مکعب های پشت تصویر هم حساب میشد؟
بله. فکر کنید همین شکل را روی یک میز گذاشته‌اید و از اطراف به آن نگاه می‌کنید. یعنی وجه‌های که روی میز قرار دارند، و وجه‌هایی که به‌هم چسبیده‌اند، دیده نمی‌شوند.
خب الان سطح پایینیش معلوم نیست نمیدونیم تو خالیه؟ صافه؟ خبر نداریم .
من بخاطر همون سطح پایینی رو نادیده در نظر گرفتم که در این صورت میشه 596
تو خالی یعنی چی؟! همهٔ مکعب‌ها از نوعی هستند که گستردهٔ آن رسم شده است.
منظورم اینه که شاید اگه وجهی رو که روی میزه نگاه کنیم وسطا مکعب وجود نداشته باشه که البته توضیح بالا رو خوندم متوجه شدم ممنون?