مطالب تدریس شده در کلاس
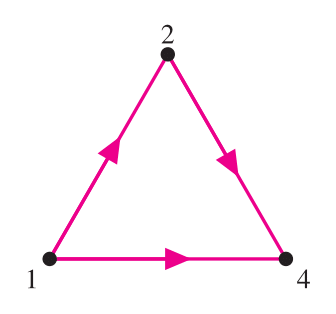
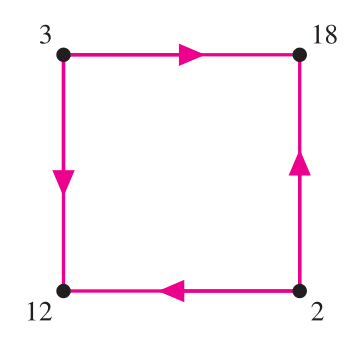
- در چند تا از شکلهای داده شده میتوان با قرار دادن پیکان بهجای تمام پارهخطهای کشیده شده، و قرار دادن تعدادی عدد طبیعی بر تمام رأسها، آن را تبدیل به نموداری کرد که اگر از $a$ به $b$ یک پیکان باشد، آنگاه $a$ شمارندهای از $b$ باشد و برعکس؟
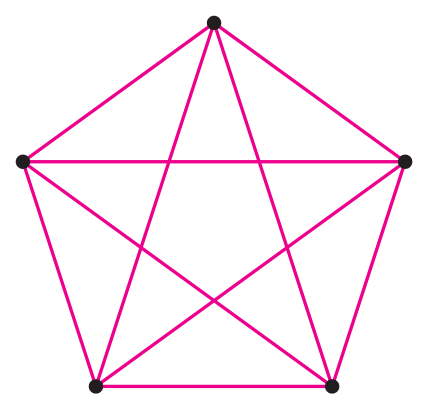
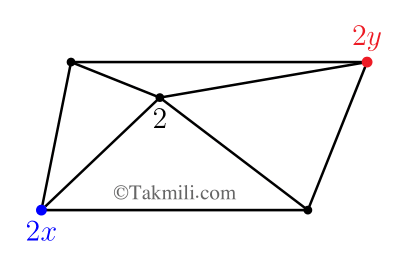
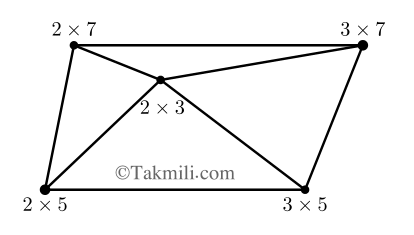
- در شکل زیر، برای هر نقطه یک عدد در نظر گرفتهایم و هر دو نقطهای که بمم آنها غیر از یک است را بههم وصل کردهایم. کوچکترین عددی که میتوان برای نقطهٔ \(A\) در نظر گرفت، چند است؟
- صد لامپ را با شمارههای \(1\) تا \(100\) شمارهگذاری کردهایم. هر لامپ یک کلید دارد که با فشار دادن آن، لامپ روشن یا خاموش میشود. در ابتدا همهٔ لامپها خاموش بودند. صد دیوانه، کلید لامپها را بهصورت زیر فشار دادند.
دیوانهٔ اول کلید همهٔ لامپهای مضرب \(1\) را \(1\)بار فشار داد.
دیوانهٔ دوم کلید همهٔ لامپهای مضرب \(2\) را \(2\)بار فشار داد.
دیوانهٔ سوم کلید همهٔ لامپهای مضرب \(3\) را \(3\)بار فشار داد.
دیوانهٔ چهارم کلید همهٔ لامپهای مضرب \(4\) را \(4\)بار فشار داد.
\(\quad\vdots\)
دیوانهٔ صدم کلید همهٔ لامپهای مضرب \(100\) را \(100\)بار فشار داد.حالا تعدادی از لامپها روشناند. حاصلجمع شمارهٔ لامپهای روشن را بهدست آورید.
- مجید، سعید، و وحید هر کدام \(k\) مهره دارند که \(k\) عددی اول است. هر کدام از آنها بهاندازهٔ یک عدد اولِ دلخواه از مهرههایشان جدا میکنند و بهترتیب \(6\)، \(26\)، و \(36\) مهره باقی میماند. حداقل تعداد مهرههایی که سعید جدا کرده چقدر است؟
- سه جهانگرد خسته و کوفته به یک مهمانسرا رفتند. آنها بر سر یک میز نشستند و سفارش یک بشقاب کوفته برنجی دادند. تا پیشخدمت غذا را بیاورد هر سه چرتی کوتاه زدند. بعد از مدتی یکی از جهانگردها از خواب بیدار شد و \(\frac{1}{3}\) بشقاب را خورد و دوباره به خواب رفت. سپس دومی بیدار شد و غافل از اینکه دوستش غذا را خورده است، او هم \(\frac{1}{3}\) غذای باقیمانده را خورد و خوابید. آخر سر، جهانگرد سوم بیدار شد و \(\frac{1}{3}\) غذای باقیمانده را خورد. صبح روز بعد که پیشخدمت رستوران آمد، هشت عدد کوفته در بشقاب مانده بود. پیشخدمت چندتا کوفته برایشان آورده بوده است؟
- فرض کنید \(n\) یک عدد صحیح مثبت باشد. اگر \(n\) مضرب \(7\) باشد و جذر آن عددی بین \(17\) و \(18\)، آنگاه چند مقدار ممکن برای \(n\) داریم؟
- اگر \(0<a<b<c\)، و بدانیم \(b\) به $a$ نزدیکتر از \(c\) است، برای چندتا از حالتهای زیر، مثال عددی وجود دارد؟



حالت اول) \(\sqrt{b}\) به \(\sqrt{a}\) نزدیکتر از \(\sqrt{c}\) است.
حالت دوم) \(\sqrt{b}\) به \(\sqrt{c}\) نزدیکتر از \(\sqrt{a}\) است.
حالت سوم) فاصلهٔ \(\sqrt{b}\) از \(\sqrt{a}\) و \(\sqrt{c}\) برابر است.
تمرینهای روزانه
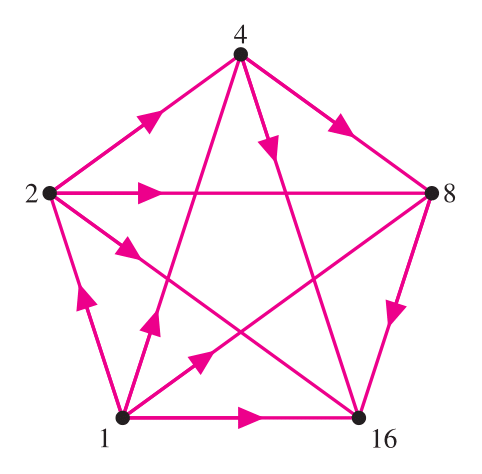
- میتوان با قرار دادن \(15\) عدد طبیعی متفاوت بر تمام رأسهای شکل زیر، آن را به نموداری تبدیل کرد که اگر از \(a\) به \(b\) یک پیکان باشد، آنگاه \(a\) شمارندهای از \(b\) باشند و برعکس، اگر \(a\) شمارندهای از \(b\) باشد یک پیکان از \(a\) به \(b\) باشد. حاصلضرب این پانزده عدد دستکم چند شمارندهٔ اول دارد؟
- چندتا از اعداد فرد مرکب بین \(50\) تا \(100\) را نمیتوان بهصورت حاصلضرب تعدادی عدد اول متمایز نوشت؟
- چند مقدار مختلف برای \(a+b\) وجود دارد اگر بدانیم \((a,b)=10\) و \([a,b]=10^{1397}\)؟
- چند عدد دو رقمی وجود دارد که تعداد شمارندههای اول آن سهتا باشد؟
- برای چندتا از موارد زیر، مثال عددی وجود دارد؟

مورد اول) عدد مثبت \(x\) که \(x^2<\sqrt{x}\)
مورد دوم) عدد مثبت $x$ که \(x<\sqrt{x}<2x\)
مورد سوم) عدد مثبت $x$ که \(\frac{1}{2}x<\sqrt{x}<x\)


ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️این سوال 5 هستش من نتونستم سوال 4 رو حل کنم ولی فکر میکنم و جوابش رو سعی میکنم بزارم ولی سوال 5 از این قراره ولی من برای همش مثال نقض آوردم که بگم نادرسته که در تصویر میبینید 🙂
اینم سوال 3
فقط به یه قانون رفتم که معلممون درس داده بود 🙂
سلام اینم سوال دوم که از روش آزمایش رفتم و دونه دونه چک کردم 🙂
البته اگه عدد گنده بود واقعا نمیشد 🙁
در ضمن سایت تکمیلی برای 2 روز فکر کنم خراب شده بود و البته حساب های کاربری پریده و دیگه نمیتونم وارد حساب کاربریم شم و البته محصول هایی که خریدم :(((((
این سوال 1 هستش
حالا دلیلش هم نوشتم ولی باز هم میگم به نظر من باید اعدادی که روی پیکان بهم وصل هستند باید تجزیه شدنشون با اعداد اول غیر تکراری باشند یعنی به غیر از اعدادی که به آن ها وصل هستند شمارنده اشون (شمارنده دومشون)عددی اول باشه که به عدد دیگه بخش پذیر نباشه 🙂
امیدوارم که تونسته باشم منظورم رو خوب رسونده باشم.