هریک از حروف داخل جدول زیر، بهجای یکی از اعداد \(1\) تا \(9\) نشستهاند.
 میدانیم:
میدانیم:
$\bullet$ اگر یک واحد از عدد سهرقمی سطر اول (یعنی $\overline{abc}$) کم کنیم، حاصل بر \(8\) و \(17\) بخشپذیر است.
$\bullet$ عدد سهرقمی سطر دوم (یعنی $\overline{def}$) مضرب \(7\) و \(13\) است.
$\bullet$ عدد سهرقمی ستون دوم (یعنی $\overline{beh}$) بر \(293\) بخشپذیر است.
$\bullet$ عدد سهرقمی ستون سوم (یعنی $\overline{cfi}$) مضرب \(109\) است.
تعیین کنید هریک از \(9\) حرف داخل جدول، بهجای چه عددی نشستهاند؟
راهنمای حل
ابتدا، با توجه به اطلاعات داده شده برای سطرهای اول و دوم، و ستونهای دوم و سوم، همهٔ حالتهای ممکن برای این سطرها و ستونها را مشخص میکنیم.
\(\bullet\) عدد سطر اول، ممکن است یکی از اعداد \(137\)، \(273\)، \(681\)، \(817\)، یا \(953\) باشد. (چرا؟)
در سطر اول، عددی سهرقمی وجود دارد که اگر یک واحد از آن کم کنیم، عددی بهدست میآید که بر \(8\) و \(17\) بخشپذیر است. نخستین عدد بخشپذیر بر \(8\) و \(17\) از حاصلضرب این دو عدد یعنی \(136\) بهدست میآید. بقیهٔ عددهای سهرقمی بخشپذیر بر \(8\) و \(17\) مضارب سهرقمی \(136\) هستند:
\[136,272,408,544,680,816,952.\]
عدد سطر اول، یک واحد بیشتر از یکی از این عددهاست، یعنی عدد سطر اول ممکن است یکی از عددهای
\[137,273,409,545,681,817,953\]
باشد؛ ولی باید از عددهای \(409\) و \(545\) صرفنظر کرد، زیرا \(409\) رقمی برابر صفر دارد و در \(545\) رقمهای برابر دیده میشود. پس عدد سطر اول، ممکن است یکی از این پنج باشد:
\[137,273,681,817,953.\]
\(\bullet\) عدد سطر دوم، ممکن است یکی اعداد \(182\)، \(273\)، \(364\)، \(546\)، \(637\)، \(728\)، یا \(819\) باشد. (چرا؟)
عدد سطر دوم بر \(7\) و \(13\) بخشپذیر است؛ یعنی عدد سطر دوم بر \(7\times13=91\) بخشپذیر است. اعداد سهرقمی زیر، بر \(91\) بخشپذیرند:
\[182,273,364,455,546,637,728,819,910.\]
توجه کنید که از عدد \(455\) که رقم تکراری دارد و همچنین عدد \(910\) که رقم صفر دارد، باید صرفنظر کنیم.
\(\bullet\) عدد ستون دوم، ممکن است یکی از اعداد \(293\)، \(586\)، یا \(879\) باشد. (چرا؟)
عدد ستون دوم بر \(293\) بخشپذیر است، پس برای ستون دوم با یکی از این عددها سروکار داریم:
\[293,586,879.\]
\(\bullet\) عدد ستون سوم، ممکن است یکی از اعداد \(218\)، \(327\)، \(436\)، \(654\)، \(763\)، \(872\)، یا \(981\) باشد. (چرا؟)
مضارب سهرقمی عدد \(109\) عبارتند از:
\[109,218,327,436,545,654,763,872,981.\]
توجه کنید که از عدد \(109\) که رقم صفر دارد و \(545\) که رقم تکراری دارد، باید صرفنظر کنیم.
در ادامه، از ترکیب عددهای ممکن در سطرها و ستونها استفاده میکنیم و حالتهای ناممکن را حذف میکنیم. از ستون دوم که فقط سه حالت دارد، شروع میکنیم.
\(\bullet\) عدد ستون دوم \(586\) است. (چرا؟)
عدد ستون دوم \(293\) نمیتواند باشد، زیرا در این صورت باید دهگان عدد سطر اول برابر \(2\) شود در حالی که هیچکدام از عددهای ممکن برای سطر اول، دهگانی برابر \(2\) ندارند.
عدد ستون دوم \(879\) نمیتواند باشد، زیرا در این صورت باید عدد سطر اول \(681\) باشد و در نتیجه صدگان عدد ستون سوم باید برابر \(1\) باشد؛ ولی در بین عددهای ممکن برای ستون سوم، هیچ عددی صدگانش برابر \(1\) نیست.
بنابراین، عدد ستون دوم برابر \(586\) است.

\(\bullet\) پس عدد سطر اول \(953\) است. (چرا؟)
چون عدد ستون دوم \(586\) است و در بین عددهای سطر اول، فقط \(953\) دهگانی برابر \(5\) دارد، پس عدد سطر اول \(953\) است.
\(\bullet\) و عدد سطر دوم \(182\) است. (چرا؟)
چون عدد ستون دوم \(586\) است، پس دهگان عدد سطر دوم باید برابر \(8\) باشد. بین عددهایی که ممکن است در سطر دوم قرار گیرند، تنها عدد \(182\) این ویژگی را دارد.

\(\bullet\) در نتیجه، عدد ستون سوم \(327\) است. (چرا؟)
ستون سوم، عددی است سهرقمی که صدگان و دهگان آن بهترتیب \(3\) و \(2\) هستند. با مراجعه به فهرست عددهای ممکن برای ستون سوم، عدد \(327\) را میبینیم.

یک خانهٔ جدول خالی مانده است؛ ولی باید همهٔ عددهای \(1\) تا \(9\) در جدول باشند. پس عدد خانهٔ خالی \(4\) است.
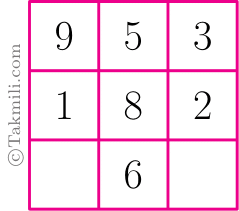
بنابراین:
\[\begin{matrix}a=9&b=5&c=3\\d=1&e=8&f=2\\g=4&h=6&i=7.\end{matrix}\]
 میدانیم:
میدانیم: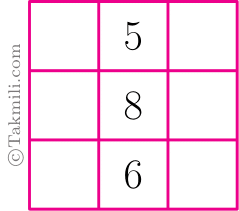



ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️