۷. ۱. ۱. ۲. به چهار روش می‌توان عدد $4$ را به‌صورت مجموع اعداد طبیعی کوچک‌تر از آن نوشت:
\[\begin{aligned}4&=1+1+1+1,\\4&=1+1+2,\\4&=1+3,\\4&=2+2.\end{aligned}\]
هریک از اعداد $3$، $5$ و $6$ را به چند روش می‌توان به‌صورت مجموع اعداد طبیعی کوچک‌تر از خودشان نوشت؟ همۀ حالت‌های ممکن را بنویسید.
راهنمای حل
با دو روش می‌توان عدد ۳ را به‌صورت مجموع اعداد طبیعی کوچک‌تر از آن نوشت. (چرا؟)
با شش روش می‌توان عدد ۵ را به‌صورت مجموع اعداد طبیعی کوچک‌تر از آن نوشت. (چرا؟)
با ده روش می‌توان عدد ۶ را به‌صورت مجموع اعداد طبیعی کوچک‌تر از آن نوشت. (چرا؟)
پرسش در کلاس ۱. به تعداد حالت‌هایی که بتوان یک عدد طبیعی را به‌صورت مجموع اعداد کوچک‌تر یا مساوی با آن عدد نوشت، تعداد اِفرازهای آن عدد می‌گویند. برای مثال، عدد ۴ را به پنج حالت می‌توان اِفراز (Partition) کرد. زیرا:
\[\begin{aligned}4&=1+1+1+1,\\4&=1+1+2,\\4&=1+3,\\4&=2+2,\\4&=4.\end{aligned}\]
در شکل زیر، اِفرازهای چه اعدادی نشان داده شده است؟
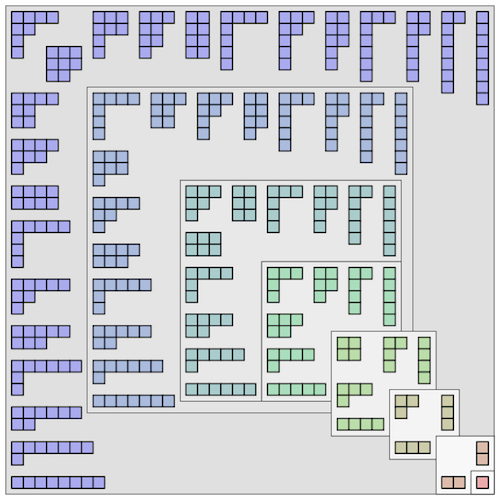
پرسش در کلاس ۲. آیا رابطه‌ای برای پیدا کردن تعداد اِفرازهای یک عدد دلخواه وجود دارد؟ دراین‌باره تحقیق کنید.
در بازی زیر، از مفهوم افراز اعداد استفاده شده است.
اگر کاربر سایت تکمیلی هستید،
وارد حساب کاربری‌تان شوید تا رکوردهای شما ثبت شود.
بله از راه …pk(N)
جواب پرسش 2 میشود بله بسط مثلث بل
عدد بل، تعداد افرازهای یک مجموعهٔ \(n\)عضوی است، نه تعداد افرازهای یک عدد طبیعی.
لطفا رابطه افراز مجموعه اعداد رو میزارید و 5 هم 7 روش و 6هم یازده روش میشود چرا شما یکی کمتر گذاشتید؟ اشتباه من کجاست؟ مرسی.
به‌صورت مسئله دقت کنید:
«هریک از اعداد $3$، $5$ و $6$ را به چند روش می‌توان به‌صورت مجموع اعداد طبیعی کوچک‌تر از خودشان نوشت؟»
نوشتهٔ بالا با تعریف افراز اعداد \(3\)، \(5\) و \(6\) کمی فرق دارد:
«به تعداد حالت‌هایی که بتوان یک عدد طبیعی را به‌صورت مجموع اعداد کوچک‌تر یا مساوی با آن عدد نوشت، تعداد اِفرازهای آن عدد می‌گویند.»
هنوز کسی فرمول مستقیمی برای شمردن تعداد افرازهای یک عدد پیدا نکرده است!
خیلی سخته
خیلی هم نه !!!