تعمیم تالس

فرض. $DE\parallel BC$.
حکم. $\frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC}$.

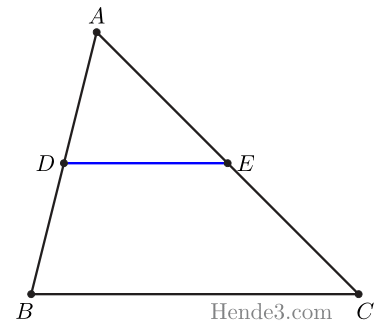
اثبات تعمیم قضیهٔ تالس.

از $E$ خطی موازی با $AB$ رسم می‌کنیم تا $BC$ را در $F$ قطع کند.

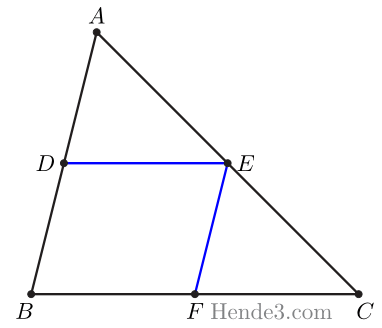
چهارضلعی $BDEF$ متوازی الاضلاع است، پس
\[BF=DE.\quad(1)\]
با استفاده از قضیهٔ تالس روابط زیر برقرار است
\[DE\parallel BC\Rightarrow \frac{AD}{AB}=\frac{AE}{AC}.\quad(2)\]
\[EF\parallel AB\Rightarrow \frac{AE}{AC}=\frac{BF}{BC}.\quad(3)\]
از رابطه‌های \((1)\)، \((2)\)، و \((3)\) نتیجه می‌شود:
$$\frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC}.$$