برای اینکه درسنامه دنباله را بهخوبی بیاموزید، حتماً روی لینک زیر کلیک کنید و از روش ارائه شده در آن استفاده کنید.
چگونه درسنامههای سایت تکمیلی را بخوانیم؟
دنباله و جملهٔ عمومی
اعداد یک دنباله معمولاً بهصورت
\[a_1,a_2,a_3,\dots\]
نوشته میشوند که در اینجا منظور از سهنقطه این است که لیست اعداد تا ابد ادامه خواهد داشت. دنبالهٔ زیر، یک مثال ساده است.
\[\begin{aligned}\begin{matrix}5,&10,&15,&20,&25,\dots\\{\color{blue}\uparrow}&{\color{blue}\uparrow}&{\color{blue}\uparrow}&{\color{blue}\uparrow}&{\color{blue}\uparrow\;\;\;\;\;}\\{\color{blue}a_1}&{\color{blue}a_2}&{\color{blue}a_3}&{\color{blue}a_4}&{\color{blue}a_5\dots}\end{matrix}\end{aligned}\]
فرمول زیر، جملهٔ عمومی دنبالهٔ بالا است.
\[a_n=5n.\]
البته میتوان فرمولهای دیگری نیز برای دنبالهٔ بالا ساخت. برای مثال، میتوان گفت که اولین جمله برابر $5$ است و برای اعداد دیگرِ آن، هر عدد از عدد قبلیاش، $5$ واحد بیشتر است؛ یا به زبان نمادین:
\[\left\{\begin{aligned}&a_1=5,\\&a_n=a_{n-1}+5,\quad n\geq2.\end{aligned}\right.\]
بهعنوان یک مثال سادهٔ دیگر، برای دنبالهٔ با جملهٔ عمومی $a_n=2n$ داریم:
\[\begin{matrix}2,&4,&6,&\dots,&2n,\dots\\{\color{blue}\uparrow}&{\color{blue}\uparrow}&{\color{blue}\uparrow}&&{\color{blue}\uparrow}\;\;\;\;\;\\{\color{blue}\text{جملهٔ اول}}&{\color{blue}\text{جملهٔ دوم}}&{\color{blue}\text{جملهٔ سوم}}&&{\color{blue}\text{اُم}n\;\text{جملهٔ}}\;\;\end{matrix}\]
توجه کنید که وقتی فرمول $a_n=2n$ را داریم، یعنی همهٔ جملههای دنباله را داریم! برای مثال، بهازای مقدارهای $1$، $2$، و $3$ برای $n$ داریم:
\[\begin{aligned}&a_{\color{red}1}=2\times{\color{red}1}=2,\\&a_{\color{red}2}=2\times{\color{red}2}=4,\\&a_{\color{red}3}=2\times{\color{red}3}=6,\\&\end{aligned}\]برای پیدا کردن جملهٔ $103$اُم، کافی است قرار دهیم $n=103$ و
\[a_{\color{red}103}=2\times{\color{red}103}=206.\]

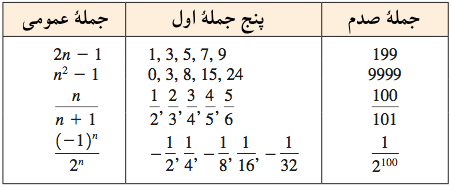
مثال ۱. برای هریک از دنبالههای زیر، پنج جملهٔ اول و جملهٔ صدم را بیابید.
الف) $a_n=2n-1$
ب) $c_n=n^2-1$
ج) $t_n=\frac{n}{n+1}$
د) $r_n=\frac{(-1)^n}{2^n}$
مثال ۲. هلن، از وقتی مشغول به کار شده است، هر ماه $100$ دلار در حساب بانکیاش پسانداز میکند. بانک، سالانه $6$ درصد سودِ ماهشمار به او میدهد. مقدار پول هلن، در ماه $n$اُم از رابطهٔ زیر بهدست میآید.
\[c_n=100\left(\frac{1.005^n-1}{0.005}-n\right).\]

الف) شش جملهٔ اول دنبالهٔ بالا را محاسبه کنید.
ب) سود پول هلن پس از $5$ سال چقدر است؟
مثال ۳. در هریک از موارد زیر، جملهٔ عمومی را پیدا کنید.
الف)
\[\frac{1}{2},\frac{3}{4},\frac{5}{6},\frac{7}{8},\dots\]
ب)
\[-2,4,-8,16,-32,\dots\]
مثال ۴. جملهٔ عمومی یک دنباله بهصورت \(t_n=\frac{2n}{n+1}\) است. جملهٔ چندم این دنباله برابر \(\frac{15}{8}\) است؟
مثال ۵. در هریک از الگوهای چوبکبریتی زیر، تعداد چوبکبریتها یک دنباله میسازند. جملۀ عمومی هر دنباله را بیابید.
الف)
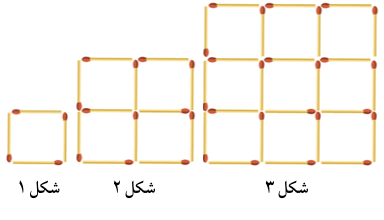
ب)
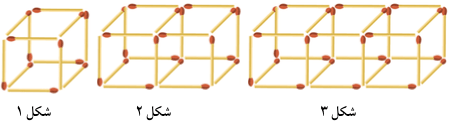
چند دنباله عجیب!
برای اینکه ذهنتان فقط به دنبالههایی که قانونهای سادهای دارند عادت نکند، سعی کنید قانون هریک از دنبالههای زیر را حدس بزنید.
\[\begin{aligned}\bullet\;&1,4,8,48,88,488,\dots\\[7pt]\bullet\;&61,21,82,43,3,\dots\\[7pt]\bullet\;&0,0,0,0,4,9,5,1,1,0,55,\dots\\[7pt]\bullet\;&2,4,6,30,32,34,36,40,42,44,46,50,\\&52,54,56,60,62,64,66,2000,\dots\\[7pt]\bullet\;&13,17,31,37,71,\dots.\end{aligned}\]
نیل اسلون (Neil Sloane)، یکی از ریاضیدانان معروف معاصر است. او یک دایرةالمعارف آنلاین به آدرس oeis.org ساخته است که در آن اطلاعات جامع و جالبی دربارهٔ هریک از دنبالههای عددی معروف وجود دارد. در ویدئوی زیر، نیل اسلون قانون هریک از دنبالههای بالا را شرح میدهد.
تمرینهای بیشتر
برای تسلط بیشتر به این درسنامه و مشاهدهٔ چند تمرین عجیب که احتمالاً آنها را ندیدهاید، حتماً تمرینهای این جلسه را حل کنید.




ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️سلام وقت بهخیر
آيا میتوان برای این «دنبالههای عجیب»، جملهی عمومی ارائه داد؟ برای هر دنبالهای با هر نوع قانونی (یا بینظمیای!) چهطور؟
سلام
دلیلی که این دنبالهها را در اینجا آوردهایم این است که ذهن خواننده شرطی نشود. کتابهای درسی این ذهنیت را در دانشآموزان میسازند که همهٔ دنبالهها جملهٔ عمومی دارند. ولی اگر با دنبالههای متنوع آشنا شوید میبینید که برای تعداد بسیار کمی از دنبالهها میتوان جملهٔ عمومی ساخت.
سلام وقت بهخیر
من مثال ۲ را متاسفانه بهکل متوجه نشدم. اگر امکانش هست دربارهی خود ساختار دنباله و اینکه دقیقاً چه چیزی داره محاسبه میشه توضیح بدید.
با تشکر
سلام
صورت مسئله که واضح است. فرمول محاسبهٔ سود، با توجه به اینکه هلن هر ماه ۱۰۰ دلار در حسابش پسانداز میکند، داده شده است. با جایگذاری اعداد میتوان مقدار سود را محاسبه کرد.
منظور شما این است که «سؤال ۲» (را که با رنگ آبی نوشته شده) متوجه نشدهاید؟
سلام
حقیقتاً منظور از «سود ماهشمار» را متوجه نشدم؛ یا حداقل ایدهی من از آن با نوعی که شما آن را در دنباله استفاده کردهاید، فرق دارد و ساختار این دنباله (که همان «سوال ۲» هست!) برایم گنگ است و نمیدانم جملهی عمومی آن باید چنین باشد
سلام
یعنی سؤال شما این است که چرا سود ۶درصد با این فرمول محاسبه میشود؟
سلام میشه توی حل این عبارت کمکم کنین ممنونم =۵۰۵۰+…+۱۰+۶+۳
سلام
سؤال مشابه سؤال شما در فصل ۱ کتاب ریاضیات تکمیلی هشتم هست.
سلام
در جواب سوال ۳ اشتباه گفتید صورتش زوج و مخرجش فرد است که درستش عکس این است.
سلام
ممنون که تذکر دادید.
اصلاح شدند.
سلام لطفا بررسی کنید مثال ها خیلی به هم میریزن کلا هرجا ریاضی نوشته قاطی پاتی شدن جمله عمومی بعضی مثال ها اصلن اونیو نشون نمیده که جواب گفتین خیلی ممنون
سلام
مثالها را نگاه کردم. هیچگونه بههمریختگی مشاهده نشد!
لطفاً بفرمایید از چه مرورگری استفاده میکنید تا دقیقتر بررسی کنیم.
با مرورگر کروم نیز آزمایش کنید و نتیجه را اطلاع دهید.
البته اگر تصمیم بر گذاشتن همچین محتوایی بود لطفا طوری باشد که کسانی که به پایه ی بالاتر از دهم می روند مانند من نیز بتوانند استفاده کند.
سلام. راستش این یک پیشنهاد هست درسته که این سایت برای ریاضیات دوره اول متوسطه هست اما اگر بشود فعالیتتان برای دوره دوم نیز باشد ممنون میشوم من پایه دهم هستم و الان کتاب تکمیلی وجود ندارد و به نظرم واقعا لازم هست که برای متوسطه دوم هم این کتب و همچین محتوایی ایجاد گردد و همچنین معرفی چنین سایت هایی که یک مورد در مبحث دنباله ها آمده بود هم بسیار مفید است و یا هر چندوقت یک بار مسائلی برای محتوای تکمیلی گذاشته شود .
باتشکر
سلام.
این سایت فقط برای ریاضیات دوره اول متوسطه نخواهد بود. در این سایت، بهمرور مطالب ریاضیات درسی و غیردرسی بارگذاری خواهد شد.
براساس نیازی که در نقاط مختلف ایران احساس میشد، اولین پروژهٔ اصلی سایت را به حل مسائل کتابهای ریاضیات تکمیلی اختصاص داده بودیم، که خدا را شکر، این پروژه تقریباً تمام شده است.
امیدواریم با همراهی شما عزیزان، بتوانیم کلیهٔ مباحث ریاضیات دبیرستانی را پوشش دهیم.