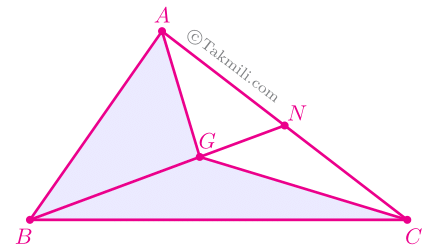
قضیه همرسی میانه ها. در هر مثلث، هر سه میانه همرسند.
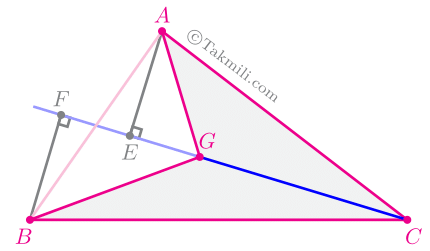
اثبات. فرض کنید در مثلث \(ABC\)، دو میانهٔ \(AM\) و \(BN\) یکدیگر را در نقطهٔ \(G\) قطع کرده باشند. پارهخط \(CG\) را رسم میکنیم و آن را از طرف \(G\) امتداد میدهیم تا ضلع \(AB\) را در نقطهٔ \(K\) قطع کند. اگر نشان دهیم که \(K\) وسط \(AB\) است، آنوقت ثابت کردهایم که سه میانهٔ \(AM\)، \(BN\)، و \(CK\) در نقطهٔ \(G\) همرسند.

با استفاده از قضیهٔ میانه-مساحت، میتوان ثابت کرد: \[S_{ABG}=S_{ACG}.\quad(1)\] (چگونه؟)
با استفاده از قضیهٔ میانه-مساحت، میتوان ثابت کرد: \[S_{ABG}=S_{BCG}.\quad(2)\] (چگونه؟)
از رابطههای \((1)\) و \((2)\) نتیجه میشود: \[S_{ACG}=S_{BCG}.\quad(3)\]
حال، از نقطهٔ \(A\) و \(B\) عمودهایی بر \(CK\) رسم میکنیم و پای این عمودها را بهترتیب \(E\) و \(F\) مینامیم.
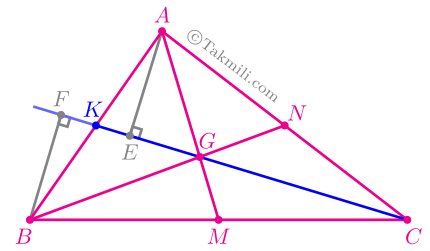
از رابطهٔ \((3)\) نتیجه میشود: \[AE=BF.\quad(4)\] (چرا؟)
از رابطهٔ \((4)\) نتیجه میشود که دو مثلث \(AGK\) و \(BGK\) هممساحت هستند. (چرا؟)
چون \(GK\) مثلث \(ABG\) را به دو مثلث هممساحت تقسیم کرده است، پس بنابه عکس قضیهٔ میانه-مساحت، داریم: \[AK=BK.\] یعنی \(CK\) میانهٔ وارد بر ضلع \(AB\) است. و در نتیجه، قضیه همرسی میانه ها ثابت شد.
پرسش. در شکل بالا، \(AE\) داخل مثلث و \(BF\) خارج مثلث است. از ارتفاعهای \(AE\) و \(BF\)، همواره یکی باید داخل مثلث باشد و دیگر خارج از مثلث. چرا؟
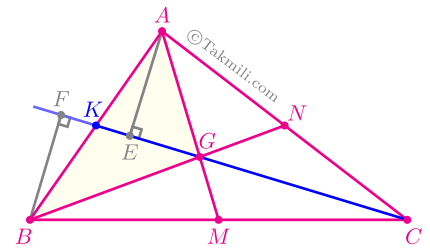
نتیجهٔ قضیهٔ همرسی میانهها. از برخورد میانههای مثلث، شش مثلث هممساحت ایجاد میشود.
اثبات. در شکل زیر، \(S_{BGM}=S_{CGM}\) ،\(S_{CGN}=S_{AGN}\)، و \(S_{AGK}=S_{BGK}\).
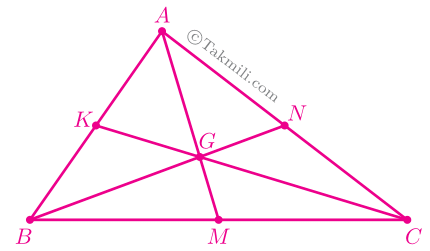
(چرا؟)
برای سادگی، قرار میدهیم:
\[\begin{aligned}S_{BGM}&=S_{CGM}=S_1\\S_{CGN}&=S_{AGN}=S_2\\S_{AGK}&=S_{BGK}=S_3.\end{aligned}\]
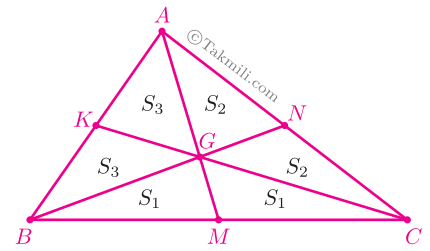
همانطور که در رابطهٔ \((1)\) دیدید (در اثبات قضیهٔ همرسی میانهها)، \(S_{ABG}=S_{ACG}\). بنابراین:
\[\begin{aligned}&S_{ABG}=S_{ACG}\\&\Rightarrow S_3+S_3=S_2+S_2\\&\Rightarrow S_3=S_2.\quad{\rm (I)}\end{aligned}\]
همچنین، با استفاده از رابطهٔ \((2)\) داریم:
\[\begin{aligned}&S_{ABG}=S_{BCG}\\&\Rightarrow S_3+S_3=S_1+S_1\\&\Rightarrow S_3=S_1.\quad{\rm (II)}\end{aligned}\]
حال از رابطههای \({\rm (I)}\) و \({\rm (II)}\) نتیجه میشود:
\[S_1=S_2=S_3.\]


ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️اگر A=(۶و۰)وB=(8-و8) نقاط روسر وتر(آن وتر قطع دایره نیاشد)باشند آنگاه مختصات مرکز و طول شعاع دایره را بدست آورید
ببخشید دبیرمون گفته مثلثی با راس های A=(۱و۲)وB=(۲و۵)وC=(۴و۱)مفروض است
مختصات نقطه همرسی میانه ها را حساب کنید با اثبات فرمول(اثبات فرمولی که xنقطه همسری میشه میانگین xنقطه ها وهمینطورy
نقطهٔ همسری یعنی چه؟
همرسی
سلام، ممنون از تدوین اثبات این قضیه ی مهم. ببخشید یه جا گفتید بنا به قضیه میانه-مساحت، مساحت مثلث ABG با مساحت مثلث BCG هست، توی بخش اول دلایل، گفتید میانه AN، ولی باید اصلاح داده بشه به میانه BN.
سلام
اصلاح شد.
با سپاس فراوان از همراهی شما
سلام، خسته نباشید، دبیرمون یه قضیه ای رو خواسته اثبات کنیم، میگم شما بلدید؟
در هر مثلث ثابت کنید فاصله میانه نظیر یک ضلع از دو راس نظیر آن ضلع به یک فاصله است.
سلام
آنچه میخواهید یکی از تمرینهای کتاب ریاضیات تکمیلی نهم است؛ تمرین ۷ صفحهٔ ۵۵ را ببینید.
سلام ببخشید توی اون *پرسش آبی* در هر حالت یک زاویه کمتر از 90 و یکی بیشتر هست بدیهی هم هست چون در غیر این صورت برابرن و مثلث متساوی الساقین هست
اما چرا شما نوشتید همیشه ؟؟؟؟ در مثلث متساوی الساقین که اینطور نیست
@ادمین عزیز میشه بررسی کنید و جواب بدید
خیلی ممنون از سایت خوبتون، من جواب سوالم را کاملا فهمیدم، خیلی ممنون
سلام این جمله که میانه ها در هر مثلثی یکدیگر را در نقطه ای درون مثلث ( نه روی محیط یا خارج از آن ) قطع می کنند درسته دیگه ؟؟
سلام
آیا برای مثلث قائمالزاویهٔ متساویالساقین هم درست است؟
بله قاعدتا من امتحان کردم داخل مثلث برخورد کرد
در جیوجبرا هم امتحان کردم همینطور شد @ادمین عزیز
میشه چک کنید خواهشا
خودتان هم امتحان کردید. درسته
سلام میشه خواهشا برای پرسش ابی رنگ کمک کنید ؟ سوال جالبیه و پاسخش شاید کمک کنه به فهم بهتر اثبات
سلام، طبق عکس آپلود شده
در پرسش قبلي با پوزش اشتباهي رخ داده لطفاً به صورت زير اصلاح نمائيد:
ثابت کنيد مراکز تلاقي ميانه ها، عمود منصف ها، و ارتفاعات هر مثلث بر يک خط راست قرار دارند
قضیه اویلر هست فکر کنم پیچیده ست
ثابت کنيد مراکز تلاقي ميانه ها، عمود منصف ها، و نيمسازهاي يک مثلث روي يک پاره خط قرار دارند
سلام
ثابت کنید سه میانه هر مثلث در نقطه ای درون آن مثلث همسر اند به طوری که فاصله این نقطه تا وسط هر ضلع یک سوم اندازه میانه و فاصله تا هر راس نظیر دو سوم اندازه میانه است؟
سلام
متوجه پرسش شما نشدم!
آیا اثبات قضیهٔ نسبت در میانههای مثلث را میخواهید؟
سلام
ایا مرکز همرسی میانه های مثلث از ضلع های مثلث به یک فاصله اند؟
سلام
خیر! محل برخورد نیمسازهای یک مثلث از ضلعهای آن به یک اندازه فاصله دارند.