قضیهٔ مثلث متساوی الساقین. در هر مثلث متساویالساقین زاویه‌های پای ساق باهم برابرند.
عکس قضیهٔ مثلث متساوی الساقین. اگر مثلثی دو زاویهٔ برابر داشته باشد، آن مثلث متساویالساقین است.
فرض. یک مثلث، مانند \(ABC\) به رأس \(A\)، متساویالساقین است.
حکم. زاویه‌های \(ABC\) و \(ACB\) برابرند.
در عکس قضیه، جای فرض و حکم عوض می‌شود.
اثبات قضیهٔ مثلث متساویالساقین. فرض کنیم مثلث \(ABC\) به‌رأس \(A\) متساویالساقین باشد. می‌خواهیم ثابت کنیم که \(\widehat{B}=\widehat{C}\).
نیمساز زاویهٔ \(A\) را رسم می‌کنیم و محل برخورد آن با \(BC\) را \(D\) می‌نامیم.
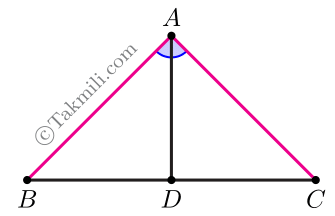دو مثلث \(ABD\) و \(ACD\) در حالت ضزض همنهشت هستند. (چرا؟)
از همنهشتی دو مثلث \(ABD\) و \(ACD\) نتیجه می‌شود که \(\widehat{B}=\widehat{C}\).
اثبات عکس قضیهٔ مثلث متساویالساقین. فرض کنیم در مثلث \(ABC\) اندازهٔ دو زاویهٔ \(B\) و \(C\) برابر باشد. می‌خواهیم ثابت کنیم که \(AB=AC\).
نیمساز زاویهٔ \(A\) را رسم می‌کنیم و محل برخورد آن با \(BC\) را \(D\) می‌نامیم.
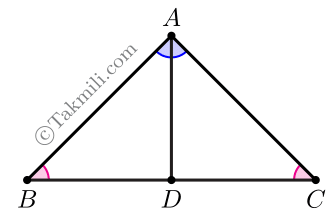
دو مثلث \(ABD\) و \(ACD\) در حالت ززض همنهشت هستند. (چرا؟)
از همنهشتی دو مثلث \(ABD\) و \(ACD\) نتیجه می‌شود که \(AB=AC\).
سلام وقت بخیر مگر ما نمی گفتم یکی از حالت های هم نهشتی دو زاویه و ضلع بین است ولی در این اثبات ضلع مساوی دو مثلث بین دو زاویه های مساوی نیست ؟
سلام
یکی دیگر از حالت‌های همنهشتی ززض است. حتماً قضیهٔ ززض و اثبات آن را بخوانید، و تمرین‌های مربوطه را از کتاب ریاضیات تکمیلی هشتم و نهم حل کنید.
سلام خسته نباصید دایره ای به مرکز p و دایره ای به مرکز Qرا در دو نقطه XوYقطع کرده اند.خب بنابراین آیا می توان گفت که XYعمودمنصف PQاست؟خب این که جوابش خیره گفته یه شرطی اضافه کنید که XY عمود منصف PQباشد.اون شرط چیه و چرا
سلام
باید دایره‌ها هم‌اندازه باشند.
سلام
اثبات کنید در مثلث ABC اگر نیمساز B و C برابر باشد حتما مثلث ، مثلث متساوی الساقین است یعنی AB = AC
سلام
این یک مسئلهٔ بسیار معروف است که اثبات آن کمی پیچیده است.
کتاب بازآموزی و بازشناخت هندسه را دانلود کنید و صفحات ۲۹ و ۳۰ را بخوانید.
سلام.
ارتفاع مثلث متساوی الساقین رسم شده است . حالت هم نهشتی دو مثلث را بنویسید .
از کجا بفهمیم ارتفاع مثلث نیمساز زاویه است یا عمود منصف قاعده ؟
سلام
وقتی همنهشتی دو مثلث را ثابت کنید، آنچه گفته‌اید اثبات می‌شود.
سلام ببینید ما میتونیم با همین روش رسم نیمساز یا میانه و اثبات همنهشتی می توان فهمید زاویه های پای ساق برابر است پس با استفاده از این دانش و عمود بودن ارتفاع می توان با ض ز ض (دو ضلع ساق و یکی مشترک و زاویه بین ) یا ز ض ز (دو زاویه روی ساق یا عمود و ارتفاع یا ضلع)
سلام ایا میتونیم در مثلت قایم زاویه برای اثبات همنهشتی از زاویه ی 90 درجه استفاده کنیم؟
سلام
بله. می‌توانید از برابری زاویه‌های ۹۰ درجه در دو مثلث قائم‌الزاویه استفاده کنید.
سلام
برای اثبات عکس قضیه آیا می توان از قضیه ارتفاع بودن نیم ساز در مثلث متساوی الساقین استفاده کنیم؟(که نتیجه بگیریم زوایای ADC و ADB برابرند و به حالت ززض ولی بدون استفاده از برابری A1 و A2 برویم.)
از این اثبات برابری دو زاویه ADB و ADC(عمود بودن نیم ساز بر قاعده در مثلث متساوی الساقین) نتیجه می شود،به خاطر همین شک دارم.(فکر کنم نمی توان برای اثبات یک قضیه از چیزی استفاده کرد که از آن قضیه نتیجه شود( اسم علمی دارد؟) شک من برای این است که این قضیه برابری دو زاویه ADC و ADB از جای دیگر کاملا مستقل از قضیه مثلث متساوی الساقین اثبات می شود یا نه( تا بفهمیم می توان از قضیه ارتفاع بودن نیم ساز در مثلث متساوی الساقین استفاده کرد یا نه)).
و از جایی دیگر برابری این دو زاویه(عمود بودن نیم ساز بر قاعده در مثلث متساوی الساقین) از قضیه وتر و یک ضلع( یکی از حالات هم نهشتی مثلث قائم الزاویه) هم حاصل می شود.(در عکس قضیه عمود منصف که هم نهشتی دو مثلث از قضیه وتر و یک ضلع اثبات می شود.) ولی در قضیه وتر و یک ضلع هم از حالت هم نهشتی ض ض ض استفاده شده است.(نمی دانم این ربطی داشت یا نداشت! در قضیه وتر و یک ضلع آیا از حالت هم نهشتی ززض استفاده می شود؟ یا اصلا مهم نیست که از کدام حالت هم نهشتی اثبات شود؟)
سلام
چگونه ثابت می‌کنید که در مثلث متساویالساقین، ارتفاع نیمساز است؟
از همین اثبات(عکس قضیه مثلث متساوی الساقین)
اثبات می کنیم دو زاویه ADB و ADC برابرند( چون دو مثلث هم نهشت هستند )
اینگونه می توان استفاده کرد؟(فکر کنم نمی شود چون نمی توان از چیزی برای اثبات یک مسئله کمک گرفت(استفاده کرد) که از اثبات آن نتیجه می شود.)
ولی ممکن است عمود بودن نیم ساز بر قاعده مثلث در مثلث متساوی الساقین از جایی دیگر که مستقل از این اثبات بالا هست نتیجه شود و بتوان برای اثبات بالا استفاده کرد.
همان‌طور که گفتید، نمیشود.
حتی شما هنوز ثابت نکرده‌اید که عمود داخل مثلث می‌افتد یا بیرون آن!
اونجا یه اشتباه کردید مثلث به حالت زضز همنهشن میشه نه ززض
دقت کنید که ضلع \(AD\) بین زاویه‌های رنگ شده نیست!
میشه بدون قضیه ززض بگیم فقط با هم نهشتی بگیم ؟
منظورتان از «فقط با همنهشتی» چیست؟ برای اثبات اینکه دو مثلث همنهشت‌اند یا باید ثابت کنید که هر جزء مثلث اول (یعنی ضلع‌ها و زاویه‌ها) با اجزاء متناظرش در مثلث دوم برابر است یا از قضیه‌های همنهشتی استفاده کنید.
آیا در کل میتونیم برای اثبات در مثلث متساوی الساقین از برابری زاویای پای ساق استفاده کنیم؟
اگر گفته باشندdوسط ضلع b c است آن موقع به حالت ض ض ض میشد؟
یعنی می‌خواهید صورت قضیه را عوض کنید؟
سلام وقت بخیر ببخشید من یک سوال داشتم میشه بگین ایا دومثلث ABD و ACD از حالت وز همنهشت هستند یا نه به نظر من هستن چون نیمساز متساوی الساقین مانند ارتفاع هست و اگه از این حالت همنهشت هستن لطفا دلیل تونم بگین.ممنون
سلام
در هر دو حالت بالا، نیمساز رسم شده است، نه ارتفاع! پس نمی‌توان از قائم‌الزاویه بودن مثلث‌های \(ABD\) و \(ACD\) استفاده کرد.
توجه کنید که اگر در این قضیه‌ها بخواهید ارتفاع را بکشید، حتماً باید ثابت کنید که ارتفاع رسم شده، داخل مثلث می‌افتد.
سلام
اگر کسی بخواهد با ارتفاع این موضوع رو اثبات کند چطوری باید اثبات کند ارتفاع ها درون مثلث هستن ؟ ایا امکان پذیر است ؟
سلام
امکان‌پذیر هست.
سلام میشه روشش رو بگید ؟ همیشه توی اثبات هایی که با ارتفاع سر و کار داریم درباره همین موضوع که از کجا فهمیدن ارتفاع داخل میفته مشکل پیدا میکنم…
سلام
از برهان خلف استفاده کنید. (فرض کنید که ارتفاع بیرون از مثلث باشد و …)
میشه یکم دیگه هم درباره اش توضیح بدید ؟ یعنی بیایم بگیم که نمیشه چون مجموع زوایا از 180 بیشتر میشه ( چون اون وقت دو تا زاویه باز میشه ) یا منظور دیگه ای دارید ؟
برهان خلف جزء مباحث دورهٔ دوم دبیرستان است.
سلام
قضیه مثلث متساوی الساقین با ض ز ض اثبات نمیشه. بلکه با “و ض” هست
سلام
در اثبات بالا از حالت ضزض استفاده شده است. لطفاً بفرمایید که به کدام قسمت از اثبات مشکوک هستید؟
در بحث “ض ز ض” دو تا از زاویه ها باید متساوی الساقین باشند که در مخصوصا مثلث های قائم الزاویه که یک زاویه 90 درجه دارند، حالت “و ض” پیش می آید؛ چون دو مثلث ABD و ACD هم قائم الزاویه اند، پس حالت همنهشتی، “و ض” است
نگفتید که در راه‌حل بالا، چرا استفاده از حالت «ضزض» غلط است! لطفاً ابتدا دقیقاً مشخص کنید که ایراد استدلال بالا چیست.
سلام در قسمت اول میتوانیم میانه را رسم کنید و دو مثلث را در حالت ض ض ض هم نهشت کنیم ؟
همچنین در قسمت دو میتوایم ابتدا برای تساوی بودن D1و D2 دلیل بیاوریم و سپس دو مثلث را در حالت ز ض ز هم نهشت کنیم ؟
سلام
آنچه برای قسمت اول نوشته‌اید، درست است.
برای قسمت دوم:
وقتی ما درستی قضیهٔ ززض را (با استفاده از قضیهٔ زضز) پذیرفته‌ایم، دیگر نیازی نیست که هربار آن را به حالت زضز تبدیل کنیم. (برای مشاهدهٔ اثبات قضیهٔ ززض اینجا را کلیک کنید.)
قضیهٔ ززض، در قسمت «ب» تمرین ۱۱ صفحهٔ ۹۸ نیز آمده است.
یک نکتهٔ اساسی در قضیه‌های هندسه هست. درستی هر قضیه، با آنچه که قبلاً درستی آن را پذیرفته‌ایم ثابت می‌شود. وقتی قضیه‌ای را پذیرفتیم، میتوانیم از آن استفاده کنیم. بنابراین، نیازی نیست که در راه‌حل مسئله‌ای که داریم، درواقع، همان اثبات قضیه را بنویسیم تا به قضیهٔ قبلی برسیم! مثلاً برای اثبات قضیهٔ زضز نیز از حالت ضزض استفاده می‌شود. (برای مشاهدهٔ قضیهٔ زضز، اینجا را کلیک کنید.)
اگر در امتحان ها مثلا استانی نوبت دوم و اینا ززض رو بنویسیم درست محسوب میشه؟
بله!
در واقع، حالت ززض تفاوت زیادی با حالت زضز نداره. وقتی دو زاویه برابر باشند، بنابه قضیهٔ مجموع زاویه‌های مثلث، زاویهٔ سوم نیز برابر است.
اما، حالت ززض از این جهت مهم است که اثبات آن بدون قضیهٔ مجموع زاویه‌های مثلث (برای هندسهٔ بالاتر از سطح دبیرستان) نیز امکان‌پذیر است.
آخرش باید AC=AB می نوشتین
با سپاس فراوان از شما.
اصلاح شد.