محل برخورد دو خط $2x-y=1$ و $y+3x-4=0$، نقطهٔ $\big[{1\atop1}\big]$ است. (چرا؟)
برای بهدست آوردن نقطهٔ برخورد این دو خط، کافی است دستگاه معادلات زیر را حل کنیم.
\[\left\{\begin{aligned}y+3x-4&=0\\2x-y=1\end{aligned}\right.\]
با جمع زدن طرفین دو معادلهٔ بالا، داریم:
\[\begin{aligned}&(y+3x-4)+(2x-y)=0+1\\&\Rightarrow5x-4=1\\&\Rightarrow5x=5\\&\Rightarrow x=1.\end{aligned}\]
با جایگذاری $x=1$ در یکی از معادلههای داده شده، $y$ را بهدست میآوریم:
\[\begin{aligned}&2x-y=1\\&\Rightarrow2(1)-y=1\\&\Rightarrow y=1.\end{aligned}\]
بنابراین، دو خط $2x-y=1$ و $y+3x-4=0$، یکدیگر را در نقطهٔ $\big[{1\atop1}\big]$ است.
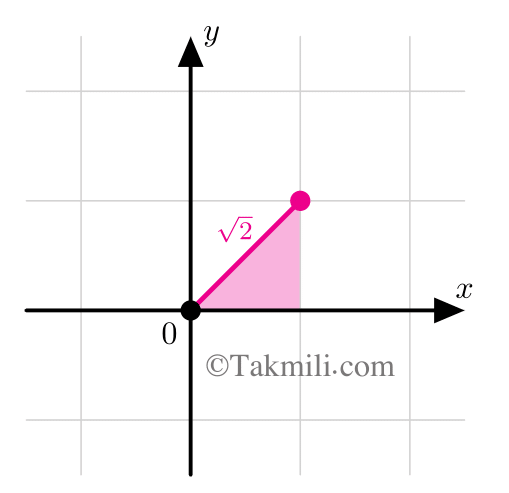
پس فاصلهٔ محل برخورد دو خط $2x-y=1$ و $y+3x-4=0$ از مبدأ مختصات، $\sqrt{2}$ است. (چرا؟)
برای پیدا کردن فاصلهٔ نقطهٔ $\big[{1\atop1}\big]$ از مبدأ مختصات، کافی است طول وتر مثلث قائمالزاویهٔ زیر را محاسبه کنیم. با استفاده از قضیهٔ فیثاغورس، طول وتر این مثلث قائمالزاویه بهدست میآید.


ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️برای پرسش آبی رنگ باید گفت که برای هر دو نقطه دلخواه در دستگاه مختصات ابتدا تغییرات ایکس ( طول) را مشخص می کنیم
(همان دلتا ایکس) که در راستای افقی است و سپس تغییرات وای ( عرض ) را مشخص می کنیم ( همان دلتا وای ) که در راستای عمودی است حال چون این دو عمود بر هم خواهند بود با توجه به رابطه فیثاغورس :
dx^2+dy^2=|distance|^2
پس فاصله می شود رادیکال (dx^2+dy^2) توجه شود که قرینه این رادیکال را در نظر نمی گیریم چون منفی است اما فاصله همواره نا منفی خواهد بود