مطابق مراحل زیر، میتوان به هر پاره‌خط یک دست‌انداز اضافه کرد:
مرحلهٔ اول. پاره‌خط را به سه قسمت مساوی تقسیم میکنیم.
مرحلهٔ دوم. یک مثلث متساوی‌الاضلاع روی پاره‌خط میانی می‌سازیم.
مرحلهٔ سوم. پاره‌خط میانی را حذف میکنیم.
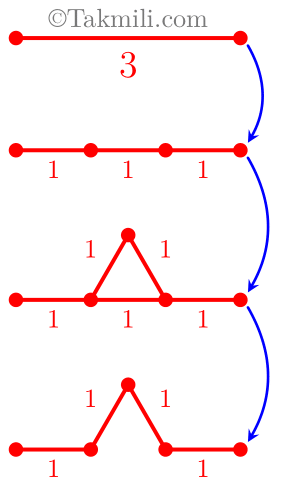
در شکل زیر، سه مرحلهٔ بالا روی پاره‌خطی به طول \(3\) اجرا شده است.
آرمیتا روی یک پاره‌خط به طول \(n\) یک دست‌انداز ایجاد کرد و مسیر ساخته شده را مسیر ۱ نامید. سپس روی هریک از پاره‌خط‌های مسیر ۱ یک دست‌انداز ایجاد کرد و مسیر ساخته شده را مسیر ۲ نامید. او همین کار را تکرار کرد تا مسیر ۳، مسیر ۴، و مسیر ۵ ساخته شوند. اگر \(n\) عددی طبیعی بوده باشد و طول مسیر ۵ نیز عددی طبیعی شود، آن‌وقت کمترین مقدار ممکن برای \(n\) چیست؟
در شکل زیر، مسیر ۱ و مسیر ۲ آرمیتا رسم شده است.
منتظر راه‌حل‌های تشریحی شما هستیم.
می‌توانید از راه‌حل خود عکس بگیرید و آن را در کامنت‌های زیر آپلود کنید.
برای آشنایی با روش آپلود عکس در سایت تکمیلی، بخش کامنت‌گذاری پرسش‌های متداول را بخوانید.
در وب‌سایت تکمیلی، هر هفته یک مسئلهٔ جدید منتشر می‌‌شود. برای مشاهدهٔ مسائل هفته‌های دیگر، روی لینک زیر کلیک کنید.
باسلام
ببینید کمترین مقدار ممکن برای n فک کنم 3 به توان 5 باشه یعنی 232 چون اگه ببینید برای ساخته شدن مسیر دوم هرکدوم از پاره خط های مسیر اول به سه قسمت تقسیم شده و روی میانی یک مثلث ایجاد شده . پس برای ساخته شدن مسیر های بیشتری که طول هر کدوم از پاره خط هاش طبیعی باشه باید هر خط مضرب 3 باشه که کوچکترین مضرب طبیعی 3 خود 3 هست و حتی با آزمون خطا هم میشه پی به درستی این برد به عنوان مثال اگه شما بخواین فقط مسیر دو را بسازید مسیر یک باید حداقل 3 به توان 2 یعنی 9 باشد اگر مسیر هم بخواین بسازین باید 3 به توان 3 یعنی 27 باشد پس برای ساختن مسیر 5 أم n باید حداقل 3 به توان 5 یعنی 243.
سلام وقت بخیر .به نظر من کمترین مقدارش ۳ به توان ۵ هست
از اونجایی که ما روی ضلع میانی مثلث متساوی الاضلاع را می سازیم میتوان پی برد که تمام پاره خط هایی که بوجود می آیند همگی با هم برابرند و طول هر ضلع مضرب سه است و از طرفی چون آرمیتا مسیر ۱ را به سه قسمت تقسیم کرده و چون طبق گفته ی سوال هم مسیر ۵ و هم n عدد طبیعی ای هستند می توان پی برد که n برابر ۳ به توان ۵ است ، همچین با ساختن مثل متساوی الاضلاع روی هر ضلع، در واقع هر ضلع را به سه قسمت تقسیم میکنیم! پس می توان گفت که n=3^5=243
سلام
از نظر کمترین مقدار ممکن برای n از نظر من 3 به توان 5 است یعنی 232چون اگه ببینید برای ساخته شدن مسیر دوم هرکدام از پاره خط های مسیر اول به سه قسمت تقسیم شده و روی میانی یک مثلث ایجاد شده. پس برای ساخته شدن مسیر های بیشتری که طول هر کدوم از پاره خط هاش طبیعی باشه باید هر خط مضرب 3 باشه که کوچکترین مضرب طبیعی 3 خود 3 هست
و حتی با ازمون خطا هم میشه پی به درستی این برد
به عنوان مثال اگه شما بخواین فقط مسیر دو را بسازید مسیر یک باید حداقل 3 به توان 2 یعنی 9 باشد
اگر مسیر 3 هم بخواین بسازین باید 3 به توان 3 یعنی 27 باشد
پس برای ساختن مسیر 5 ام n باید حداقل 3 به توان 5 یعنی 243 باشد.
با سلام
کمترین طول باید ۲۴۳ باشد . چون در هر مسیر طول پاره خط های واحد ، ۳ به توان منفی ۱ برابر طول پاره خط های مسیر قبلی می شود ؛ باید طول مسیر ۲۴۳ باشد تا در نهایت طول پاره خط های واحد در مسیر ۵ ، ۱ شود
طول پاره خط های واحد در مسیر ۸۱:۱=۳÷۲۴۳۱
طول پاره خط های واحد در مسیر ۲ :۲۷=۳÷۸۱
طول پاره خط های واحد در مسیر ۳ : ۹=۳÷۲۷
طول پاه خط های واحد در مسیر ۴ : ۳=۳÷۹
طول پاره خط های واحد در مسیر ۵ :۱= ۳÷۳
کمترین مقدار ممکن برای n ، عدد ۲۴۳ می باشد !