۶۶. در کنار جاده‌ای تیرهای سیمانی به فاصله‌های برابر وجود دارد. حامد از تیر اول آغاز به حرکت کرد و بعد از \(6\) دقیقه از کنار تیر ششم گذشت. اگر حامد با همین سرعت به حرکتش ادامه دهد، پس از چند دقیقه (از آغاز حرکت) از کنار تیر بیست‌وششم می‌گذرد؟
۱) \(26\) دقیقه
۲) بیش از \(26\) دقیقه
۳) کمتر از \(26\) دقیقه
۴) هر سه گزینهٔ بالا می‌تواند درست باشد.
۶۷. مهسا جمع اعداد زیر را تا عدد \(n\) (که خودش مقدار \(n\) را می‌داند) ادامه می‌دهد. کدام‌یک از گزینه‌ها می‌تواند حاصل عبارت زیر باشد؟
\[(-100)+(-90)+(-80)+(-70)+\dots+n=?\]
۱) \(110\)
۲) \(120\)
۳) \(130\)
۴) \(140\)
۶۸. یک کیک به شکل زیر، روی میز قرار دارد.
می‌خواهیم با یک چاقو آن را به‌صورت عمودی با تعدادی برش، تکه‌تکه کنیم. برش‌ها به این صورت انجام می‌شود که هر برش از دو نقطه می‌گذرد به‌طوری‌که بین هر دو نقطه، سه نقطهٔ دیگر قرار می‌گیرد. پس از پایان برش‌ها، این کیک به \(n\) تکه تقسیم می‌شود. باقی‌ماندهٔ تقسیم \(n\) بر \(4\) چه عددی می‌شود؟
۱) صفر
۲) یک
۳) دو
۴) سه
۶۹. حاصل‌ضرب اندازه‌های زاویه‌های یک مثلث، کمتر از \(1\) است. با‌توجه‌به ادعاهای زیر، گزینهٔ درست کدام است؟
ادعای اول: حداقل اندازهٔ یک زاویه از این مثلث بیشتر از \((90-1)\) درجه است.
ادعای دوم: اندازهٔ همهٔ زاویه‌های این مثلث کمتر از \((90-1)\) درجه است.
۱) هر دو ادعا درست هستند.
۲) فقط ادعای اول درست است.
۳) فقط ادعای دوم درست است.
۴) هر دو ادعا غلط هستند.
۷۰. در سال جاری یکی از معتبرترین جایزه‌های ریاضی جهان به مریم میرزاخانی (متولد \(1977\) میلادی یا \(1356\) شمسی) اهدا شد. روی نشانی که به او اهدا شد، تصویر ارشمیدس (\(287\)-\(212\) پیش از میلاد) حک شده است. میرزاخانی چند سال پس از سال تولد ارشمیدس به‌دنیا آمده است؟
۱) \(2264\)
۲) \(2189\)
۳) \(1765\)
۴) \(1690\)
۷۱. کدام‌یک از گزینه‌های داده شده می‌تواند صورت مسئله‌ای باشد که معادله‌اش به‌صورت \(2x+3=5x\) است؟
۱) دو بازیکن فوتبال روزی سه کیلومتر می‌دوند. پنج بازیکن فوتبال روی چند کیلومتر می‌دوند؟
۲) قیمت پنج کیلو سیب، سه‌هزار تومان بیشتر از قیمت دو کیلو از همان سیب است. قیمت سه کیلو سیب چند هزار تومان است؟
۳) سه روز بعد از دو روز دیگر، پنج‌شنبه خواهد بود. امروز چندشنبه است؟
۴) اندازهٔ زاویه‌ای که دو برابر اندازه‌اش، سه واحد بیشتر از پنج‌برابر اندازه‌اش است، چقدر است؟
۷۲. اگر مربع عددی به آن اضافه شود، عددِ حاصل \(57\) خواهد بود. چندتا از اعداد زیر می‌تواند مقدار آن عدد باشد؟
\[57,\;42,\;-8,\;8,\;-87\]
۱) \(1\)
۲) \(2\)
۳) \(3\)
۴) صفر
۷۳. پدری \(45\) سال دارد. سه فرزند او \(4\)، \(12\)، و \(15\) ساله‌اند. پس از چند سال سن پدر با مجموع سن فرزندانش برابر می‌شود؟
۱) \(7\)
۲) \(14\)
۳) \(21\)
۴) \(28\)
۷۴. هادی و هدی می‌خواستند ثابت کنند مجموع زاویه‌های مثلث \(180^\circ\) است. کدام گزینه درست است؟
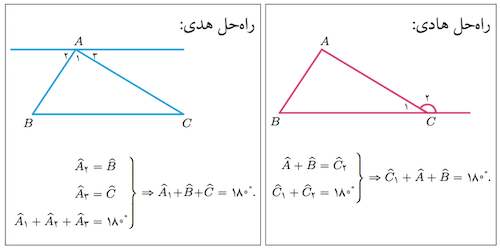
۱) راه‌حل هادی درست و راه‌حل هدی نادرست است.
۲) راه‌حل هادی نادرست و راه‌حل هدی درست است.
۳) راه‌حل هادی درست و راه‌حل هدی نادرست است.
۴) راه‌حل هادی نادرست و راه‌حل هدی نادرست است.
۷۵. بیشترین تعداد اعداد طبیعی دو رقمی پشت‌سرهم که هیچ‌کدام اول نباشند، چندتا است؟
۱) \(5\)
۲) \(6\)
۳) \(7\)
۴) \(8\)
۷۶. چند عدد طبیعی دورقمی وجود دادر که اعداد قبل و بعد از آن، یکی مربع کامل و دیگری اول باشد؟
۱) \(2\)
۲) \(3\)
۳) \(4\)
۴) \(5\)
۷۷. در تساوی زیر، \(x\) کدام است؟
\[\frac{46}{2.5}\times5=\frac{x}{0.125}.\]
۱) $5.75\times2$
۲) $11.75$
۳) $2.25^2\times2$
۴) $2.75\times4$
۷۸. در شکل زیر، اگر بدانیم \(a=90^\circ\)، \(b=68^\circ\)، و \(c=68^\circ\)، کدام دو خط موازی‌اند؟
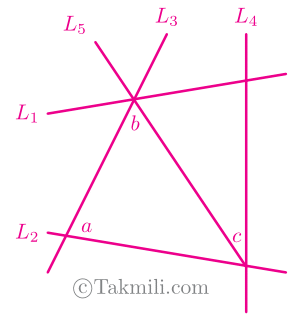
۱) $L_3$ و $L_4$
۲) $L_1$ و $L_2$
۳) $L_2$ و $L_5$
۴) اطلاعات مسئله کافی نیست.
۷۹. کدام گزینه، ساده شدهٔ عبارت \(\dfrac{a^2-b^2}{ab}-\dfrac{a^2-b^2}{ab-a^2}\) است؟ \((a,b\ne0)\)
۱) $\frac{a+b}{b}$
۲) $\frac{a^2-2b^2}{ab}$
۳) $a^2$
۴) $a-2b$
۸۰. می‌خواهیم با روش غربال، اعداد اول کوچک‌تر از \(5000\) را تعیین کنیم. کدام دیرتر حذف می‌شود؟
۱) $3256$
۲) $4141$
۳) $3553$
۴) $3801$
۸۱. در شکل زیر، \(AB\parallel CL\) و سه نقطهٔ \(B\)، \(D\)، و \(E\) روی یک خط قرار دارند. \(L\widehat{D}E\) با کدام برابر است؟
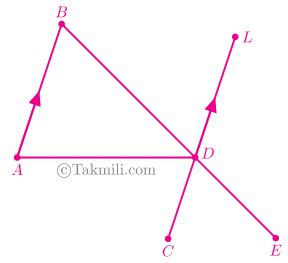
۱) $\widehat{A}+\widehat{B}$
۲) $\widehat{B}+A\widehat{D}B$
۳) $\widehat{A}+A\widehat{D}B$
۴) $C\widehat{D}A+B\widehat{D}L$
۸۲. اگر بدانیم \(A\frac{2}{3}=2+\frac{2}{3}\div\frac{1}{5}\) و بدانیم \(B=\dfrac{\frac{3}{2}-1}{\frac{4+12\div(-6)}{-4-1}}\)، آنگاه \(A-B\) کدام است؟
۱) $\frac{12}{79}$
۲) $\frac{71}{12}$
۳) $\frac{145}{12}$
۴) $\frac{-175}{12}$
۸۳. در شکل زیر، چند نقطه مانند \(D\) می‌توان یافت به‌طوری‌که \(A\)، \(B\)، \(C\)، و \(D\) رأس‌های متوازی‌الاضلاع باشد؟
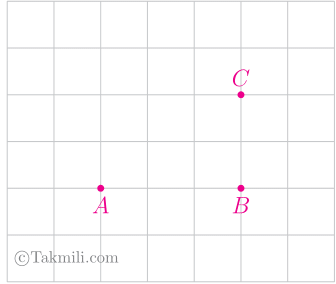
۱) هیچ
۲) \(1\)
۳) \(2\)
۴) \(3\)
۸۴. چندتا از اعداد زیر گویا است؟
\[\frac{2}{3},\;-3,\;\frac{\frac{-2}{3}}{\frac{-5}{4}},\;\frac{0}{1},\;\frac{3}{-5},\;0.1\]
۱) \(4\)
۲) \(5\)
۳) \(6\)
۴) \(7\)
۸۵. در شکل زیر، \(x\) چند درجه است؟
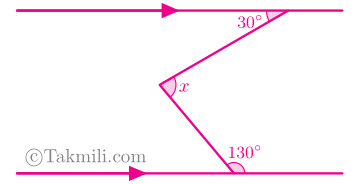
۱) \(70\)
۲) \(80\)
۳) \(90\)
۴) اطلاعات مسئله کافی نیست.
۸۶. اگر \(a > 0\)، \(b <0\)، و \(c < 0\)، آنگاه چندتا از عبارت‌های زیر منفی هستند؟
\[ab^2c,\;(a-b)^3,\;(ac-b^2c),\;\frac{a^3b^3}{b^6c^2}\]
۱) حداقل سه‌تا
۲) حداکثر سه‌تا
۳) بیشتر از سه‌تا
۴) کمتر از سه‌تا
۸۷. حاصل عبارت \((x-3)(x^2-3x+9)\) کدام است؟
۱) $x^3-6x^2+18x-27$
۲) $x^3-6x^2-18x+27$
۳) $x^3-27$
۴) $x^3+27$
۸۸. حاصل عبارت \(6\div2(1+2)\) کدام است؟
۱) \(1\)
۲) \(3\)
۳) \(6\)
۴) \(9\)
متن زیر را با دقت بخوانید…
یک چندجمله‌ای را ترید (trade) می‌نامیم هرگاه:
\(\bullet\) اولاً درجهٔ آن چندجمله‌ای نسبت به همهٔ متغیرهایش یک باشد.
\(\bullet\) ثانیاً مجموع ضرایب جملاتی که یک متغیر دلخواه در آن ظاهر می‌شود، برابر صفر باشد.
برای مثال، چهارجمله‌ای \(xy+zw-xz-yw\) یک ترید است. زیرا متغیرهای \(x\) در جمله‌های \(xy\) و \(-xy\) آمده است. این استدلال برای متغیرهای \(y\)، \(z\)، و \(w\) نیز صادق است.
با توجه به متن بالا، به سؤال‌های ۸۹ و ۹۰ پاسخ دهید.
۸۹. چندتا از عبارت‌های زیر ترید هستند؟
\[\begin{aligned}&\bullet ab-ad+bc-cd\\&\bullet ac-2ad-2bc+bd+ab+cd\\&\bullet ab+cd-ac-bd\end{aligned}\]
۱) هیچ
۲) یکی
۳) دوتا
۴) سه‌تا
۹۰. حاصل چندتا از عبارت‌های زیر، ترید است؟
\[\begin{aligned}&\bullet(a-b)(c-d)+(a-c)(b-d)\\&\bullet(a+c)(b-d)\\&\bullet(a-c)(b-d)\end{aligned}\]
۱) هیچ
۲) یکی
۳) دوتا
۴) سه‌تا
