۵۱. کدام مجموعه نشان‌دهندهٔ اعضای مجموعهٔ \(\Big\{(-1)^{\frac{n(n+1)}{2}}\times n\,\big|\,n\in\mathbb{W},n\leq5\Big\}\) است؟
۱) \(\{0,1,2,-3,-4,5\}\)
۲) \(\{0,-1,2,3,-4,-5\}\)
۳) \(\{0,1,-2,-3,4,5\}\)
۴) \(\{0,-1,-2,3,4,-5\}\)
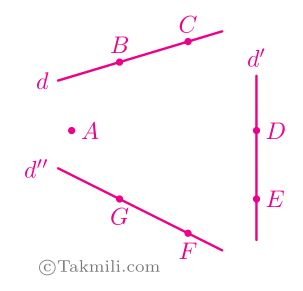
۵۲. با نقاط مشخص شده روی شکل، مثلثی به‌دلخواه رسم می‌کنیم. احتمال آنکه این دو مثلث دو شرط زیر را داشته باشد، چقدر است؟
\(\bullet\) یکی از رئوس حتماً \(A\) باشد.
\(\bullet\) دو رأس دیگر همزمان روی \(d’\) نباشند.
۱) \(\frac{3}{5}\)
۲) \(\frac{2}{5}\)
۳) \(\frac{11}{35}\)
۴) \(\frac{29}{35}\)
۵۳. مجموعهٔ \(A=\{1,2,\dots,18\}\) مفروض است. چند زیرمجموعهٔ حداکثر \(5\) عضوی از \(A\) می‌توان نوشت که شامل اعضای \(1\)، \(2\)، و \(3\) باشند؟
۱) \(120\)
۲) \(121\)
۳) \(122\)
۴) \(123\)
۵۴. در نمایش اعشاری عدد \(\frac{2039}{1650}\)، ۲۶اُمین رقم بعد از ممیز کدام است؟
۱) \(5\)
۲) \(7\)
۳) \(3\)
۴) \(2\)
۵۵. مستطیلی به ابعاد \(a\times b\) \((a > b)\) مفروض است. اگر مستطیلی متشابه با آن به ابعاد \(c\times d\) \((c > d)\) رسم کنیم و روی قطرهای هر دو مستطیل مثلث‌های متساوی‌الاضلاعی بنا کنیم، نسبت مساحت مثلث‌ها کدام است؟
۱) \((\frac{a}{d})^2\)
۲) \((\frac{c}{b})^2\)
۳) \((\frac{a}{c})^2\)
۴) \((\frac{a}{b})^2\)
۵۶. چند گزاره از گزاره‌های زیر همواره درست هستند؟
\(\bullet\) ریشهٔ سوم هر عدد از ریشهٔ دوم آن کوچکتر است.
\(\bullet\) تساوی \(\sqrt[n]{\sqrt[n+1]{a}}=\sqrt[n+1]{\sqrt[n]{a}}\) \((n\geq2,n\in\mathbb{N})\) فقط در صورتی برقرار است که \(a\geq0\).
\(\bullet\) اگر \(x < 0\)، آنگاه \(-3\sqrt[3]{x^3}-2\sqrt{x^2}=-x\).
۱) \(0\)
۲) \(1\)
۳) \(2\)
۴) \(3\)
۵۷. کدام عدد از بقیه کوچکتر است؟
۱) \(\sqrt[3]{81\times8\times5}\)
۲) \(\sqrt{50\times49}\)
۳) \(\sqrt[3]{9^2\times11^4}\)
۴) \(\sqrt{64\times242}\)
۵۸. با توجه به معادلهٔ زیر، حاصل \(10x+y\) چقدر است؟
\[\frac{8^{3-2x}\times125^{1-y}}{0.25^{y}\times16^{x+2}}=1.\]
۱) \(\frac{3}{10}\)
۲) \(4\)
۳) \(\frac{13}{10}\)
۴) \(13\)
۵۹. مجموع ریشه‌های معادلهٔ \(x^3-4x^2+3x=0\) چقدر است؟
۱) \(3\)
۲) \(4\)
۳) \(-3\)
۴) \(2\)
۶۰. کدام گزینه حاصل عبارت زیر است؟
\[\frac{3\sqrt[3]{16}-\big|-2\sqrt[3]{128}-\sqrt[3]{-250}\big|}{\sqrt[3]{108}}=\]
۱) \(\frac{1}{2}\sqrt[3]{4}\)
۲) \(\frac{\sqrt[3]{2}}{8}\)
۳) \(\frac{\sqrt[3]{4}}{8}\)
۴) \(\frac{-\sqrt[3]{2}}{4}\)
۶۱. اگر \(A\) و \(B\) به‌ترتیب مجموعه جواب نامعادله‌های \(\frac{2x}{5}-\frac{x}{3} < 2\) و \(6+4x > \frac{2(x-1)}{3}\) باشند، \(A\cap B\) کدام است؟
۱) \(\{x\mid 2 < x < 20\}\)
۲) \(\{x\mid\frac{2}{15} < x < 20\}\)
۳) \(\{x\mid-2 < x < 30\}\)
۴) \(\{x\mid-\frac{2}{15} < x < 30\}\)
۶۲. اگر \(2a^3 < 0\)، عبارت زیر برابر کدام گزینه است؟
\[\sqrt{a^2}+\sqrt[3]{a^3}+\sqrt[4]{a^4}+\dots+\sqrt[100]{a^{100}}\]
۱) \(100a\)
۲) \(a\)
۳) \(-a\)
۴) صفر
۶۳. حاصل عبارت زیر چیست؟
\[\frac{3}{\sqrt{5}+\sqrt{8}}+\frac{3}{\sqrt{8}+\sqrt{11}}+\dots+\frac{3}{\sqrt{35}+\sqrt{38}}\]
۱) \(\frac{\sqrt{5}-\sqrt{38}}{3}\)
۲) \(\sqrt{5}-\sqrt{38}\)
۳) \(\frac{\sqrt{38}-\sqrt{5}}{3}\)
۴) \(\sqrt{38}-\sqrt{5}\)
۶۴. کدام‌یک از چندجمله‌ای‌های زیر بر \(x+3\) بخش‌پذیر نیست؟
۱) \(x^3+2x^2-3x\)
۲) \(x^2+6x+9\)
۳) \(-4x^3-12x^2\)
۴) \(x^3-4x^2+4x\)
۶۵. اگر داشته باشیم \(A=\dfrac{n(n-2)}{n+3}+\dfrac{\frac{1}{n+3}}{\frac{1}{3n-6}}\)، حاصل \(A^3\) کدام گزینه است؟
۱) \(n^3-8\)
۲) \(n^3-6n^2+12n-8\)
۳) \(n^3+6n^2+12n-8\)
۴) \(n^3-6n^2+12n+8\)
۶۶. از برخورد سه خط \(x=-3\)، \(y=-4\)، و \(x+y=5\) یک مثلث ایجاد می‌شود. محیط این مثلث برابر با کدام گزینه است؟
۱) \(12+\sqrt{2}\)
۲) \(12(2+\sqrt{2})\)
۳) \(24\sqrt{2}\)
۴) \(48\)
۶۷. «ماشین رسّام» ماشینی است که براساس الگوریتم زیر کار می‌کند:
مرحلهٔ اول: مختصات یک نقطهٔ دلخواه مانند \(A\) را می‌گیرد.
مرحلهٔ دوم: محل نقطهٔ \(A\) را روی صفحهٔ مختصات می‌یابد.
مرحلهٔ سوم: از \(A\) به \(B\) (\(B\) قرینهٔ \(A\) نسبت به مبدأ مختصات است) وصل می‌کند.
مرحلهٔ چهارم: از \(B\)، \(2\) واحد به سمت پایین حرکت می‌کند و آن را \(C\) می‌نامد.
مرحلهٔ پنجم: معادلهٔ خط \(d\)، گذرنده از \(A\) و \(C\) را اعلام می‌کند.
اگر ورودی ماشین رسام \(A=\Big[{2\atop3}\Big]\) باشد، معادلهٔ خط \(d\) کدام است؟
۱) \(y=2x-1\)
۲) \(y=-3x-2\)
۳) \(y=2x-3\)
۴) \(y=-3x-4\)
۶۸. اگر \(A=\Big\{\Big[{x\atop y}\Big]\mid x^2=(y+3)^2\Big\}\)، کدام‌یک از نمودارهای زیر مجموعهٔ نقاط \(A\) را نشان می‌دهد؟
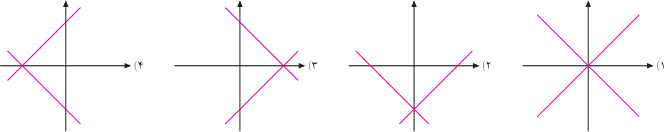
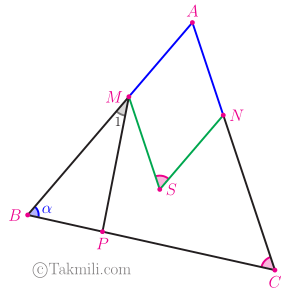
۶۹. با توجه به شکل زیر داریم \(AM=AN\)، \(MS=NS\)، و \(MP\) نیمساز زاویهٔ \(BMS\) است. زاویهٔ \(\alpha\) چقدر است؟ (\(\widehat{M}_1=29.5^\circ\) و \(\widehat{S}=\widehat{C}\))
۱) \(78^\circ\)
۲) \(85^\circ\)
۳) \(70^\circ\)
۴) \(62^\circ\)
۷۰. از مجذور کسری \(3\) برابر آن را کم کردیم، حاصل برابر \(-\frac{9}{4}\) شد. مجموع صورت و مخرج این کسر کدام‌یک از گزینه‌های زیر می‌تواند باشد؟
۱) \(5\)
۲) \(4\)
۳) \(-1\)
۴) \(-4\)
