۵۱. با توجه به عبارت‌های زیر، کدام گزینهٔ صحیح است؟
\[\begin{aligned}A&=25^{25}+3125^{10}+3\times5^{50}\\[8pt]B&=\frac{5^{1395}-5^{1397}}{2^{1397}-2^{1395}}\\[8pt]C&=2017^2-2015\times2017+2017\times2.\end{aligned}\]
۱) \(A > B > C\)
۲) \(A > C > B\)
۳) \(B > A > C\)
۴) \(C > A > B\)
۵۲. در مثلث قائم‌الزاویهٔ \(ABC\) \((\widehat{A}=90^\circ)\)، اگر زاویه‌ای که میانهٔ \(AM\) با وتر \(BC\) می‌سازد \(130^\circ\) باشد، اختلاف زاویهٔ \(B\) و زاویهٔ \(C\) چقدر است؟
۱) \(40\)
۲) \(35\)
۳) \(37\)
۴) \(32\)
۵۳. حاصل کدام کسر از بقیه کمتر است؟
۱) \(\dfrac{-2+\frac{2}{3}}{2+\frac{2}{3}}\)
۲) \(\dfrac{2+\frac{2}{3}}{\frac{2}{3}-2\frac{2}{3}}\)
۳) \(\dfrac{\frac{2}{3}}{2-\dfrac{\frac{2}{3}}{2+\frac{2}{3}}}\)
۴) \(\dfrac{2}{2-\dfrac{2}{2-\frac{2}{3}}}\)
۵۴. مثلث متساوی‌الاضلاع \(ABC\) مفروض است. اگر ارتفاع وارد بر قاعدهٔ \(BC\) را به‌اندازهٔ خودش امتداد دهیم تا به نقطهٔ \(D\) برسیم، مساحت مربعی که روی ضلع \(AB\) بنا می‌شود، چند برابر مساحت مثلث \(ABD\) خواهد بود؟
۱) \(\frac{2}{3}\sqrt{3}\)
۲) \(\frac{\sqrt{3}}{4}\)
۳) \(\frac{4}{3}\sqrt{3}\)
۴) \(3\sqrt{3}\)
۵۵. حاصل کسر زیر چیست؟
\[\frac{2}{51}+\frac{2}{47\times51}+\frac{2}{43\times47}+\dots+\frac{2}{7\times11}=?\]
۱) \(\frac{12}{119}\)
۲) \(\frac{44}{357}\)
۳) \(\frac{22}{357}\)
۴) \(\frac{1}{51}\)
۵۶. چند عدد اول کمتر از \(100\) وجود دارد که با یک مربع کامل، \(2\) واحد فاصله داشته باشد؟
۱) \(6\)
۲) \(5\)
۳) \(7\)
۴) \(8\)
۵۷. مقدار عددی عبارت \(\frac{b^2-3b}{ab-2a^2}\) به‌ازای \(a=-2\) و \(b=-3\) چقدر است؟
۱) \(0\)
۲) \(-9\)
۳) \(\frac{1}{9}\)
۴) \(-\frac{1}{9}\)
۵۸. در شش‌ضلعی منتظم زیر، مقدار \(9x-2y\) چقدر است؟
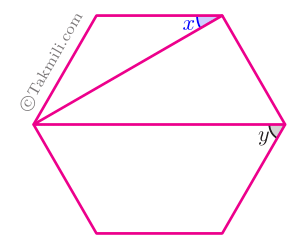
۱) \(90^\circ\)
۲) \(120^\circ\)
۳) \(150^\circ\)
۴) \(135^\circ\)
۵۹. مقدار \(x\) در معادلهٔ زیر چیست؟
\[\frac{\frac{3}{1+2x}}{\frac{1}{x-4}}=1\frac{3}{5}.\]
۱) \(-68\)
۲) \(60\)
۳) \(28\)
۴) \(-34\)
۶۰. می‌دانیم \(x=\frac{4+\sqrt{6}}{\sqrt{5}}\). در این صورت \(5x^2-\sqrt{24}\) برابر است با:
۱) \(9\sqrt{6}+\sqrt{5}\)
۲) \(22+6\sqrt{6}\)
۳) \(16\sqrt{6}\)
۴) \(5\sqrt{5}+\sqrt{6}\)
۶۱. مقدار \(B-A\) با توجه به شکل زیر کدام است؟
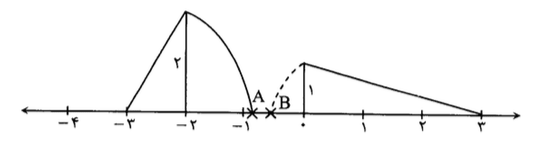
۱) \(6-\sqrt{10}-\sqrt{5}\)
۲) \(\sqrt{10}-\sqrt{5}\)
۳) \(\sqrt{10}-\sqrt{5}+6\)
۴) \(\sqrt{10}+\sqrt{5}\)
۶۲. کدام نقطه به مبدأ مختصات نزدیکتر است؟
۱) \(\Big[{0\atop4}\Big]\)
۲) \(\Big[{-5\atop0}\Big]\)
۳) \(\Big[{-3\atop3}\Big]\)
۴) \(\Big[{2\atop-3}\Big]\)
۶۳. یک ربات در نقطهٔ \(\Big[{-1\atop5}\Big]\) قرار دارد و طوری برنامه‌ریزی شده که با فرمان «حرکت» به اندازهٔ \((x-3)\overset{\rightarrow}{i}+4y\overset{\rightarrow}{j}\) جابه‌جا می‌شود. اگر بعد از \(3\) بار فرمان «حرکت» به نقطهٔ \(\Big[{8\atop11}\Big]\) رسیده باشد، مقدار \(x\) و \(y\) چقدر بوده است؟
۱) \(y=1\) و \(x=5\)
۲) \(y=2\) و \(x=9\)
۳) \(y=\frac{1}{2}\) و \(x=6\)
۴) \(y=3\) و \(x=3\)
۶۴. چندتا از گزاره‌های زیر درست است؟
\(\bullet\) اگر میانه و نیمساز نظیر یک رأس مثلثی برهم منطبق باشند، آنگاه این مثلث متساوی‌الساقین است.
\(\bullet\) مثلث قائم‌الزاویه‌ای وجود دارد که ارتفاع وارد بر وتر، نصف وتر باشد.
\(\bullet\) قطرهای هر پنج‌ضلعی با یکدیگر برابرند.
۱) \(1\)
۲) \(2\)
۳) \(3\)
۴) صفر
۶۵. یک تاس چهاروجهی (شامل اعداد \(1\)، \(2\)، \(3\)، و \(4\)) و یک تاس شش‌وجهی (شامل اعداد \(1\)، \(2\)، \(3\)، \(4\)، \(5\)، و \(6\)) را باهم پرتاب می‌کنیم. احتمال اینکه حداقل یکی از تاس‌ها عدد اول نشان دهد، چقدر است؟
۱) \(\frac{5}{8}\)
۲) \(\frac{1}{8}\)
۳) \(\frac{2}{3}\)
۴) \(\frac{3}{4}\)
۶۶. در شکل زیر، می‌دانیم مثلث \(ABC\) متساوی‌الساقین \((AB=AC)\) و چهارضلعی \(AMDN\) لوزی است. مثلث \(BDC\) چه نوع مثلثی است؟
۱) قائم‌الزاویه
۲) متساوی‌الاضلاع
۳) متساوی‌الساقین
۴) نمی‌توان تعیین کرد.
۶۷. چندتا از گزاره‌های زیر درست است؟
\(\bullet\) اگر \(m > 3\)، آنگاه \(1\times2\times\dots\times m+(m-2)\)، مرکب است.
\(\bullet\) اگر از مربع یک عدد فرد، یک واحد کم کنیم، حاصل بر \(4\) بخش‌پذیر است.
\(\bullet\) حاصل \(m(\sqrt{2}-\sqrt{3})(\sqrt{2}+\sqrt{3})\) همواره عددی گویا است.
۱) یک
۲) دو
۳) سه
۴) صفر
۶۸. اگر \(A=x^2-3\) و\(B=x^3+2x-7\)، \(A^2-Bx\) به‌ازای \(x=-3\) چه خواهد بود؟
۱) \(-43\)
۲) \(-84\)
۳) \(-72\)
۴) \(90\)
۶۹. میانگین \(11\) عدد فرد متوالی \(23\) است. میانگین سومین و هشتمین عدد چقدر است؟
۱) \(20\)
۲) \(21\)
۳) \(23\)
۴) \(22\)
۷۰. نقاط \(A\)، \(B\)، \(C\)، \(D\)، \(E\)، \(F\)، و \(G\) رئوس یک هفت‌ضلعی منتظم هستند. زاویهٔ بین امتداد \(AB\) و \(BC\) چقدر است؟
۱) \(80+\frac{120}{7}\)
۲) \(\frac{360}{7}\)
۳) \(\frac{540}{7}\)
۴) \(180-\frac{120}{7}\)
عالي