قضیهٔ نسبت در میانه های مثلث. در هر مثلث، میانهها به نسبت \(2\) به \(1\) یکدیگر را قطع میکنند.
اثبات. در مثلث \(ABC\) سه میانهٔ \(AM\)، \(BN\)، و \(CK\) را رسم میکنیم.
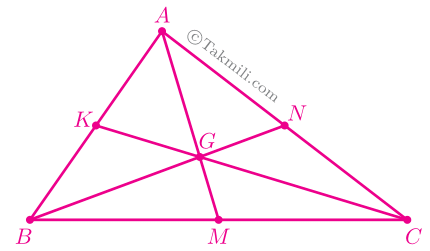
بنابه نتیجهٔ قضیهٔ همرسی میانهها، شش مثلث ایجاد شده در شکل بالا هممساحتاند. پس: \[\frac{S_{ACG}}{S_{CGM}}=\frac{2}{1}\cdot\quad(1)\] از \(C\) خطی بر \(AM\) عمود میکنیم و پای عمود را \(H\) مینامیم.
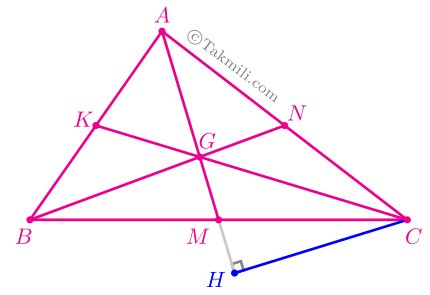
چون \(CH\) ارتفاع مثلثهای \(ACG\) و \(CGM\) است، پس داریم: \[\begin{aligned}\frac{S_{ACG}}{S_{CGM}}&=\frac{\frac{1}{2}CH\times AG}{\frac{1}{2}CH\times CM}\\[9pt]&=\frac{AG}{GM}.\quad(2)\end{aligned}\]
حال، از رابطههای \((1)\) و \((2)\) نتیجه میشود:\[\frac{AG}{GM}=\frac{2}{1}\cdot\] پس میانهها یکدیگر را به نسبت \(2\) به \(1\) قطع میکنند.


ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️در ضمن ممکنه اون ارتفاع از طرف دیگر رسم بشه بسته به اینکه کدوم زاویه منفرجه بشه درسته ؟؟؟
لطفا بگید @ادمین عزیز
راستی یک سوال ایا طول همه میانه ها برابر است ؟ چون تا حالا چیزی مبنی بر این گفته نشد
@@ادمین عزیز خواهشا پاسخ بدید
در جئوجبرا آزمایش کنید.
سلام توی مثلث متساوی الساقین هم اگر میانه وارد بر ضلع غیر ساق باشد انگاه چون عمود است نیازی به رسم پاره خط CH مثل این حالت نداریم درسته؟ یعنی تنها حالتی که راحت تر اثبات میشه در غیر این صورت باید رسم بشن بقیه درسته؟؟؟
میخواستم یک سوال بپرسم اگر روی مسئله این گونه باشد:
ثابت کنید در هر مثلث دوسر یک ضلع از میانه وارد بر آن ضلع به یک فاصله است این رو چطوری اثبات کنیم
برای مشاهدهٔ پاسخ این مسئله، اینجا را کلیک کنید.