در صورتی که کارشناسان سایت تکمیلی تشخیص دهند که مسئلهٔ شما قابلیت اضافه شدن به مسائل این صفحه را دارد، آن را (با پاسخ تشریحی) به مسائل سایت تکمیلی اضافه میکنند.
ریاضی هفتم
۲۹ مهر. دمای شهرهای کرمان، سنندج، و یاسوج بهترتیب \(11\) درجه بالای صفر، \(6\) درجه زیر صفر، و \(9\) درجه زیر صفر است. تعیین کنید سنندج چند درجه از میانگین دمای دو شهر کرمان و یاسوج سردتر است؟
۲۹ مهر. در مرکز یک شهر، سه ساختمان با ارتفاعهای متفاوت و نامهای زیر وجود دارد:
\(\bullet\) گالیله \((G)\)
\(\bullet\) اقلیدس \((E)\)
\(\bullet\) نیوتن \((N)\)
تنها یکی از گزارههای زیر دربارۀ این سه ساختمان درست است:
گزارهٔ ۱. نیوتن کوتاهترین ساختمان نیست.
گزارهٔ ۲. اقلیدس بلندترین ساختمان است.
گزارهٔ ۳. گالیله بلندترین ساختمان نیست.
این سه ساختمان را از کوچک به بزرگ مرتب کنید.
پاسخ تشریحی
۲۹ مهر. تعداد زیادی سکههای \(20\)، \(50\)، و \(100\) تومانی داریم. به چند حالت متفاوت میتوان پول یک جنس \(600\) تومانی را پرداخت؟
پاسخ تشریحی
۲۹ مهر. علی از محمد کوتاهتر است. مریم از مینا بلندتر است. محمد از مریم بلندتر است. سینا از مینا کوتاهتر است. چه کسی از بقیه قدبلندتر است؟
پاسخ تشریحی
۲۹ مهر. هریک از اعداد یک تا صد را با یکی از دو رنگ آبی و قرمز، رنگآمیزی میکنیم. میدانیم هیچ $7$ عدد متوالی، آبیرنگ نیستند. حداقل چند عدد را قرمز کردهایم؟
پاسخ تشریحی
۲۹ مهر. در یک گروه از مسابقات فوتبال، $4$ تیم وجود دارد که هریک با سه تیم دیگر گروه مسابقه میدهند. اگر نتیجهٔ بازی تساوی بود، هرکدام یک امتیاز کسب میکنند. اگر نتیجه تساوی نباشد، تیم برنده $3$ امتیاز و تیم بازنده صفر امتیاز میگیرد. در پایان مسابقات، مجموع امتیازات هر $4$ تیم، چند عدد مختلف میتواند باشد
پاسخ تشریحی
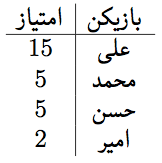
۲۴ مهر. علی، محمد، حسن، و امیر در یک بازی با هم مسابقه میدهند. هر دو بازیکن تنها یکبار با یکدیگر بازی میکنند. در آخر هر بازی، دو بازیکن یا مساوی میشوند یا یکی میبرد و دیگری میبازد. هر بازیکن برای هر برد، \(5\) امتیاز میگیرد، برای هر باخت \(0\) امتیاز و به ازای هر تساوی، \(2\) امتیاز میگیرد. کدام جدول (جدولهای) زیر برای توزیع امتیازات میتوانند امکانپذیر باشند؟



۲۰ مهر. پانزده کارت داریم. در یک طرف هر کارت، یک حرف انگلیسی و در طرف دیگر آن، یک عدد طبیعی نوشته شده است.

کمترین تعداد کارتی که لازم است پشت و رو شود تا مطمئن شویم که عبارت زیر درست است یا نه، چندتاست؟
«اگر در یک طرف یک کارت، حرف کوچک انگلیسی نوشته شده باشد، قطعاً در طرف دیگر آن یک عدد فرد نوشته شده است.»
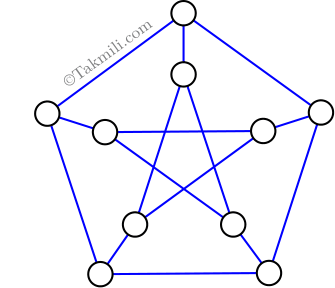
۱۹ مهر. در شکل زیر، میخواهیم دایرهها را طوری رنگ کنیم که هر دو دایرهای که با یک خط بههم وصل شدهاند، رنگهای متفاوتی داشته باشند. چنین کاری را حداقل با چند رنگ میتوان انجام داد؟
۱۶ مهر. دور یک دایره، \(26\) حرف الفبای انگلیسی را در جهت عقربههای ساعت مینویسیم. برای ایجاد پیام کد شده، برای هر حرف، \(4\) حرف در جهت عقربههای ساعت حرکت میکنیم و حرف را جایگزین میکنیم (به این روش، روش کدگذاری سزار گفته میشود). برای مثال، پیام \(ZAP\) به پیام \(DET\) کدگذاری میشود. حالت کدشدهٔ پیام \(WIN\) چیست؟
۱۵ مهر. با رسم سه خطّ راست، مستطیل زیر به پنج ناحیه تقسیم شده است. هریک از این ناحیهها یک چندضلعی هستند.

در اینجا، دو چندضلعی را همسایه مینامیم هرگاه این دو چندضلعی، ضلع مشترکی داشته باشند.
میخواهیم با رسم \(12\) خطّ راست، یک مستطیل را به چندتا چندضلعی تقسیم کنیم و سپس چندضلعیهای بهدست آمده را رنگ بزنیم بهطوریکه چندضلعیهایی که همسایهٔ یکدیگر هستند، رنگهای متفاوتی داشته باشند. برای این کار حداقل به چند رنگ نیاز داریم؟
۸ مهر. یک مدار عجیب شامل تعدادی سیم و تعدادی گره است که هر سه شرط زیر را داشته باشند.
\(\bullet\) هر سیم دو گره را بههم متصل کند.
\(\bullet\) بین هر دو گره، حداکثر یک سیم وجود داشته باشد.
\(\bullet\) هر گره دقیقاً به سهتا سیم متصل باشد.
شکل زیر، یک مدار عجیب با \(8\) گره و \(12\) سیم است.

اگر یک مدار عجیب \(13788\)تا سیم داشته باشد، آنوقت تعداد گرههای این مدار چندتاست؟
۸ مهر. سه جهانگرد خسته و کوفته به یک مهمانسرا رفتند. آنها بر سر یک میز نشستند و سفارش یک بشقاب کوفته برنجی دادند. تا پیشخدمت غذا را بیاورد هر سه چرتی کوتاه زدند. بعد از مدتی یکی از جهانگردها از خواب بیدار شد و \(\frac{1}{3}\) بشقاب را خورد و دوباره به خواب رفت. سپس دومی بیدار شد و غافل از اینکه دوستش غذا را خورده است، او هم \(\frac{1}{3}\) غذای باقیمانده را خورد و خوابید. آخر سر، جهانگرد سوم بیدار شد و \(\frac{1}{3}\) غذای باقیمانده را خورد. صبح روز بعد که پیشخدمت رستوران آمد، هشت عدد کوفته در بشقاب مانده بود. پیشخدمت چندتا کوفته برایشان آورده بوده است؟
۴ مهر. با ذکر دلیل مشخص کنید که یک خط راست، حداکثر از داخل چندتا از مربعهای کوچک شکل زیر، میتواند عبور میکند؟

پاسخ تشریحی
ریاضی هشتم
۲۹ مهر. مجموع دو عدد اول \(30\) شده است. آن دو عدد را پیدا کردیم. این مسئله چند جواب دارد؟
۲۹ مهر. فرض کنید \(n\) یک عدد طبیعی زوج باشد. اگر برای هریک از اعداد اول بزرگتر یا مساوی \(\frac{n}{2}\)، مانند \(p\)، عدد اولی مانند \(q\) وجود داشته باشد بهطوریکه \(p+q=n\)، آنوقت \(n\) را یک عدد زوج فراگُلدباخی مینامیم.
مثال ۱. عدد \(10\) یک عدد زوج فراگُلدباخی است. زیرا اعداد اول بزرگتر یا مساوی \(\frac{10}{2}\) عبارتند از: \[5,7\]و برای هریک از این دو عدد، یک عدد اول وجود دارد بهطوریکه مجموع آنها برابر \(10\) شود:\[\begin{aligned}5+5&=10\\7+3&=10.\end{aligned}\]مثال۲. عدد \(54\) یک عدد زوج فراگُلدباخی نیست. زیرا اعداد اول بزرگتر یا مساوی \(\frac{54}{2}\) عبارتند از:\[29,31,37,41,43,47,53\]و چون \(29+25=54\)، و \(25\) عدد اول نیست، پس \(54\) یک عدد زوج فراگُلدباخی نیست.
بهغیر از \(10\)، همهٔ اعداد زوج فراگُلدباخی کوچکتر از \(250\) را پیدا کنید.
۲۹ مهر. اگر اعداد طبیعی \(1\) تا \(22\) را درهم ضرب کنیم و سپس عدد حاصل را به عوامل اول تجزیه کنیم، توان عدد \(2\) در حاصلضرب چقدر است؟
۲۹ مهر. آقای اسماعیلی از همسایهاش، که ریاضیدانی بازنشسته است، در مورد ساکنین یک خانه میپرسد. همانطور که خواهیم دید، این پیرمرد موقر جوابهای چندان مناسبی نمیدهد.
آقای اسماعیلی میپرسد: «چند نفر در این خانه زندگی میکنند؟»
ریاضیدان: «سه نفر.»
آقای اسماعیلی: «چند سال دارند؟»
ریاضیدان: «نمیگویم. فقط میتوانم بگویم حاصلضرب سنشان \(1296\) است.»
آقای اسماعیلی: «خب، من هنوز نمیتوانم سن آنها را مشخص کنم.»
ریاضیدان: «مجموع سن آنها برابر شمارهٔ پلاک خانهٔ شماست. حالا چه میگویید؟»
آقای اسماعیلی که به دردسر افتاده است تلاش میکند معما را حل کند و میگوید: «هنوز نتوانستهام بفهمم افراد این خانه چند سال دارند.»
ریاضیدان: «آیا میدانید من چند سال دارم؟»
آقای اسماعیلی: «بله.»
ریاضیدان: «خب، هر سه از من کوچکترند.»
آقای اسماعیلی: «خیلی ممنون. حالا میدانم این سه نفر چند سال دارند.»
اختلاف سن بزرگترین و کوچکترین فرد آن خانه را بهدست آورید.
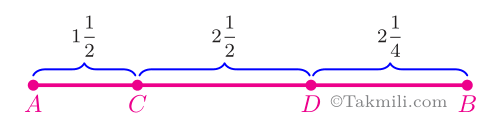
۲۹ مهر. شکل زیر، قسمتی از محور اعداد است و نقطهٔ \(A\) روی عدد \(-3\) قرار دارد. نقطههای \(M\) و \(N\) را بهترتیب وسط \(AD\) و \(AB\) قرار میدهیم. در اینصورت مقدار \(\frac{M}{N}\) را بیابید.
۲۹ مهر. حاصل عبارت زیر را بهدست آورید.
\[\frac{2}{5\times11}+\frac{2}{11\times17}+\frac{2}{17\times23}+\dots+\frac{2}{125\times131}\]
۲۴ مهر. حاصل کسر زیر را بهدست آورید.
\[\frac{5}{3\times8}+\frac{6}{8\times14}+\frac{7}{14\times21}+\dots+\frac{10}{38\times48}\]
۲۰ مهر. اگر \(40\) را بر نیم تقسیم کنیم و حاصل را با \(20\) جمع بزنیم، چه عددی بهدست میآید؟
پاسخ تشریحی
۱۹ مهر. فرید یک عدد را از بین اعداد \(6\)، \(5\)، \(4\)، \(3\)، \(2\)، \(1\)، \(0\)، \(-1\)، \(-2\)، \(-3\) و \(-4\) انتخاب میکند و سپس یک عدد دیگر انتخاب میکند که از عدد اولی بزرگتر است. چند جفت عدد با این شرایط میتواند انتخاب کند که مجموع آنها برابر \(3\) شود؟
پاسخ تشریحی
۸ مهر. محسن میخواهد یک تکه چوب را برش دهد تا به تکههای برابر تقسیم شود. در هر برش، یک تکه چوب به دو تکه تقسیم میشود؛ البته، محسن میتواند دو یا چند تکه چوب را کنار هم قرار دهد و ببُرد. برای مثال، برای تقسیم یک تکه چوب به \(5\) قسمت مساوی، کمترین تعداد برش، \(3\)تا است:

محسن میخواهد یک تکه چوب را به \(7\) قسمت مساوی تقسیم کند. او حداقل با چند برش میتواند این کار را انجام دهد؟
۴ مهر. الگوی عددی زیر را ببینید:

اگر الگوی بالا را ادامه دهیم، قطر اول این الگو، دنبالهٔ\[1,2,3,4,5,6,\dots\]است که از $1$ شروع میشود و هر عدد یک واحد از عدد قبلی بزرگتر است.
و قطر دوم این الگو، دنبالهٔ\[2,4,6,8,10,\dots\]است که از $2$ شروع میشود و هر عدد، دو واحد از عدد قبلی بزرگتر است.
بههمینترتیب، قطر $n$اُم این الگو با عدد $n$ شروع میشود و هر عدد $n$ واحد از عدد قبلی بزرگتر است.
عدد \(2021\) برای اولینبار در چندمین سطر افقی این الگو ظاهر میشود؟
ریاضی نهم
۳۰ مهر. میدانیم دو مجموعهٔ \(\{1,x-3,2\}\) و \(\{3,y,2\}\) برابرند. همهٔ مقادیر ممکن برای \(x\) و \(y\) را بیابید.
۲۹ مهر. شکل زیر، نمودار ون تعدادی از زیرمجموعههای متفاوت $\{1,2,3\}$ را نشان میدهد. کدام گزینه در مورد $A\cup D$ درست است؟
 ۱) میتواند دو عضوی باشد.
۱) میتواند دو عضوی باشد.
۲) حتماً یک عضوی است.
۳) میتواند سه عضوی باشد.
۴) این پنج مجموعه نمیتوانند متفاوت باشند.
۲۴ مهر. یازده زیرمجموعهٔ غیرمساوی از $M=\{1,2,3,\dots,10\}$ طوری انتخاب میکنیم که از هر دوتای آنها، یکی زیرمجموعهٔ دیگری باشد. اگر $A$، $B$، و $C$ بهترتیب مجموعههای $7$، $5$، و $3$ عضوی از این $11$ مجموعه باشد، در مورد $A\cup(B-C)$ چه میتوان گفت؟
۲۰ مهر. مریم یک عدد دو رقمی بهتصادف انتخاب کرده است. احتمال اینکه حاصلضرب ارقام آن عددی زوج باشد، چقدر است؟
۱۹ مهر. مجموعهٔ زیر را در نظر بگیرید:
\[X=\{0,1,2,3,4,5,6,7,8,9\}.\]به روشهای مختلفی میتوان اعضای این مجموعه را به دو یا چند زیرمجموعه تقسیم (اِفراز) کرد بهطوری که:
\(\bullet\) اشتراک هر دو زیرمجموعه تهی باشد،
\(\bullet\) اجتماع همه این زیرمجموعهها برابر \(X\) شود.
برای مثال، میتوان \(X\) را به چهار زیرمجموعه تقسیم کرد:
\[\begin{aligned}&\bullet\;\{0,3,4,5\}\\&\bullet\;\{2,9\}\\&\bullet\;\{7\}\\&\bullet\;\{1,6,8\}.\end{aligned}\]
مجموع اعداد هریک از زیرمجموعههای بالا برابر است با:
\[\begin{aligned}&\bullet\;0+3+4+5=12\\&\bullet\;2+9=11\\&\bullet\;7=7\\&\bullet\;1+6+8=15.\end{aligned}\]
با خواص گفته شده، به چند روش میتوان مجموعهٔ \(X\) را به دو یا چند زیرمجوعه تقسیم کرد بهطوریکه مجموع اعداد همهٔ زیرمجموعهها یکسان باشند؟
۱۶ مهر. اگر بدانیم که \(a\)، \(b\)، و \(c\) سه عدد حقیقی متفاوت هستند و \(\{b^2,a+1\}=\{3^2,-b^2,c\}\)، آنوقت چند مقدار مختلف برای \(a+b-c\) وجود دارد؟
پاسخ تشریحی
۱۵ مهر. در یک کیف تعدادی تیله با \(5\) رنگ مختلف وجود دارد. یک تیله را به صورت تصادفی انتخاب میکنیم. احتمال اینکه این تیله قهوهای باشد برابر \(0.3\) است. احتمال انتخاب تیلۀ قهوهای \(3\) برابر احتمال انتخاب تیلۀ بنفش، احتمال انتخاب تیلۀ سبز برابر احتمال انتخاب تیلۀ بنفش، و احتمال انتخاب تیلۀ قرمز برابر احتمال انتخاب تیلۀ زرد است. اگر یک تیله به تصادف از کیسه بیرون آوریم، چقدر احتمال دارد که این تیله قرمز یا سبز باشد؟
پاسخ تشریحی
۸ مهر. اگر $a$ و $b$ دو عدد حقیقی باشند و $\{b^2,a+1\}=\{9,-b^2\}$، آنگاه همهٔ مقدارهای ممکن برای $a+b$ را بیابید.
۴ مهر. \(10\) سنگ را از \(1\) تا \(10\) شمارهگذاری کردهایم:
\[1,2,3,4,5,6,7,8,9,10.\] میخواهیم این سنگها را در \(3\) گروه دستهبندی میکنیم بهطوری که مجموع هر گروه برابر \(11\) شود. به چند حالت میتوانیم این کار را انجام دهیم؟
برای مثال، یک حالت میتواند بهصورت زیر باشد:
\[\{1,10\},\{2,3,6\},\{4,7\}.\]


ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️سلام تکمیلی
درباره ی اینکه در طبیعت از منحنی فیبوناچی زیاد هست خیلی جا ها نوشته ، اما هیج جا درباره حرکت چیزی نگفته
وقتی یک سکه روی سطح صاف هل داده بشه ، تقریبا همون شکلی میشه