۸. ۳. ۲. ۱. در بازی مثلث که در بخش قبل معرفی شد،
الف) نفر اول چگونه بازی کند که همیشه برنده باشد؟
ب) فرض کنید بازی را با $n$ نقطه $(n>4)$ از رأسهای یک $n$-ضلعی منتظم انجام میدهید. برای چه $n$هایی نفر اول همیشه میتواند برنده باشد؟ برای چه $n$هایی نفر دوم میتواند همیشه برنده باشد؟
راهنمای حل
الف) شش نقطه را بهصورت زیر در نظر بگیرید.

نفر اول، پارهخط $AD$ را رسم میکند و نقطهٔ وسط آن را بهعنوان مرکز تقارنِ شکل (نقطهٔ $G$) در نظر میگیرد.
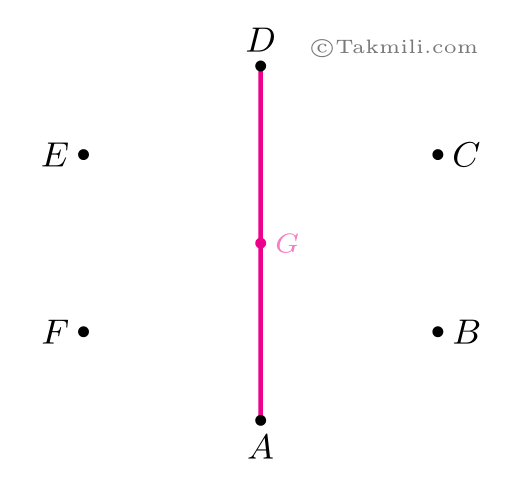
نفر دوم، هر پارهخطی را که رسم کرد، نفر اول قرینهٔ آن را (نسبت به نقطهٔ $G$) رسم میکند. برای مثال، اگر نفر دوم $AB$ را رسم کرد، نفر اول $DE$ را رسم میکند.
البته یک استثناء وجود دارد؛ اگر نفر دوم $CF$ یا $BE$ را رسم کرد، نفر اول $BE$ یا $CF$ را رسم میکند.
با روش گفته شده، واضح است که اگر نفر اول مثلثی رسم کرده باشد، قبل از او، نفر دوم مثلثی رسم کرده است.
ب) راهنمایی: برای $n$های زوجی که مضرب ۴ نیستند میتوان از روش قسمت «الف» استفاده کرد. برای $n$های مضرب ۴ نیز میتوان از روشی مشابه روش قسمت «الف» استفاده کرد.
نقد مسئله. در کتابهای تکمیلی، مسائلی مانند قسمت «ب» مسئلهٔ بالا، با عنوان «پروژه» معرفی شدهاند. در مورد این مسئله، یا نویسندگان کتاب فراموش کردهاند که عبارت «پروژه» را قبل از مسئله بنویسند یا ….


ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️سلام چرا نمی تونیم خط های مجاور رو انتخاب کنیم
سلام
متوجه منظورتان نشدم. کدام خطهای مجاور را انتخاب کنیم؟
سلام و شبتون بخیر
اگر نفر اول بتواند با 4k+2تا نقطه، که k عدد طبیعی است، همیشه برنده است. نفر دوم چه شرایطی لازم دارد؟
سلام
اگر نفر اول بتواند برنده شود، نفر دوم نمیتواند برنده شود!
نه منظورم این است که اگر نفر اول با n=4k+2 میتواند برنده شود. نفر دوم با چه nهایی؟
اصلاح . برای چند ضلعی های زوج هم میتواند نفر اول برنده باشد . پس نمی توان نظری داد همه چیز به حرکت 2 بازیکن برمیگردد . وقت بخیر
گفتم . برای چند ضلعی های زوج نفر اول به هر روشی بازی کند برنده هست . اما برای چندضلعی های فرد روش قطعی نمی توان داد چون همه چیز برمیگردد به اینکه نفر دوم چه حرکتی انجام بدهد.
الف) نفر اول و دوم اگر بدون خطا بازی کنند ؛ نفر اول همیشه برنده است چون تعداد خطها در 6 ضلعی تا عدم تشکیل مثلث فرد هست ، همینطور برای چند ضلعی های زوج .
اما برای چند ضلعی های فرد هم میتواند زوج بشود هم فرد تعداد خطها و هر دو احتمال برد دارند
باید روشی بدهید که حتماً نفر اول برنده شود.
اگر تا قبل از کشیدن آخرین پارهخط هیچ مثلثی تشکیل نشود، آنوقت میتوان دربارهٔ درستی یا نادرستی راهحل شما بحث کرد.
سلام، تشکر، سپاس بابت پاسخگویی.
ولی مثلث EFCیک رنگ نیست. دو ضلع نفر دوم و یک ضلع نفر اول است. وقتی کسی می بازد که مثلث یک رنگ تشکیل شود.
تشکر، سپاس
سلام
در کدام قسمت شرایط این بازی دربارهٔ رنگ چیزی نوشته شده است؟
سلام، وقت بخیر
اگر نفر اول، با طرح شما شروع کند ، نفر اول می تواند بازنده باشد. مثلاً مراحل زیر را دنبال کنید.
نفر اول: DA:CB:DC:FC::FB
نفر دوم:EF:FA:EB:EC
نفر اول به مثلث FCB می رسد. که بازنده است.
سلام
در مثال شما، وقتی نفر دوم EC را رسم میکند، میبازد. چون مثلث EFC تشکیل شده است.
سلام ببخشید یعنی در شش ضلعی نفر دوم نمیتواند با یک استراتژی بازی را ببرد ؟
سلام
خیر! اگر نفر اول درست بازی کند، نفر دوم نمیتواند برنده شود.
اگر میخواهید دربارهٔ بازیها و استراتژی برد بیشتر بدانید، در جلسهٔ پنجم کلاس دکتر علیپور شرکت کنید.
بنده این روش را با خودم بازی کردم ولی نفر دوم برنده شد چطور؟
وقتی نفر دوم پارهخط \(BC\) را میکشد، مثلث \(BCD\) ساخته میشود و میبازد! (پس از رسم پارهخط \(BC\) بازی تمام میشود.
سلام
قسمت ب گفتین که nهایی که مضرب ۴ هستن از روش مشابه استفاده میشود ممنون میشم این قسمت رو توضیح بدین ?
سلام
یعنی مانند حالت ششنقطه، ابتدا پارهخط وسط شکل را رسم کنید و سپس با قانون گفته شده، در هر مرحله، پارهخط متقارن نسبت به پارهخطی که نفر مقابل میکشد، رسم کنید.
لطفا جواب قسمت ب رو بزارید
قسمت «ب» مسئلهٔ سادهای نیست و همانطور که در نقد مسئله گفته شده، باید بهصورت پروژه میآمد. در تماسی هم که با نویسندهٔ این مسئله داشتهایم، ایشان موافق بودند و گفتند که متأسفانه، عنوان پروژه از این مسئله جامانده و همین که دانشآموزان برای چند مورد بررسی را انجام دهند، کفایت میکند. با راهنمایی گفته شده، میتوانید چند مورد را بررسی کنید.
میشه قسمت ب این تمرین رو توضیح بدین من متوجه نشدم…
این مسئله بسیار پیچیده است و مفصل است و نیاز به بحث در کلاس دارد. و در حد پروژههای کتابهای ریاضی تکمیلی است.
من از نویسندهٔ مسئله دربارهٔ آن پرسیدهام. او گفت که منظورشان این نبوده که برای همهٔ \(n\)های ممکن راهحل بیابید. همینکه برای چندتا \(n\) دانشآموز بتواند یکی استراتژی برد پیدا کند، کافی است.
و از نویسندهٔ این سؤال خواستم که این را در صورت مسئله ذکر کنند؛ او گفت که اگر سمپاد بخواهد کتابها را ویرایش کند، همینکار را میکنیم ولی متأسفانه سمپاد در چندسال گذشته کتابها را عیناً مشابه سالهای گذشته چاپ میکند و سفارشی برای ویرایش آنها به ما نداده است.
یعنی دقیقاً با این روش روی شش نقطه بازی کردید، و برنده نشدید؟
قبل از اینکه نفر اول \(BE\) را رسم کند، نفر دوم باخته است!
دقت کنید که وقتی یک نفر مثلث بکشد، بازی تمام میشود.
پس هنوز متوجه منظورتان نشدهام!
لطفاً این دو مثلث را نام ببرید.
و بازی را مرحله به مرحله شرح دهید؛ اینجوری:
نفر اول: \(AD\)
نفر دوم: \(CF\)
نفر اول: \(BE\)
.
.
.
شما صورت مسئله را بهدرستی متوجه نشدهاید.
لطفاً بازی مثلث را که در صفحهٔ قبلی این تمرین است، با دقت بخوانید.
در انتهای توضیحات بازی مثلث نوشته شده: «منظور از مثلث یک سهضلعی است که هر رأس آن یکی از شش نقطهٔ داده شده باشد.»
در راهحل بالا، ما برای درک بهتر راهحل، نقطهٔ \(G\) را اضافه کردهایم؛ و نقطهٔ \(G\) در صورت مسئله نیست!
سلام و خسته نباشید
ببخشین من متوجه توضیحات شما نمیشم گفتین که اگر نفر دوم CF یا BE را رسم کند، نفر اول هم BE یا CF را رسم می کند؟ میشه مججدا توضیح بدین
سلام
بهترتیب BE و CF در جمله بالا دقت کنید.
منظور این است که:
اگر نفر دوم CF را رسم کند، نفر اول BE را رسم میکند
و اگر نفر دوم BE را رسم کند، نفر اول CF را رسم میکند.
آهان خیلی ممنون
در صورت مسئله نگفته نقاط روی دایره هستند و یا تقارن دارند.
شش نقطه در «بازی مثلث» رسم شده است.
ببخشید میشه چند تا از جواب های قسمت ب رو بزارید
نفر اول n های فرد و نفر دوم n های زوج میتواند برنده شود در گل
فکر کنم منظورتون برعکس بوده! چون برای n=6 نشان دادیم که نفر اول همیشه برنده است.
باید استراتژی برنده شدن را دقیقاً مشخص کنید. در راهحل بالا، برای هر حرکت نفر دوم، حرکت نفر اول مشخص است.
روش شما باید بهگونهای باشد که اگر کسی آن را به زبان کامپیوتر بنویسد و یک بازی کامپیوتری تولید کند، کامپیوتر، در n های زوج اگر نفر اول باشد، همیشه برنده شود و در n های فرد اگر نفر دوم باشد، همیشه برنده شود.)
همان طور که گفتید قسمت الف نفر اول باید از قطرها شروع کند قسمت ب نفر اول n های فرد و نفر دوم n های زوج برنده است
میشه تا اونجا که به صورت تقریبی هم حل کردید تو سایت بزارید . به نظرم برای n های فرد هم نفر اول برنده هست قاعده خاصی ندارد. اما در 8 نقطه نفر دوم اول میشه بیشتر راهنمایی کنید چون واقعا کنجکاو شدیم
قسمت ب راه حل کلیش رو نمیزازید؟ فکر کنم چند جواب مختلف بیشتر نداشته باشد! منظورم مضرب عدد هاست
برای \(n\)های زوج، راهنمایی کردهایم.
برای \(n\)های فرد ما هنوز نتوانستهایم مسئله را کامل حل کنیم.
اگر شما توانستهاید مسئله را حل کنید، لطفاً پاسختان را برای ما بفرستید؛ اگر پاسخ شما درست بود بهنام خودتان همینجا قرار میدهیم و از امکانات رایگان سایت تکمیلی نیز بهرهمند خواهید شد.