در جدول زیر، رابطه‌ای که بین نُه عدد سمت چپ جدول برقرار است، بین نهُ عدد سمت راست جدول نیز برقرار است. به‌جای علامت‌های سؤال چه اعدادی باید قرار داد؟
به‌جای علامت سؤال سطر اول 49، به‌جای علامت سؤال سطر دوم 7، و به‌جای علامت سؤال سطر سوم 56 را باید قرار دهیم.
در نُه خانهٔ سمت چپِ جدول مضارب 3 و در نُه خانهٔ سمت راست جدول مضارب 7 قرار دارند. اگر اعداد را بهصورت زیر بنویسید، آنوقت بهسادگی تناظر بین اعداد سمت چپ و اعداد سمت راست جدول را میبینید.
بنابراین به‌جای علامت سؤال سطر اول $7\times 7$، به‌جای علامت سؤال سطر دوم $7\times 1$، و به‌جای علامت سؤال سطر سوم $7\times 8$ را باید قرار دهیم.
پاسخ، عدد 148 است.
در دنبالهٔ داده شده، هر عدد یک واحد از سه برابر عدد قبلیاش بیشتر است.
پاسخ، گزینهٔ C است.
در هر سطر، شکل سمت راست از رویهم قرار دادنِ شکل میانی و شکل سمت چپِ آن سطر بهدست میآید؛ با این شرط که نمادها یا خطوطی که رویهم میافتند حذف میشوند.
می‌دانیم یک عدد در الگوی اول به‌اشتباه نوشته شده است. همچنین، می‌دانیم یک عدد در الگوی دوم نیز به‌اشتباه نوشته شده است. اما می‌دانیم که اگر این دو عدد را باهم جابه‌جا کنیم، قانون هر دو الگوی عددیِ بالا درست می‌شود. این دو عدد کدام‌اند؟
اعداد 60 و 55 باید جابه‌جا شوند.
با روند زیر، هر عدد الگوی اول از عدد قبلیاش ساخته می‌شود:
\[+7,+14,+21,+28\]
با روند زیر، هر عدد الگوی دوم از عدد قبلیاش بهدست میآید:
\[+8,+16,+24,+32\]
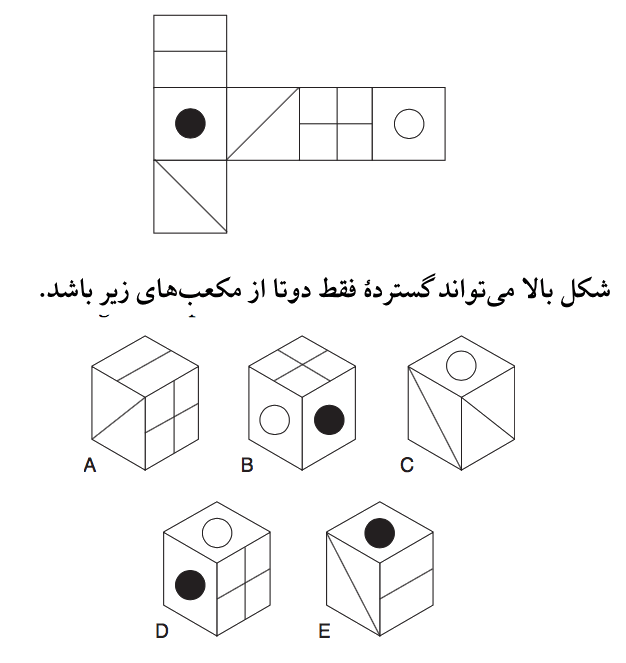
پاسخ، گزینهٔ B است.
نمادهای گزینهٔ B را باید در جای مشخص شده قرار داد.
کلید $A$ لامپ‌های ۱ و ۲ را «روشن-خاموش» یا «خاموش-روشن» می‌کند.
کلید $B$ لامپ‌های ۲ و ۴ را «روشن-خاموش» یا «خاموش-روشن» می‌کند.
کلید $C$ لامپ‌های ۱ و ۳ را «روشن-خاموش» یا «خاموش-روشن» می‌کند.
کلید $D$ لامپ‌های ۳ و ۴ را «روشن-خاموش» یا «خاموش-روشن» می‌کند.
پاسخ، گزینهٔ D است.
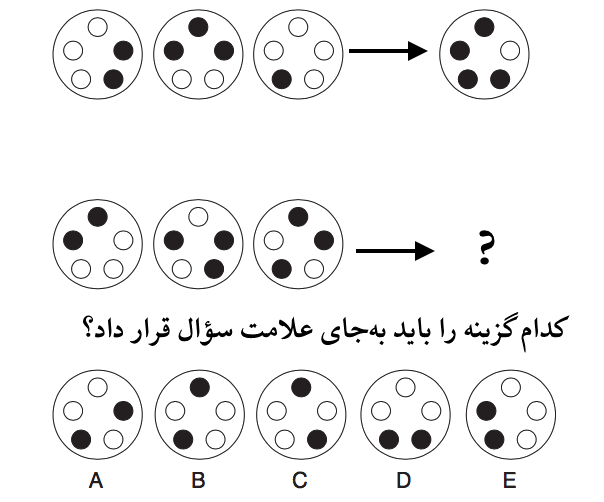
در مثال داده شده، به بالاترین نقطهٔ هریک از سه شکل سمت چپ نگاه کنید؛ دو نقطه سفید هستند و یک نقطه سیاه است. بنابراین بالاترین نقطهٔ شکل سمت راست، سیاه است. (نقطهای که یکبار در این جایگاه آمده در شکل سمت راست قرار میگیرد.)
دربارهٔ جایگاههای دیگر نیز همین قانون را بهکار میبریم.
پاسخ، گزینههای A و E است.
پاسخ، عدد 28917 است.
دو رقم از عدد سمت چپ انتخاب می‌کنیم بهطوریکه اگر با این دو رقم یک عدد دو رقمی بسازیم، رقمهای حاصلضرب این عدد دو رقمی در خودش، رقمهای دیگرِ عدد سمت چپ باشد. سپس، در سمت راست، ابتدا حاصلضرب عدد دو رقمی در خودش، و در ادامهٔ آن، عدد دو رقمی را مینویسیم.
\(\bullet\) در سطر اول، از عدد سمت چپ، رقمهای \(1\) و \(8\) را انتخاب می‌کنیم.
\[{\color{red}1}234{\color{red}8}\]
داریم:
\[18\times18={\color{blue}324}.\]
رقمهای \(3\)، \(2\)، و \(4\) در عدد سمت چپ موجود است. بنابراین، عدد سمت راست برابر است با:
\[{\color{blue}324}{\color{red}18}.\]
\(\bullet\) در سطر دوم، از عدد سمت چپ، رقمهای \(2\) و \(9\) را انتخاب می‌کنیم.
\[1{\color{red}2}48{\color{red}9}\]
داریم:
\[29\times29={\color{blue}841}.\]
رقمهای \(8\)، \(4\)، و \(1\) در عدد سمت چپ موجود است. بنابراین، عدد سمت راست برابر است با:
\[{\color{blue}841}{\color{red}29}.\]
\(\bullet\) در سطر سوم، از عدد سمت چپ، رقمهای \(2\) و \(4\) را انتخاب می‌کنیم.
\[{\color{red}24}567\]
داریم:
\[24\times24={\color{blue}576}.\]
رقمهای \(5\)، \(7\)، و \(6\) در عدد سمت چپ موجود است. بنابراین، عدد سمت راست برابر است با:
\[{\color{blue}576}{\color{red}24}.\]
\(\bullet\) در سطر چهام، از عدد سمت چپ، رقمهای \(1\) و \(7\) را انتخاب می‌کنیم.
\[{\color{red}1}2{\color{red}7}89\]
داریم:
\[17\times17={\color{blue}289}.\]
رقمهای \(2\)، \(8\)، و \(9\) در عدد سمت چپ موجود است. بنابراین، عدد سمت راست برابر است با:
\[{\color{blue}289}{\color{red}17}.\]
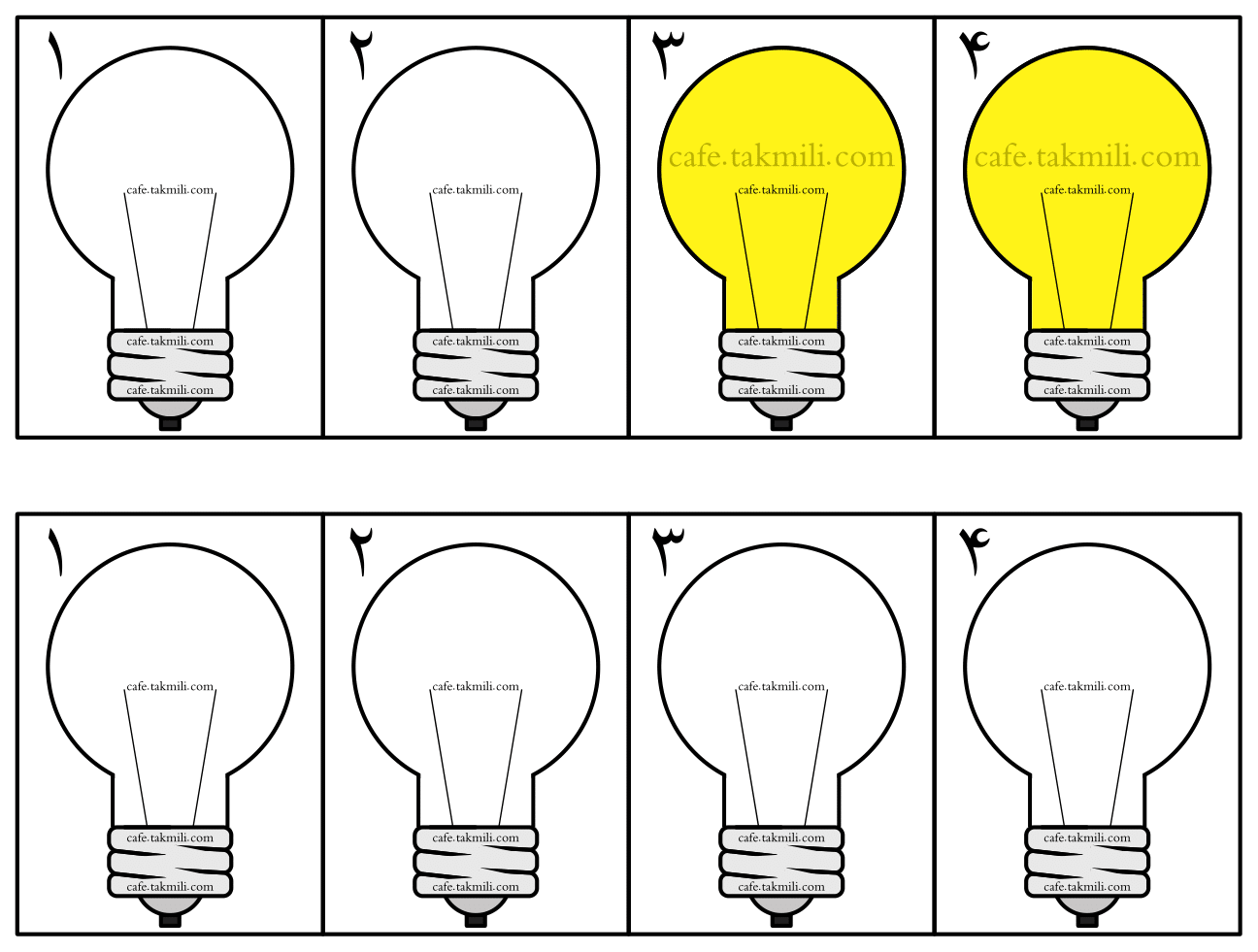کدام کلید کار نکرده است؟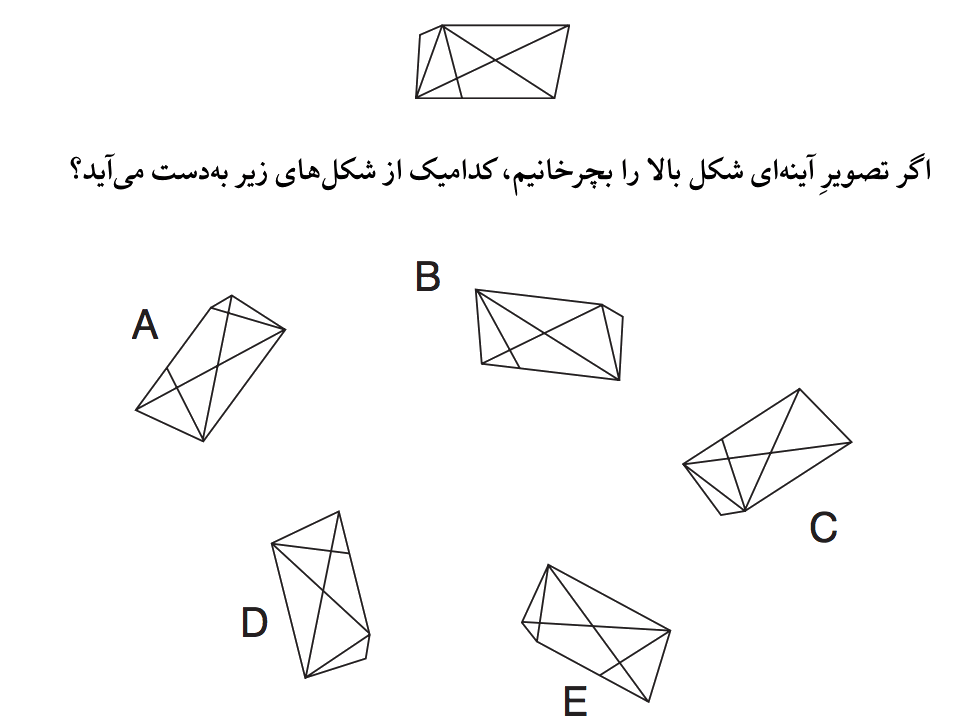
در بالا، اعداد سمت چپ علامت = را طوری داخل دایره‌ها قرار داده‌ایم که مجموع عددهایی که به هر دایره متصل‌اند، برابر عدد سمت راست علامت = باشد.
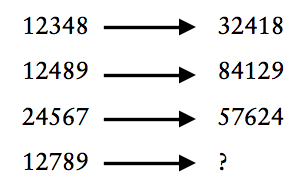به‌جای علامت سؤال، چه عدد باید قرار داد؟
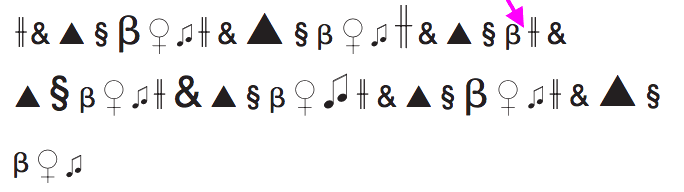
ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ می‌دهیم و بلافاصله یک ایمیل برایتان ارسال می‌کنیم. ❤️سلام،پاسخ سوال 7 اشتباه نیست؟؟؟؟؟
سلام.
به نظرم درست است. اگر شک دارید، تصویر شکل در موبایلتان را جلوی آینه بگیرید و بچرخانید!
ببخشید میشه سوال ۱۱ رو بیشترتوضیح بدید؟
این سؤال کمی سخت است! چون مشابه سؤال‌هایی که دیده‌ایم نیست.
به‌هرحال، راه‌حل این مسئله بازنویسی شد. لطفاً بخوانید و اگر همچنان واضح نبود، دقیقاً مشخص کنید که کدام قسمت راه‌حل را بیشتر توضیح دهیم.