به دنبالههایی عددی مانند دنبالهٔ\[11,13,15,17,19\]که جملهٔ دوم به بعد آن، از جمع زدن جملهٔ قبلی با مقدار ثابتی بهدست میآید، دنبالهٔ حسابی میگویند. در دنبالهٔ بالا، جملهٔ اول عدد \(11\) است و هریک از جملههای بعدی از جمع کردن عدد \(2\) با جملهٔ قبلی بهدست میآیند. مثال دیگری از دنبالهٔ حسابی:\[10,5,0,-5,-10,-15,\dots.\]
میخواهیم خانههای خالی جدول زیر را طوری پر کنیم که هر سطر آن (از چپ به راست) و هر ستون آن (از بالا به پایین)، یک دنبالهٔ حسابی باشد. همهٔ مقدارهای ممکن برای \(x\)، \(y\)، و \(z\) را بیابید.

راهنمای حل
خانههایی از جدول داده شده را بهصورت زیر نامگذاری میکنیم.
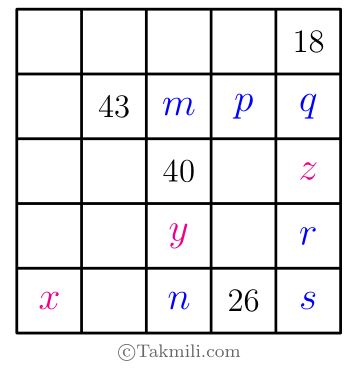
فرض کنیم که اختلاف \(y\) و \(40\) برابر \(d\) باشد، یا بهعبارتِدیگر، \(y=40+d\). دراینصورت، داریم:
\[\begin{aligned}n&=40+2d\\m&=40-d\\p&=37-2d\\q&=34-3d\\z&=50-6d\\r&=66-9d\\s&=82-12d.\end{aligned}\]
(چرا؟)
 حال، از سطر پنجم جدول بالا میتوان نتیجه گرفت که \(d=7\). (چگونه؟)
حال، از سطر پنجم جدول بالا میتوان نتیجه گرفت که \(d=7\). (چگونه؟)بنابراین:
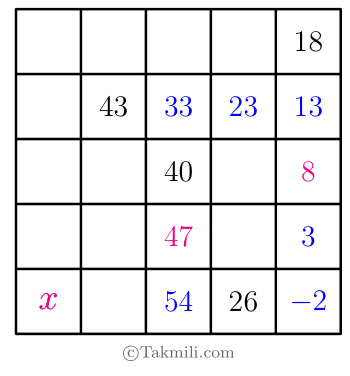 چون در سطر پنجم جدول بالا، هر عدد \(28\) واحد از عدد قبلیاش کمتر است، پس دومین و اولین عدد سطر پنجم، بهترتیب \(82\) و \(110\) هستند.
چون در سطر پنجم جدول بالا، هر عدد \(28\) واحد از عدد قبلیاش کمتر است، پس دومین و اولین عدد سطر پنجم، بهترتیب \(82\) و \(110\) هستند.
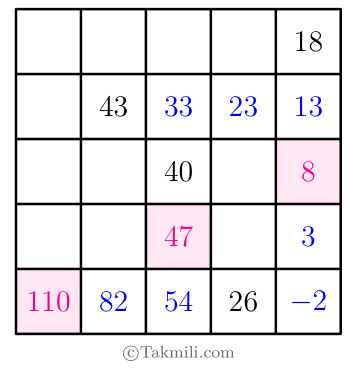 پس:
پس:
\[\begin{aligned}x&=110\\y&=47\\z&=8.\end{aligned}\]
توجه کنید که راهحل بالا نشان میدهد که بهجای هریک از نمادهای \(x\)، \(y\)، و \(z\) فقط یک مقدار میتوان قرار داد.
پرسش ۱. آیا میتوانید همهٔ خانههای خالی را با قانون گفته شده پر کنید؟
پرسش ۲. آیا میتوانید مسئلهای مشابه مسئلهٔ بالا طرح کنید که برای خانهٔ \(x\)، دقیقاً دو مقدار وجود داشته باشد؟
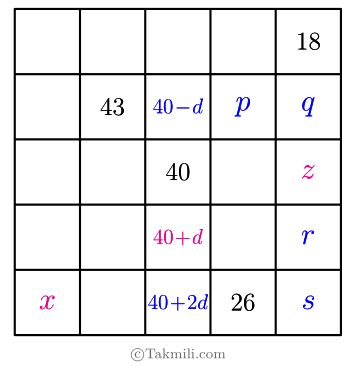 در سطر دوم، هر عدد باید با \(-3-d\) جمع شود تا عدد بعدی بهدست آید؛ زیرا:
در سطر دوم، هر عدد باید با \(-3-d\) جمع شود تا عدد بعدی بهدست آید؛ زیرا: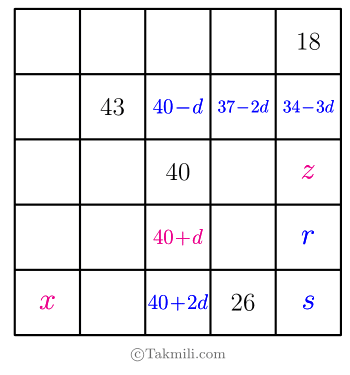


ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️