۱. مشابه تمرین ۴ صفحهٔ ۴ کتاب ریاضی هشتم
در دنبالهٔ \(1,3,9,4,11\) اختلاف هر دو عدد پشت‌سرهم را به‌دست می‌آوریم:
\[\begin{aligned}3-1=2,\;9-3=6,\;9-4=5,\;11-4=7.\end{aligned}\] در مثال بالا، کوچک‌ترین اختلاف بین دو عدد پشت‌سرهم، برابر \(2\) است.
الف) اعداد \(1,2,3,\dots,20\) را طوری جابه‌جا کنید که کوچک‌ترین اختلاف بین اعداد پشت‌سرهم، برابر \(10\) باشد.
ب) مریم اعداد \(1,2,3,\cdots,27\) را با ترتیبی دیگر پشت‌سرهم قرار داده است. سپس کوچک‌ترین اختلاف بین اعداد پشت‌سرهم را به‌دست آورده و آن را $M$ نامیده است. بزرگ‌ترین مقدار ممکن برای $M$ چیست؟ چرا؟
۲. مشابه تمرین ۱۴ صفحهٔ ۱۰ کتاب ریاضیات تکمیلی هشتم
می‌خواهیم خانه‌های خالی زیر را با اعداد \(2\)، \(4\)، \(6\)، \(8\)، \(10\)، \(12\)، \(14\)، و \(16\) پر کنیم به‌طوری‌که مجموع اعداد روی هر ضلع با مجموع اعداد روی هریک از دو ضلع دیگر برابر باشد. (تکرار اعداد مجاز نیست.)
اگر مجموع اعداد روی هر ضلع را با $S$ نمایش دهیم،
الف) آیا ممکن است \(S\) برابر \(28\) باشد؟ چرا؟
ب) آیا ممکن است \(S\) برابر \(36\) باشد؟ چرا؟
تمرین ۱۴ صفحهٔ ۱۰ کتاب ریاضیات تکمیلی هشتم
۳. مشابه تمرین ۹ صفحهٔ ۶ کتاب ریاضیات تکمیلی هشتم
الگوی عددی زیر را ببینید:
اگر الگوی بالا را ادامه دهیم، قطر اول این الگو، دنبالهٔ\[1,2,3,4,5,6,\dots\]است که از $1$ شروع می‌شود و هر عدد یک واحد از عدد قبلی بزرگ‌تر است.
قطر دوم این الگو، دنبالهٔ\[2,4,6,8,10,\dots\]است که از $2$ شروع می‌شود و هر عدد دو واحد از عدد قبلی بزرگ‌تر است.
به‌همین‌ترتیب، قطر $n$اُم این الگو با عدد $n$ شروع می‌شود و هر عدد $n$ واحد از عدد قبلی بزرگ‌تر است.
عدد \(1401\) برای اولین‌بار در چندمین سطر افقی این الگو ظاهر می‌شود؟
تمرین ۹ صفحهٔ ۶ کتاب ریاضیات تکمیلی هشتم
۴. مشابه تمرین ۹ صفحهٔ ۱۳ کتاب ریاضیات تکمیلی هشتم
فرض کنید \(p\) و \(q\) دو عدد طبیعی باشند به‌طوری‌که \[\frac{p}{q}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\dots-\frac{1}{1318}+\frac{1}{1319}.\] نشان دهید که \(p\) مضرب \(1979\) است.
تمرین ۹ صفحهٔ ۱۳ کتاب ریاضیات تکمیلی هشتم
۵. اینابا
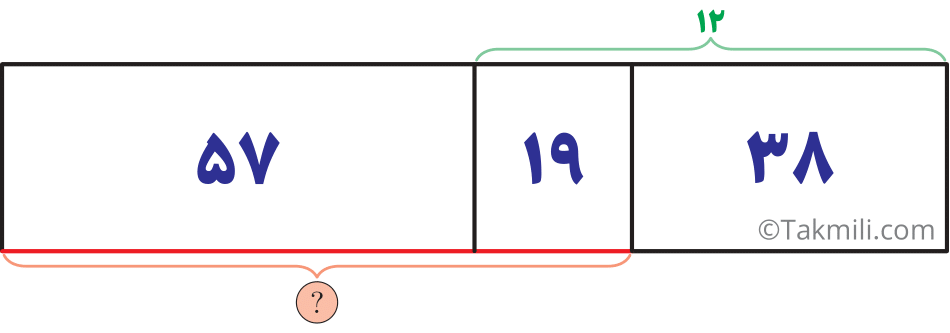
ابتدا مقدمهٔ کتاب اینابا را بخوانید. سپس، در شکل زیر، اندازهٔ ضلع خواسته شده را به‌دست آورید.
”
مقدمهٔ کتاب اینابا اینابا بیشتر!
۶. حاصل‌جمع‌های برابر
به روش‌های مختلفی می‌توان اعداد \(1\) تا \(9\) به دو یا چند دسته تقسیم کرد. برای مثال، می‌توان این اعداد را به سه دسته تقسیم کرد:
\[\begin{aligned}\{9,6\},\quad \{8,7\},\quad \{5,4,3,2,1\}.\end{aligned}\] مجموع اعداد هریک از دسته‌های بالا برابر \(15\) است.
اگر بخواهیم اعداد \(1\) تا \(9\) را به دو یا چند دسته تقسیم کنیم، به‌طوری‌که حاصل‌جمع همهٔ دسته‌ها یکسان باشد، آیا می‌توانید بگویید این حاصل‌جمع، چه اعدادی می‌تواند باشد؟
۷. چرخ رنگی!
مسیری به طول \(14\) متر شامل هفت ناحیهٔ یک‌متری آبی، و هفت ناحیهٔ یک‌متری قرمز است. ناحیه‌های آبی و قرمز، یکی‌درمیان هستند. چرخی دایره‌ای به شعاع \(2\) متر به‌صورت زیر در ابتدای مسیر قرار داده شده است. این چرخ به چهار ناحیهٔ برابر تقسیم شده است: دو ناحیهٔ آبی و دو ناحیهٔ قرمز.
وقتی چرخ دقیقاً یک دور کامل بچرخد (در جهت نشان داده شده در شکل بالا)، در چند درصد از مسیری که طی می‌کند، ناحیهٔ قرمز چرخ، ناحیهٔ قرمز مسیر را لمس می‌کند؟
۸. حدس کولاتز
درستی حدس کولاتز را برای اعداد \(134\) و \(226\) آزمایش کنید.
پرسش و پاسخ
سؤالاتتان دربارهٔ مسائل و محتوای تدریس شده در این جلسه را می‌توانید در بخش کامنت‌های زیر مطرح کنید.
