قضیهٔ ضضض. اگر سه ضلع از مثلثی با سه ضلع از مثلثی دیگر برابر باشد، آنگاه این دو مثلث همنهشتاند.
فرض. سه ضلع از مثلثی با سه ضلع از مثلثی دیگر برابر هستند.
حکم. این دو مثلث همنهشت هستند.
اثبات. فرض کنیم که در دو مثلث \(ABC\) و \(DEF\) داشته باشیم \(AB=DE\)، \(AC=DF\)، و \(BC=EF\). میخواهیم ثابت کنیم که دو مثلث \(ABC\) و \(DEF\) همنهشتاند.

یک نقطه مانند \(G\) میتوان یافت بهطوریکه \(G\) و \(B\) در دو طرف \(AC\) باشند و \(C\widehat{A}G=\widehat{D}\). روی نیمخط \(AG\) میتوان نقطهٔ \(H\) را طوری مشخص کرد که \[AH=DE.\quad(1)\].

پس بنابه حالت ضزض داریم: \[\begin{aligned}&\overset{\triangle}{DEF}\cong\overset{\triangle}{AHC}\quad(2)\\&EF=HC.\quad(3)\end{aligned}\]
سه حالت برای مثلثهای \(ABC\)، \(DEF\)، و \(AHC\) در نظر میگیریم:
حالت اول.
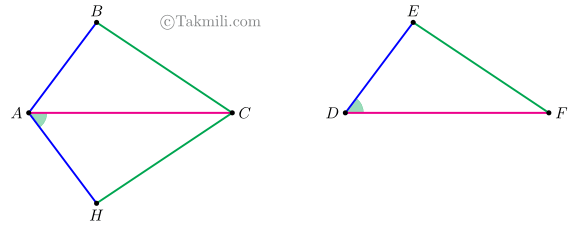
حالت دوم.
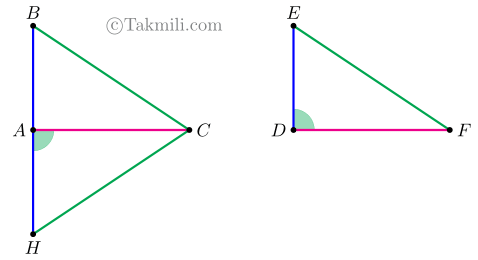
حالت سوم.
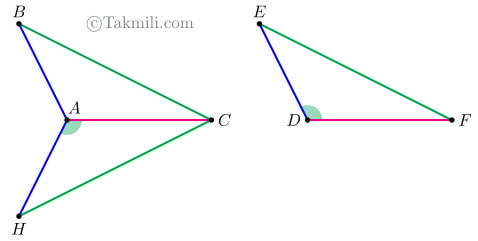
در هریک از سهحالت بالا، داریم:
\[\begin{aligned}&AB=AH\quad(4)\\&BC=HC.\quad(5)\end{aligned}\]
(چرا؟)
در هریک از حالتهای بالا ثابت میکنیم که دو مثلث \(ABC\) و \(AHC\) همنهشتاند.
اثبات حالت اول. \(B\) را به \(H\) وصل میکنیم.
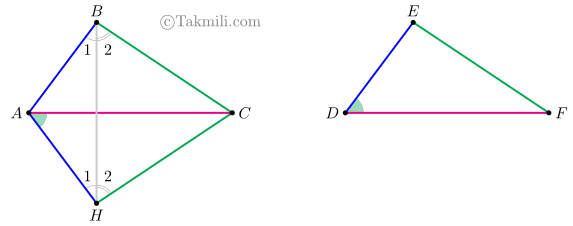
در مثلثهای \(ABH\) و \(CBH\)، بنابه قضیهٔ مثلث متساویالساقین داریم: \(\widehat{B}_1=\widehat{H}_1\) و \(\widehat{B}_2=\widehat{H}_2\). در نتیجه:
\[\begin{aligned}&\widehat{B}_1+\widehat{B}_2=\widehat{H}_1+\widehat{H}_2\\&\Rightarrow A\widehat{B}C=A\widehat{H}C.\quad(6)\end{aligned}\] پس بنابه حالت ضزض داریم: \[\overset{\triangle}{ABC}\cong\overset{\triangle}{AHC}.\quad(7)\] (چرا؟)
حال، از رابطههای \((2)\) و \((7)\) نتیجه میشود که دو مثلث \(ABC\) و \(DEF\) همنهشتاند.
اثبات حالت دوم. در این حالت، نقطههای \(B\)، \(A\)، و \(H\) روی یک خط قرار دارند. در مثلث \(BCH\)، بنابه قضیهٔ مثلث متساویالساقین داریم: \[C\widehat{B}A=C\widehat{H}A.\quad(8)\]
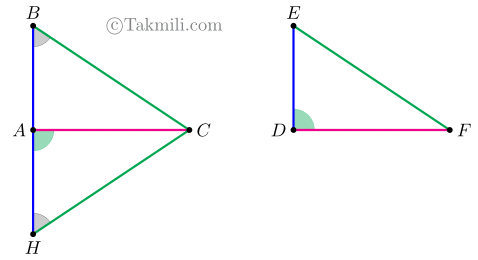
پس بنابه حالت ضزض داریم: \[\overset{\triangle}{ABC}\cong\overset{\triangle}{AHC}.\quad(9)\] (چرا؟)
حال، از رابطههای \((2)\) و \((9)\) نتیجه میشود که دو مثلث \(ABC\) و \(DEF\) همنهشتاند.
اثبات حالت سوم. \(B\) را به \(H\) وصل میکنیم. بنابه قضیهٔ مثلث متساویالساقین، در مثلثهای \(CBH\) و \(ABH\) داریم: \(C\widehat{B}H=C\widehat{H}B\) و \(\widehat{B}_2=\widehat{H}_2\). در نتیجه:
\[\begin{aligned}&C\widehat{B}H-\widehat{B}_2=C\widehat{H}B-\widehat{H}_2\\&\Rightarrow \widehat{B}_1=\widehat{H}_1.\quad(10)\end{aligned}\]
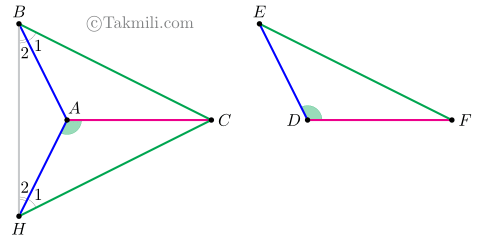
پس بنابه حالت ضزض داریم: \[\overset{\triangle}{ABC}\cong\overset{\triangle}{AHC}.\quad(11)\] (چرا؟)
حال، از رابطههای \((2)\) و \((11)\) نتیجه میشود که دو مثلث \(ABC\) و \(DEF\) همنهشتاند.
همانطور که دیدید برای اثبات همنهشتی مثلث ها در حالت سه ضلع از حالت ضزض و قضیهٔ مثلث متساویالساقین استفاده کردیم. توجه کنید که در قضیهٔ مثلث متساویالساقین، از قضیه ضضض استفاده نکردهایم.



ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️عالی
کدام گزینه از حالت های هم نهشتی مثلث نیست
۱)ض ض ض
۲)ز ز ز
۳) ض ز ض
۴)ز ض ز
۲ چون در حالت ۲ فقط متشابه میشن نه همنهشت چون میتونی مثلث بزرگتری از اون مثلث با همون مشخصات بکشی
سلام توی اثبات حالت دوم در واقع اون دو زاویه BAC,HAC هر دو 90 هستن یا به عبارت دیگه BAC=HAC=90 از طریق هم نهشتی درسته ؟؟؟
میشه بگید لطفا
اگر دو زاویه و محیط دو مثلث با هم برابر باشند هم نهشتی انها چگونه اثبات میشود
سؤال شما در صفحهٔ ۵۶ کتاب ریاضیات تکمیلی نهم آمده است. برای مشاهدهٔ پاسخ تشریحی آن، اینجا را کلیک کنید.
مفید بود ممنون
حالات هم نهشتی دو مثلث چیست
در حالتهای (قضیههای) همنهشتی، لازم نیست که برابری همهٔ شش جزء دو مثلث را بدانیم. مثلاً در حالت ضضض، اگر بدانیم سه ضلع از مثلثی با سه ضلع از مثلثی دیگر برابر باشد، آنگاه آن دو مثلث همنهشتاند؛ یعنی زاویههای آنها نیز نظیر به نظیر برابر خواهند بود.
بله. فقط نیاز به 3 جزء مثلث هست تا بفهمیم مثلث ها همنهشت هستند و در مثلث قائم الزاویه فقط تو جزء لازمه.
آیا اگر سه زاویه از مثلثی با سه زاویه از مثلث به دیگری نظیر به نظیر مساوی باشد آیا آنها هم نهشتند با داده
خیر!
برای مثال، در دو مثلث متساویالاضلاع غیر هماندازه، سه زاویه، نظیر به نظیر برابرند.
واقعا مرسی من واسه امتحانم اینو خوندم و کامل فهمیدم نمی دونم چجوری تشکر کنم واقعا
چرا در مثلث های قائم زاویه باید دو دلیل برای همنهشتی بودنشون پیدا کنیم انا در مثلث های عادی سه عامل باید برای همنهشت بودنشون پیدا کنیم
در مثلثهای قائمالزاویه هم، درواقع سهتا دلیل هست؛ و دلیل سوم همان زاویهٔ قائمه است!
سوال: اگر دو مثلث قائم و الزاویه وتر هایشان دلیل منطقی یا واضع نداشته باشیم علاوه بر اینکه بنا بر حالت وتر ویک ضلع و وتر ویک زاویه تند همنهشت نمیشود چرا؟ بنا به حالت سه ضلع هم همنهشت نیست.
یک سوال داشتم :در چه مثلث هایی به چند صورت می توان هم نهشتی آنها را مشخص کرد؟
در قضیههای هندسه، حالتهای همنهشی مثلثها و اثبات آنها نوشته شده است.
سلام،خیلی خيلی ممنون از حل خوبتون اما آیا روش ساده تری هم وجود داره؟؟؟؟
سلام . سوال ۳ صفحه ۹۵ ریاضی هشتم
سلام
آنچه در کتاب درسی نوشته شده درست است؛ اما سؤال ۳ صفحهٔ ۹۵ ریاضی هشتم، قضیهٔ ززض نیست! قضیهٔ ززض میگوید:
اگر دو زاویه و ضلع غیر بین آنها از یک مثلث با دو زاویه و ضلع غیر بین آنها از مثلث دیگر، نظیر به نظیر برابر باشند، آنگاه این دو مثلث همنهشتاند.
حتماً تمرین ۱۱ صفحهٔ ۹۸ کتاب ریاضیات تکمیلی هشتم را ببینید.
سلام مرسی آخه تو کتاب های درسی می نویسن حالت (ززض) اشتباهه
سلام
لطفاً بفرمایید که در کدام صفحهٔ کتاب درسی نوشته شده که حالت ززض اشتباه است.
سلام ببخشید آیا (ززض) جزو حالت های همنهشتی دو مثلث هست؟
سلام
بله! برای مشاهدهٔ اثبات حالت ززض، اینجا را کلیک کنید.
سلام . خسته نباشید. می تونیم دو ضلع EF و BC رو بر هم منطبق کنیم و از قوانین متوازی الاضلاع ها به هم نهشتی ایندو برسیم؟؟ بعد می تونیم نتیجه گیری کنیم که زاویه D با A برابر هست و هنمهشتی ایندو مثلث به صورت (ض ز ض) را ثابت کنیم.
سلام
نمیتونیم ضلعها رو بر هم منطبق کنیم! منطبق کردن ضلعها یعنی اینکه مثلثها رو حرکت بدیم. برای حرکت دادن مثلثها باید اصل یا تعریفی داشته باشیم، که در هندسهٔ اقلیدسی چنین اصولی را تعریف نکردهاند. این ایراد در توضیحات اصل ضزض شرح داده شده است؛ حتماً بخوانید.
مرسی لطف کردید.