نام کاربری و رمز عبور شما، شماره موبایل ارائه شده در زمان ثبت‌نام به همراه “0” اول شماره است.
لینک جلسات
مسائل هفتهٔ اول
از راه‌حل‌های تشریحی خود عکس بگیرید و آنها را در بخش کامنت‌های همین صفحه آپلود کنید.
- \(2009\) عدد که هر کدام برابر \(+1\) یا \(-1\) است دور یک دایره نوشته شده‌اند. در ضمن، همهٔ این عددها باهم برابر نیستند. برای هر \(10\) عدد متوالی، حاصل‌ضرب این \(10\) عدد را به‌دست می‌آوریم. حداکثر مقدار مجموع این حاصل‌ضرب‌ها را تعیین کنید.
- یک خط شکسته غیربسته و غیر خود متقاطع داده شده است که \(37\) ضلع دارد. خط گذرا از هر ضلع این خط شکسته را رسم می‌کنیم. حداقل تعداد خط‌های رسم‌شده را تعیین کنید.
- عدد \(2009\) دارای این ویژگی است که با جابه‌جایی رقم‌های آن، عدد چهاررقمی کوچکتر را نمی‌توان به‌دست آورد. اولین عدد بعد از \(2009\) که این ویژگی را دارد چند است؟
- شکل زیر را به \(8\) قسمت مشابه هم ببرید.
- در پارک درخت‌های کاج و افرا رشد کردند. \(60\) درصد کل درخت‌ها افرا بود. در بهار درخت‌های کاج نیز رشد کردند و پس از آن \(20\) درصد کل درخت‌ها افرا بود. مجدداً در پاییز تعدادی درخت افرا کاشته شد و \(60\) درصد کل درخت‌ها افرا بودند. طی یک‌سال تعداد درخت‌های پارک چند برابر شدند؟
- اگر یک اختاپوس تعداد زوجی پا داشته باشد راست می‌گوید و اگر تعداد فردی پا داشته باشد دروغ می‌گوید. یک‌بار اختاپوس سبز به اختاپوس آبی گفت: «من \(8\) پا دارم و تو \(6\) پا داری» و اختاپوس آبی جواب داد که من \(8\) پا دارم و تو \(7\) پا داری. اختاپوس بنفش وارد شد و گفت: «من \(9\) پا دارم و اختاپوس آبی \(8\) پا دارد». اختاپوس نارنجی وارد شد و گفت: «هیچ‌یک از شما \(8\) پا ندارید. فقط من \(8\) پا دارم». کدام اختاپوس \(8\) پا دارد؟
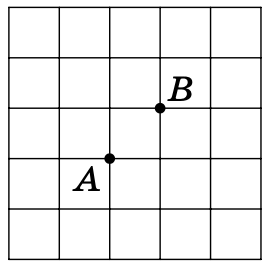
- یک گردشگر کنجکاو می‌خواد در خیابان‌های شهر از ایستگاه (نقطهٔ \(A\)) تا هتل (نقطهٔ \(B\)) قدم بزند. گردشگر دوست دارد مسیرش تا حد امکان طولانی باشد، اما علاقه‌ای ندارد که از یک تقاطع بیش از یک‌بار عبور کند. طولانی‌ترین مسیر ممکن را روی شکل مشخص کنید.
- یک شوالیه خسیس، سکه‌های طلا را در \(6\) صندوق نگه می‌دارد. یک روز هنگام شمارش آنها متوجه که اگر هر دو صندوق را باز کند می‌تواند سکه‌های موجود در آنها را به‌طور مساوی در این دو صندوق قرار دهد. او همچنین متوجه شده که اگر هر \(3\)، \(4\)، یا \(5\) صندوق را باز کند می‌تواند سکه‌های موجود در آنها را به‌گونه‌ای جابه‌جا کند که در تمام صندوق‌های باز به‌یک اندازه سکه وجود داشته باشد.
الف) آیا درست است که همهٔ سکه‌های موجود در \(6\) صندوق را می‌توان طوری جابه‌جا کرد که تعداد سکه‌های همه صندوق‌ها باهم برابر باشند؟
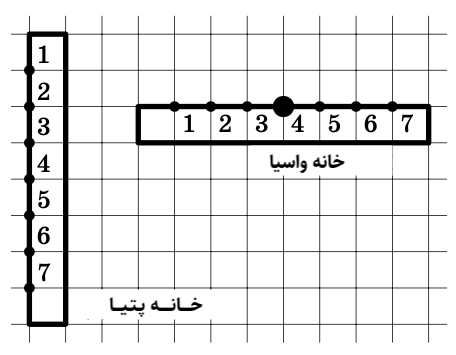
ب) اگر \(8\) صندوق وجود داشته باشد و شوالیه بتواند سکه‌های موجود در هر \(2\)، \(3\)، \(4\)، \(5\)، \(6\)، یا \(7\) صندوق را به‌طور مساوی بین خود این صندوق‌ها تقسیم کند، آیا درست است که سکه‌های همهٔ صندوق‌ها را نیز می‌تواند به‌طور مساوی بین \(8\) صندوق جابه‌جا کند؟ - پتیا و واسیا در دو خانه که در همسایگی یکدیگر قرار دارند، زندگی می‌کنند. خانه واسیا در ورودی چهارم قرار دارد. معلوم شد که پتیا برای رسیدن به خانه واسیا از کوتاهترین مسیر (نیازی نیست که از روی اضلاع شبکه حرکت کند) تفاوتی نمی‌کند که از کدام طرف، خانهٔ خود را دور بزند. مشخص کنید که خانهٔ پتیا در کدام ورودی قرار دارد؟
- در هریک از دو باغ، پدربزرگ به یک میزان شلغم کاشت. اگر نوه وارد باغ شود \(\frac{1}{3}\) شلغم‌های موجود در باغ را بیرون می‌آورد. اگر حشره وارد شود \(\frac{1}{7}\) شلغم‌های موجود در باغ را بیرون می‌آورد و اگر موش وارد شود \(\frac{1}{12}\) شلغم‌های موجود در باغ را بیرون می‌آورد. در پایان هفته، در باغ اول \(7\) شلغم و در باغ دوم \(4\) شلغم موجود بود. آیا حشره وارد باغ دوم شده است؟
- روی وتر \(AB\) از مثلث قائم‌الزاویهٔ \(ABC\)، نقطه \(K\) داده شده است به‌گونه‌ای که \(CK=BC\). خط \(CK\) نیم‌ساز \(AL\) را نصف می‌کند. زوایای مثلث \(ABC\) را تعیین کنید.
- در هر خانه از یک جدول \(101\times101\) غیر از خانهٔ مرکزی یکی از دو علامت «بپیچ» یا «مستقیم برو» قرار دارد. ماشین از خارج وارد یکی از خانه‌های مرزی جدول می‌شود و پس از آن به موازات اضلاع جدول طبق قوانین زیر حرکت می‌کند: ۱) اگر به‌خانه‌ای با علامت «مستقیم برو» برود، در همان جهتی که وارد این خانه شده به خانهٔ بعدی می‌رود و ۲) اگر به خانه‌ای با علامت «بپیچ» برود، \(90\) درجه می‌چرخد (به انتخاب خود یکی از دو جهت را در نظر می‌گیرد، و به خانهٔ بعدی می‌رود. آیا می‌توان علامت‌ها را به‌گونه‌ای گذاشت که ماشین به خانهٔ مرکزی نتواند برود؟
