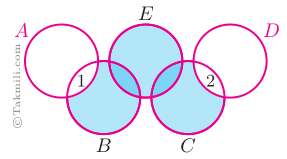
شکل زیر، نمودار ون تعدادی از زیرمجموعههای متفاوت $\{1,2,3\}$ را نشان میدهد. کدام گزینه در مورد $A\cup D$ درست است؟
 ۱) میتواند دو عضوی باشد.
۱) میتواند دو عضوی باشد.
۲) حتماً یک عضوی است.
۳) میتواند سه عضوی باشد.
۴) این پنج مجموعه نمیتوانند متفاوت باشند.
راهنمای حل (۱)
قرارداد برای نمودار ون
اگر نمودار ون دو مجموعهٔ \(X\) و \(Y\) بهصورت زیر رسم شده باشد، آنوقت هریک از سه ناحیهٔ نمودار (\(X-Y\)، \(Y-X\)، یا \(X\cap Y\)) میتواند تهی باشد یا نباشد.

اگر نمودار ون دو مجموعه \(X\) و \(Y\) بهصورت زیر رسم شده باشد، آنوقت این دو مجموعه مجزا هستند؛ یعنی اشتراک آنها حتماً تهی است. توجه کنید که در نمودار زیر، هریک از مجموعههای \(X\) یا \(Y\) میتوانند تهی باشند یا نباشند.
\(\bullet\) مجموعهٔ \(A\cup D\) میتواند دوعضوی باشد. (چرا؟)
\(\bullet\) مجموعهٔ \(A\cup D\) حتماً یکعضوی نیست. (چرا؟)
\(\bullet\) مجموعهٔ \(A\cup D\) نمیتواند سهعضوی باشد. (چرا؟)
\(\bullet\) این پنج مجموعه میتوانند متفاوت باشند. (چرا؟)
بنابراین، گزینهٔ ۱ درست است.
راهنمای حل (۲)
قرارداد برای نمودار ون
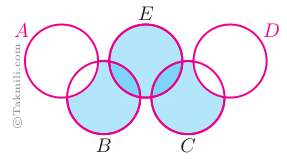
اگر نمودار ون دو مجموعه بهصورت زیر رسم شود، یعنی هیچیک از مجموعههای \(A-B\)، \(A\cap B\)، و \(B-A\) تهی نیستند.

با توجه به قرارداد بالا، در شکل زیر، \(A\) و \(D\) هریک باید دستکم دوعضوی باشند، اما سه مجموعهٔ دیگر هریک باید دستکم سهعضوی باشند. اما \(\{1,2,3\}\) تنها یک زیرمجموعهٔ سه عضوی دارد و نمیتوان سه زیرمجموعهٔ سهعضوی متفاوت از آن داشت. بنابراین، این پنج مجموعه نمیتوانند متفاوت باشند.

بنابراین، گزینهٔ ۴ درست است.
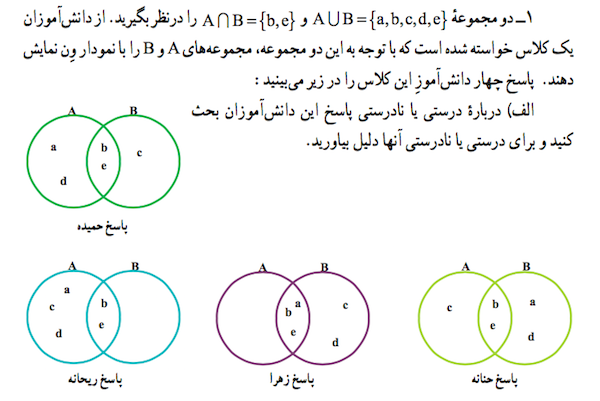
در کتاب ریاضی نهم، مشخص نشده که کدامیک از قراردادهای بالا را باید در نظر بگیریم. در فعالیت صفحهٔ ۱۲ کتاب ریاضی نهم، «پاسخ ریحانه» را ببینید. شما چگونه این مسئله را حل کردهاید؟ پاسخ ریحانه درست است یا نادرست؟
بد نیست بدانید که ریاضیدانها از نمودار ون برای اثباتهای دقیق خود استفاده نمیکنند.
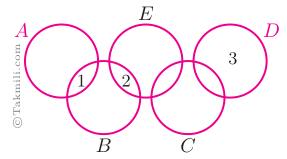


ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️سلام و خسته نباشید .
راهنمای حل یک درست چون در واقع اصلا نمودار ون برای نمایش مجموعه نیست این اشتباه خیلی رایج است . برای نمایش رابطه بین زیر مجموعه ها هست و چون زیر مجموعه خود یک مجموعه است به اصطلاح مجموعه A را به این شکل نشان می دهیم . یعنی اگر بخواهیم ساده بگوییم عضو های مجموعه اصلی را می نویسیم (بدون هیچ خم بسته ای) سپس هر خم بسته ای که می کشیم یک زیر مجموعه است . اگر در این خم بسته عضوی بود پس آن عضو آن مجموعه است (که در واقع زیر مجموعه است) اگر نبود تهی است. اگر با این دید صحیح نگاه کنیم کاملا از ابهام خارج می شویم .