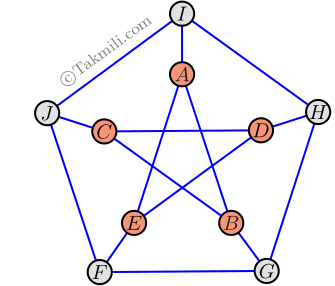
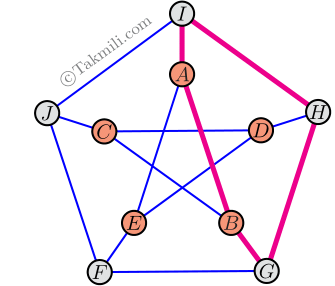
در نقشهٔ زیر، $10$ «شهر» با دایره‌های کوچک و $15$ «جاده» بین آنها با پاره‌خط نشان داده شده‌اند. منظور از یک «جاده»، پاره‌خطی مانند $AB$ است که دو رأس آن، روی دو شهر باشد. می‌دانیم که فقط در شهرها می‌توان از یک جاده به جادهٔ دیگر رفت.
با توجه‌به متن بالا، به پرسش زیر پاسخ دهید.
می‌خواهیم از شهر $A$ شروع به حرکت کنیم و در طول مسیر از هیچ جادهٔ تکراری رد نشویم و دوباره به شهر $A$ برگردیم. حداقل از چند جاده باید عبور کنیم؟
۱) $3$
۲) $4$
۳) $5$
۴) بیشتر از $5$
راهنمای حل
همهٔ شهرها را به‌صورت زیر نام‌گذاری می‌کنیم.
وقتی از \(A\) شروع به حرکت کنیم، یکی از سه شهر \(B\)، \(E\)، یا \(I\)، شهر بعدی خواهد بود. بنابراین، باید مسیرهایی را بررسی کنیم که با \(AB\)، \(AE\)، و \(AI\) شروع می‌شوند.
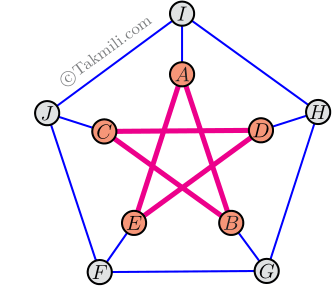
\(\bullet\) در بین همهٔ مسیرهایی که با \(AB\) شروع می‌شوند، طول کوتاهترین مسیر برابر \(5\) است. (چرا؟)
از شهر \(B\) فقط می‌توان به شهرهای \(C\) و \(G\) رفت. بنابراین، باید مسیرهایی را بررسی کنیم که با \(ABC\) و \(ABG\) شروع می‌شوند.
مسیرهایی که با \(ABC\) شروع می‌شوند
با توجه به شکل، پس از شهر \(C\)، فقط می‌توانیم به شهرهای \(D\) یا \(J\) برویم، در نتیجه، با یک بررسی ساده می‌توان فهمید که:
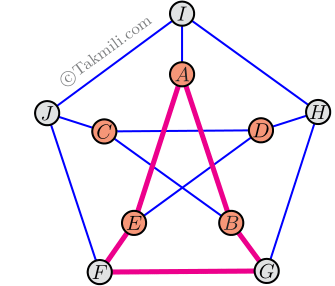
\(\blacktriangleleft\) در بین مسیرهایی که با \(ABCD\) شروع می‌شوند، \(ABCDEA\) کوتاهترین مسیر مورد نظر است.
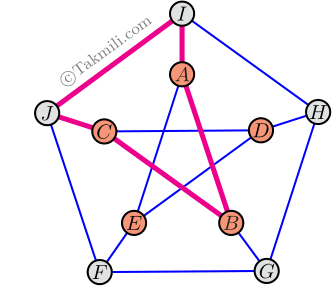
\(\blacktriangleleft\) در بین مسیرهایی که با \(ABCJ\) شروع می‌شوند، \(ABCJIA\) کوتاهترین مسیر مورد نظر است.
مسیرهایی که با \(ABG\) شروع می‌شوند
با توجه به شکل، پس از شهر \(G\)، فقط می‌توانیم به شهرهای \(F\) یا \(H\) برویم، در نتیجه، با یک بررسی ساده می‌توان فهمید که:
\(\blacktriangleleft\) در بین مسیرهایی که با \(ABGF\) شروع می‌شوند، \(ABGFEA\) کوتاهترین مسیر مورد نظر است.
\(\blacktriangleleft\) در بین مسیرهایی که با \(ABGH\) شروع می‌شوند، \(ABGHIA\) کوتاهترین مسیر مورد نظر است.
\(\bullet\) در بین همهٔ مسیرهایی که با \(AE\) شروع می‌شوند، طول کوتاهترین مسیر برابر \(5\) است. (چرا؟)
از شهر \(I\) فقط می‌توان به شهرهای \(H\) یا \(J\) رفت. به دلیل تقارن موجود در شکل، طول کوتاهترین مسیری که با \(AIH\) شروع میشود، با طول کوتاهترین مسیری که با \(AIJ\) شروع میشود، تفاوتی نخواهد داشت. پس فقط مسیرهایی را بررسی می‌کنیم که با \(AIH\) شروع می‌شوند.
از شهر \(H\) فقط می‌توان به شهرهای \(D\) یا \(G\) رفت. بنابراین، باید مسیرهایی را بررسی کنیم که با \(AIHD\) و \(AIHG\) شروع می‌شوند. با یک بررسی ساده می‌توان فهمید که:
\(\blacktriangleleft\) در بین مسیرهایی که با \(AIHD\) شروع می‌شوند، \(AIHDEA\) کوتاهترین مسیر مورد نظر است.
\(\blacktriangleleft\) در بین مسیرهایی که با \(AIHG\) شروع می‌شوند، \(AIHGBA\) کوتاهترین مسیر مورد نظر است.
بنابراین، گزینهٔ ۳ درست است.
شکل بالا، یکی از مشهورترین نمودارهای در ریاضیات است که به گراف پترسن مشهور است. گراف پترسن خواص بسیار جالبی دارد. طراح این مسئله، قطعاً با این گراف و خواص آن آشنایی کامل داشته که چنین سؤالی را طرح کرده است. از این گراف در تمرین ۸ صفحهٔ ۲۵ کتاب ریاضیات تکمیلی هشتم نیز استفاده شده است.
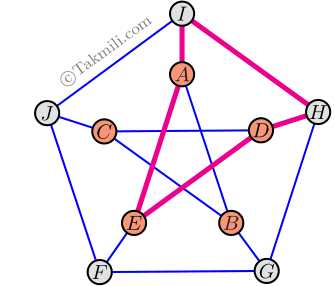
پرسش ۱. آیا می‌توانیم از شهر \(A\) شروع به حرکت کنیم و از هر جاده دقیقاً یک‌بار رد شویم و دوباره به شهر \(A\) برگردیم؟
پرسش ۲. می‌خواهیم از شهر $A$ شروع به حرکت کنیم و در طول مسیر از هیچ جادهٔ تکراری رد نشویم و دوباره به شهر $A$ برگردیم. حداکثر از چند جاده باید عبور کنیم؟
