- چند سهتایی مرتب مانند \((a,b,c)\) وجود دارد بهطوری که هریک از \(a\)، \(b\)، و \(c\) به مجموعهٔ
\(\{1,3,3^2,3^3,\dots,3^{10}\}\) تعلق داشته باشند و در ضمن، عدد \(a^b\times b^c\times c^a\) مربع کامل باشد؟ - به چند طریق میتوان \(4\) رأس از رأسهای یک \(11\)ضلعی منتظم را انتخاب کرد بهطوری که \(4\)ضلعی تشکیل شده توسط این \(4\) رأس، شامل مرکز \(11\)ضلعی نباشد؟
- در چند جایگشت دوری از اعداد \(1\) تا \(8\) هر دو عدد مجاور نسبت بههم اولاند؟
- تعداد دنبالههای \(a_1, a_2,\dots,a_6\) از عددهای طبیعی را بیابید بهگونهای که \(a_1=1\)، \(a_6=2310\)، و بهازای هر \(1\leq i\leq5\)، \(a_{i+1}\) بر \(a_i\) بخشپذیر باشد. در چند دنباله هیچ دوتا از \(a_i\)ها برابر نیستند؟
- خانههای بالای قطر اصلی یک جدول \(12\times12\) خاکستری و بقیهٔ خانههای جدول سفید شدهاند. میتوانیم سطرهای این جدول را باهم جابهجا کنیم. با تکرار این عمل، چند الگوی رنگی مختلف از قطر اصلی جدول میتوانیم بهدست آوریم؟
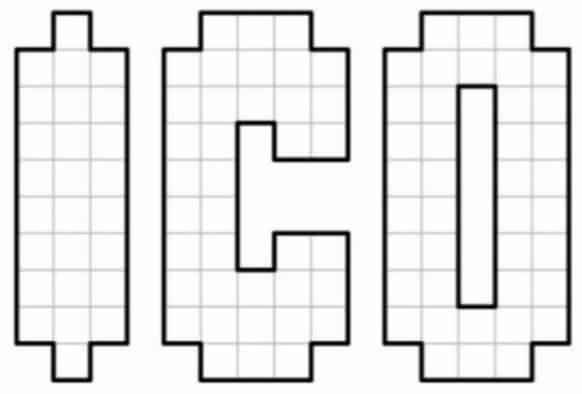
- به چند طریق میتوان با تعدادی دومینو، شکل زیر را بهطور کامل پوشاند بهطوری که هر خانه توسط یک دومینو پوشیده شود و هیچ دو دومینویی روی هم قرار نگیرند؟
- عدد طبیعی \(n\) را «خاص» میگوییم اگر عدد طبیعی \(m\) با ویژگیهای زیر وجود نداشته باشد:
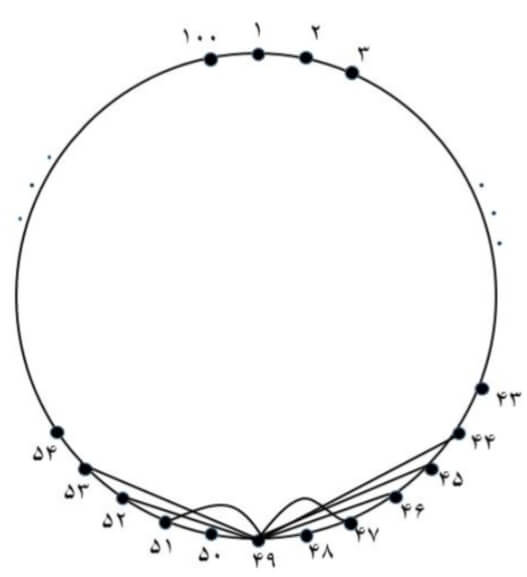
- یک دور \(100\) رأسی با شماره رأسهای \(1\) تا \(100\)، مانند شکل زیر، در اختیار داریم. میدانیم علاوه بر یالهای این دور، تعدادی یال دیگر مانند شکل، به رأس شمارهٔ \(49\) متصلاند. در این شکل چند مسیر متفاوت از رأس \(1\) به رأس شمارهٔ \(100\) داریم؟
- فرض کنید \(a_{n,k}\) تعداد راههای توزیع \(k\) آبنبات یکسان بین \(n\) نفر باشد بهگونهای که به هیچ کسی بیش از دو آبنبات نرسد. حاصل عبارت زیر را تعیین کنید.
- بهازای چند جایگشت از اعداد \(1\) تا \(30\) مانند \(a_1,a_2,\dots,a_{30}\) رابطهٔ \(\sum_{i=1}^{30}|a_i-i|=450\) برقرار است؟
- در چند جایگشت دوری از اعداد \(1,1,1,2,2,2,3,3,3\) سه عدد مجاور که همگی برابر باشند وجود ندارد؟

\(\bullet\) \(m > n\).
\(\bullet\) مجموع رقمهای \(m\) برابر مجموع رقمهای \(n\) باشد.
\(\bullet\) حاصلضرب رقمهای \(m\) برابر با حاصلضرب رقمهای \(n\) باشد.
چند عدد هفترقمی خاص وجود دارد؟
(منظور از یک رأس، نقاطیاند که دور دایره قرار دارند. منظور از یک یال، پارهخطی است که دو رأس را بههم متصل میکند.)
\[a_{2007,1}+a_{2007,4}+a_{2007,7}+\dots+a_{2007,4012}\]
اگر قبلاً «آنالیز ترکیبی ۴ (دورهٔ حل مسئله)» را خریدهاید، لطفاً وارد حساب کاربریتان شوید:
در غیر اینصورت، برای مشاهدهٔ بقیهٔ مسائل و راهحل تشریحی آنها، روی لینک زیر کلیک کنید و مراحل خرید محصول را انجام دهید.


ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️با سلام و عرض ادب و احترام
سوال۲ : راس های این ۱۱ ضلعی را به ترتیب از ۱ تا ۱۱ علامت گذاری کنیم اگر کوچک ترین راس انتخاب شده را k در نظر بگیریم ۳ ضلع بعدی باید حداکثر تا k+۵ انتخاب شوند پس تعداد حالت های مطلو ب برابرند با :
۱۱۰=۱۰×۱۱
سوال هفتم:
یک عدد خاص،نباید شامل ارقام مرکب باشد.مثلا عدد87 را در نظر بگیرید.چگونه یک m میسازید؟من عدد مورد نظرم را با تجزیه رقم8 میسازم و برای رسیدن به مجموع 15،از تعدادی رقم1 استفاده میکنم و به 42711 میرسم.این عدد هم از 87 بزرگتر است،هم مجموع ارقام آن با مجموع ارقام 87 برابر است و هم ضرب ارقام آن.پس نتیجه میگیریم یک عدد خاص باید و باید شامل ارقام1،2،3،5و7 باشد و بس.اکنون یک عدد خاص با ارقام غیر مرکب را در نظر بگیرید؛برای ساخت m،می توان همان ارقام عدد خاص را جابجا کرد،که این یعنی عدد خاص ما،باید بزرگترین عدد با آن مجموعه ارقام باشد،یا اگر عدد خاص مثلا شامل 2و3 بود،به جای آن دو،از رقم6 استفاده کرد که در این حالت مجموع ارقام افزایش می یابد.یا مثلا شامل دوتا 2 باشد که میتوان از یک 4 استفاده کرد که مجموع زیاد نمیشود ولی یک رقم از ارقام mکمتر میشود که مطلوب نیست.پس با داشتن مجموعه ارقام یک عدد خاص،آن عدد به طور یکتا مشخص میشود.مثلا،{7،1،12}عدد7211را مشخص می کند.زیرا گفتیم که بزرگترین عدد،مورد نظر است.اکنون تعداد مجموعه های رقم ها،متناظر است با جواب های معادله سیاله زیر در اعداد صحیح نامنفی:
X1+X2+X3+X4+X5=7
کهXiها تعداد ارقام1،2،3،5و7 هستند.و جواب این معادله هم برابر است با!11تقسیم بر!7×!4
سوال دهم:
هر ai و i یکی از اعداد 1تا30 است.پس اگر کل این اعداد از قدر مطلق خارج شوند،عددی به فرم زیر خواهیم داشت:
30 30 29 29 28 28…2 2 1 1
علامت های پشت این اعداد مجهول هستند و نمیدانیم کدامشان باید مثبت یا منفی باشند،ولی چون هر قدر مطلق،دقیقا یک عدد مثبت و یک عدد منفی به ما میدهد و ما 30 تا قدر مطلق داریم،پس باید دقیقا 30 عدد مثبت و دقیقا 30 عدد منفی داشته باشیم.(اگر aiوiبا هم مساوی باشند،باز هم میتوان فرض کرد یکی از دوعدد به صورت مثبت و دیگری به شکل منفی خارج میشود)اکنون میخواهیم برای مجموع بالا،یک ماکسیمم پیدا کنیم.به وضوح باید 30 علامت مثبت را برای جفت اعداد 16 تا 30 قرار دهیم و 30 علامت منفی را هم برای جفت اعداد 1 تا 15 تا به بیشترین مقدار ممکن برسیم.
این بیشترین مقدار ممکن همان عدد 450 است که طبق شرط،این مجموع باید برابر با آن می بود.از این موضوع نتیجه می گیریم که تمام جفت اعداد 16 تا 30 باید با علامت مثبت و تمام جفت اعداد 1 تا 15 باید با علامت منفی از قدر مطلق خارج شوند.و دوباره نتیجه میشود که برای این منظور،اعداد 1تا 15 باید در جایگاه های 16 ام تا 30 ام قرار بگیرند و اعداد 16 تا 30 هم باید در جایگاه های اول تا 15 ام قرار بگیرند.هر کدام از این دو گروه را به !15 حالت میتوان سازماندهی کرد و جواب نهایی طبق اصل ضرب برابر خواهد بود با:!15×!15
سوال چهارم:
جملات اول و ششم مشخص اند.جملات نامعلوم هم به وضوح مقسوم علیه ای از 2310 هستند.این عدد32 مقسوم علیه دارد.اگر مشخص کنیم که از کدام مقسوم علیه و چندتا از آن داشته باشیم،به طوری که در کل چهارتا مقسوم علیه انتخاب شوند،طبق شروط مسئله،دنباله به طور یکتا معین خواهد شد.پس جواب های مسئله،متناظر با جواب های معادله سیاله زیر در اعداد صحیح نامنفی اند:
X1+X2+…X32=4
که برابر است با!35تقسیم بر!4×!31.
حال اگر قرار نباشد که از عضو تکراری استفاده کنیم،محاسبه راحتتر میشود.هر چهار عضو مجهول،با یک زیر مجموعه چهار عضوی از مقسوم علیه های2310(به جز1و2310)متناظر میشوند که تعدادشان برابر است با ترکیب 4 از 30.
سوال سوم:
اعداد 2،4،6و8 نمی توانند کنار هم باشند و بین آنها به حداقل 4 عدد دیگر نیاز است.چون دقیقا چهار عدد 1،3،5و7 باقی مانده اند،هر کدام بین دو عدد قرار بگیرند،مقسوم علیه مشترکی جز عدد یک،با آن دو عدد مجاور نخواهند داشت…پس ابتدا اعداد2،4،6و8 را به!3و سپس اعداد 1،3،5و7 را بین چهار فضای خالی ایجاد شده و به!4حالت قرار میدهیم.پس پاسخ برابر است با!3×!4
با سلام و وقت بخیر…
سوال پنجم:
به جز خانه بالا چپ قطر اصلی که در هیچ حالتی،تغییر رنگ نمیدهد،بقیه خانه های این قطر به طور مستقل میتوانند خاکستری یا سفید بشوند.برای این منظور ابتدا مجموعه ای از خانه های قطر اصلی که میخواهیم خاکستری شوند را انتخاب میکنیم و با شروع از خانه ای که در پایین ترین سطر قرار دارد،جای آن سطر و سطر بالایی اش را عوض می کنیم.به این شکل رنگ خانه مد نظر خاکستری میشود.سپس به سراغ خانه بعدی می رویم و همین کار را تکرار میکنیم.پس میتوان به جز بالاترین خانه،رنگ همه خانه ها را تغییر داد.پس جواب طبق اصل ضرب برابر است با11^2=2048