مفهوم همنهشتی چندضلعی‌ها یکی از مفاهیم بسیار پیچیده برای دانش‌آموزان است. درک کامل این مفهوم نیاز به صرف زمان کافی و تمرین‌های زیاد دارد. متن زیر از کتاب «دربارهٔ استدلال‌های هندسی»، نوشتهٔ آ.ای. فه‌تیموف، انتخاب شده است.
یک روز در ابتدای سال تحصیلی، به گفتگوی دو دختر دانش‌آموز اول دبیرستان گوش می‌کردم. آنها دربارهٔ درس‌های تازه‌ای که داشتند بحث می‌کردند. دختر بزرگ‌تر، از درس هندسه با شگفتی یاد می‌کرد. او می‌گفت: درس بسیار عجیبی است. معلم وارد کلاس می‌شود، دو مثلث یکسان روی تخته رسم می‌کند، و در تمام طول ساعت تلاش می‌کند که همنهشتی آنها را برای ما ثابت کند. هیچ‌کس نمی‌فهمد که این تلاش بیهوده دربارهٔ اثبات مطلبی که واضح است، چه لزومی دارد…
بازی «تبدیل‌های هندسی و همنهشتی» می‌تواند به درک عمیق‌تر مفهوم همنهشتی کمک کند. در هر مرحله از این بازی، شکل وسط نشان‌دهندهٔ این است که دوران (چرخش) چندضلعی سمت چپ باید چگونه باشد. شما باید با توجه به دستور داده شده (شکل وسط)، پاره‌خط‌های چندضلعی سمت راست را طوری جابه‌جا کنید که یک چندضلعیِ همنهشت با چندضلعی سمت چپ به‌دست آید.
اگر کاربر سایت تکمیلی هستید،
وارد حساب کاربری‌تان شوید تا رکوردهای شما ثبت شود.
مفهوم ضلع‌ها و زاویه‌های نظیر در همنهشتی چندضلعی‌ها
می‌دانیم که یکی از مهم‌ترین اهداف تدریس هندسه، آموزش و تقویت استدلال منطقی است. در مبحث همنهشتی چندضلعی‌ها، نتیجهٔ آموزش اکثر کتاب‌های درسی و حتی برخی از معلمان این است که دانش‌آموزان صرفاً چند قضیه را حفظ می‌شوند و متأسفانه نمی‌توانند خودشان استدلال کنند!
در مبحث همنهشتی چندضلعی‌ها، تا وقتی که دانش‌آموز مفهوم «ضلع‌ها و زاویه‌های نظیر» (اجزاء نظیر) را عمیقاً درک نکرده باشد، مطمئناً فقط چند قضیه، مانند دو ضلع و زاویهٔ بین، دو زاویه و ضلع بین، سه ضلع، وتر و یک ضلع، یا وتر و یک زاویهٔ تند را حفظ کرده است.
وتر و یک زاویهٔ تند، و قضیهٔ ززض
«وتر و یک زاویهٔ تند» مسخره‌ترین قضیه در کتاب‌های درسی است!
«وتر و یک زاویهٔ تند» می‌گوید:
در دو مثلث قائم‌الزاویه، واضح است که زاویه‌های قائمه برابرند. اگر وتر و یک زاویهٔ تند یکی از این مثلث‌ها با وتر و یک زاویهٔ تند مثلث دیگر برابر باشد، آن‌وقت این دو مثلث همنهشت هستند.
در واقع، در دو مثلث فرض شده در «وتر و یک زاویهٔ تند»، دو زاویه (زاویهٔ قائمه و یک زاویهٔ تند) و ضلع غیر بین آنها (وتر) از یک مثلث با اجزاء نظیر از مثلث دیگر، برابرند.
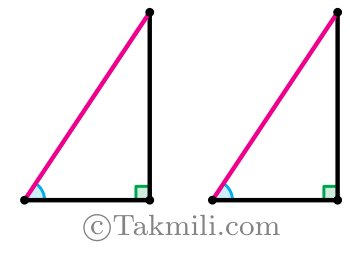
آیا چنین خاصیتی فقط در مثلث‌های قائم‌الزاویه برقرار است؟! یعنی اگر در دو مثلث دلخواه، دو زاویه و ضلع غیر بین یکی از مثلث‌ها با اجزاء نظیر آنها در مثلث دیگر برابر باشد، آن دو مثلث همنهشت نیستند؟!!
یکی از قضیه‌های مهم در همنهشتی مثلث‌ها، قضیهٔ ززض است.
قضیهٔ ززض می‌گوید:
اگر دو زاویه و ضلع غیر بین آنها از یک مثلث با دو زاویه و ضلع غیر بین آنها از مثلثی دیگر، نظیر به نظیر برابر باشند، آنگاه این دو مثلث همنهشتاند.
وقتی قضیهٔ ززض برای همهٔ مثلث‌ها برقرار است و اثبات آن نیز بسیار ساده است، چرا باید خودمان را به مثلث‌های قائم‌الزاویه محدود کنیم و این قضیه را در حالت خاص، وتر و یک زاویهٔ تند بنامیم؟!
قضیهٔ ززض در اکثر کتاب‌های درسی نیست. و توجه کنید که فقط در این قضیه است که باید نظیر به نظیر بودن ضلع‌ها و زاویه‌ها، دقیقاً بررسی شود. اگر کسی مفهوم ضلع‌ها و زاویه‌های متناظر را نداند، نمی‌تواند به‌درستی از قضیهٔ ززض استفاده کند. بنابراین، به معلمان و دانش‌آموزان اکیداً توصیه می‌شود که این قضیه را بیاموزند و از آن در تمرین‌ها استفاده کنند. در ادامه، تمرین‌هایی از کتاب‌های ریاضی تکمیلی آمده‌اند که به درک بهتر قضیهٔ ززض کمک می‌کنند.
تمرین ۱۱ صفحهٔ ۹۸ کتاب ریاضی تکمیلی هشتم. با ذکر دلیل مشخص کنید که کدام‌یک از عبارت‌های زیر همواره درست است و کدام‌یک همواره درست نیست.
الف) اگر دو زاویه و یک ضلع مثلثی با دو زاویه و یک ضلع از مثلث دیگر برابر باشند، آن دو مثلث همنهشتاند.
ب) اگر دو زاویه و یک ضلع از مثلثی با دو زاویه و یک ضلع از مثلث دیگر نظیر به نظیر برابر باشند، آن دو مثلث همنهشتاند.
تمرین ۴ صفحهٔ ۵۱ کتاب ریاضی تکمیلی نهم. چرا در قضیهٔ «ززض»، از عبارت «نظیر به نظیر» استفاده شده ولی در قضیهٔ «زض‌ز» از عبارت «نظیر به نظیر» استفاده نشده است؟
وتر و یک ضلع
توجه کنید که ایرادی که به «وتر و یک زاویهٔ تند» وارد کردیم، به قضیهٔ وتر و یک ضلع وارد نیست.
قضیهٔ وتر و یک ضلع می‌گوید:
در دو مثلث قائم‌الزاویه، واضح است که زاویه‌های قائمه برابرند. اگر وتر و یک ضلع یکی از این مثلث‌ها با وتر و یک ضلع مثلث دیگر برابر باشد، آن‌وقت این دو مثلث همنهشت هستند.
در واقع، در دو مثلث فرض شده در قضیهٔ وتر و یک ضلع، دو ضلع (وتر و یک ضلع قائم) و زاویهٔ غیر بین آنها (زاویهٔ قائمه) از یک مثلث با اجزاء نظیر از مثلث دیگر، برابرند. آیا چنین خاصیتی در مثلث‌هایی که قائم‌الزاویه نیستند نیز برقرار است؟ یعنی اگر در دو مثلث دلخواه، دو ضلع و زاویهٔ غیر بین یکی از مثلث‌ها با اجزاء نظیر آنها در مثلث دیگر برابر باشد، آن دو مثلث لزوماً همنهشت هستند؟
در تمرین ۱۲ صفحهٔ ۹۸ و تمرین ۱۳ صفحهٔ ۹۹ کتاب ریاضیات تکمیلی هشتم و تمرین ۵ صفحهٔ ۵۱ کتاب ریاضیات تکمیلی نهم، بحث‌های مفصلی دربارهٔ پرسش‌های بالا و قضیهٔ وتر و یک ضلع وجود دارد.
ممنون از لطف شما
سلام.وقت بخیر…
عذر میخوام؛بنده هفته گذشته برنده بخش بازیهای شما بودم،ولی تا اکنون هیچ پیامی از سایت تکمیلی دریافت نکردم.
ممنون.
سلام
هفتهٔ گذشته و این هفته برای شما ایمیل ارسال شده است:
هفتهٔ گذشته، پیامک هم ارسال شد. راهنمای حل مسائل ریاضی تکمیلی هشتم (به‌عنوان جایزهٔ بازی محاسبه) و راهنمای حل مسائل ریاضی تکمیلی نهم (به‌عنوان جایزهٔ بازی غلتاندن مکعب) فعال شده است.
با سپاس از همراهی شما