برای اینکه درسنامهٔ تقسیم چند جمله ای ها را بهخوبی بیاموزید، حتماً روی لینک زیر کلیک کنید و از روش ارائه شده در آن استفاده کنید.
چگونه درسنامههای سایت تکمیلی را بخوانیم؟
مثال ۱. حاصل هریک از تقسیمهای زیر را بهدست آورید و در هر مورد، درجهٔ یکجملهای حاصل را تعیین کنید.
الف) \(2x^2\) تقسیم بر \(x\)
ب) \(-\frac{3}{2}y^3\) تقسیم بر \(4y\)
ج) \(\sqrt{15}u^5\) تقسیم بر \(\sqrt{5}u\)

مثال ۲. اگر \(P(x)\) و \(Q(x)\) دوتا یکجملهای باشند و بدانیم \({\rm deg}\big(P(x)\big)=8\) و \({\rm deg}\big(Q(x)\big)=2\)، آنوقت حاصل هریک از عبارتهای زیر را بهدست آورید.
الف) \({\rm deg}\big(P(x)\div Q(x)\big)\)
ب) \({\rm deg}\Big(\big(P(x))^2\big)\div\big(2\big(Q(x)\big)^8\big)\Big)\)
تقسیم چندجملهایها
در زیر، الگوریتم تقسیم چندجملهایها را با استفاده از یک مثال، شرح میدهیم.
مـثال. چندجملهای $x^3+x+1$ را بر چندجملهای $x^2+1$ تقسیم کنید. خارجقسمت و باقیمانده را مشخص کنید و رابطهٔ تقسیم را بنویسید.
راهحل. به چندجملهای $x^3+x+1$ مقسوم و به چندجملهای $x^2+1$ مقسومعلیه میگویند. برای تقسیم چندجملهایها، مراحل زیر را بهترتیب انجام میدهیم.
مرحلهٔ اول. مقسوم و مقسومعلیه را استاندارد میکنیم. (خوشبختانه، در این مسئله هر دو استاندارد هستند!)
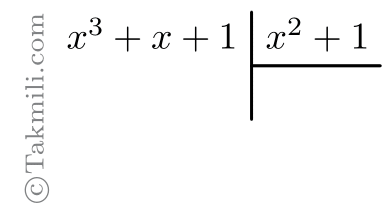 مرحلهٔ دوم. برای بهدست آوردن اولین جمله خارجقسمت، اولین جمله مقسوم را بر اولین جمله مقسومعلیه تقسیم میکنیم.
مرحلهٔ دوم. برای بهدست آوردن اولین جمله خارجقسمت، اولین جمله مقسوم را بر اولین جمله مقسومعلیه تقسیم میکنیم.
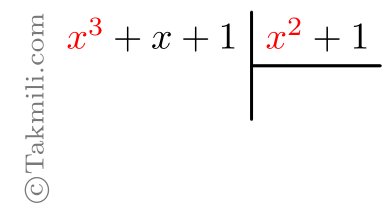
یعنی، \(x^3\) را بر \(x^2\) تقسیم میکنیم؛ حاصل برابر \(x\) میشود که آن را در خارجقسمت مینویسیم:
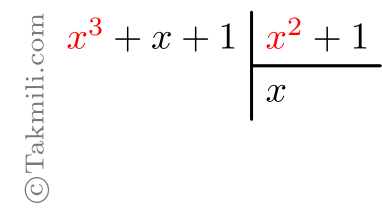
مرحلهٔ سوم. حاصل قسمت قبل را در مقسومعلیه ضرب میکنیم: \[x(x^2+1)=x^3+x.\]
مرحلهٔ چهارم. قرینهٔ حاصل قسمت قبل را زیر مقسوم مینویسیم.
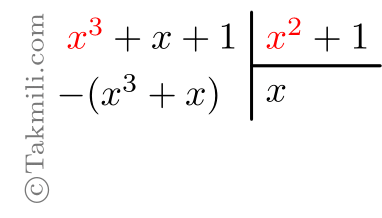
مرحلهٔ پنجم. ابتدا عبارت زیرِ مقسوم را قرینه میکنیم و سپس آن را با مقسوم جمع میزنیم.
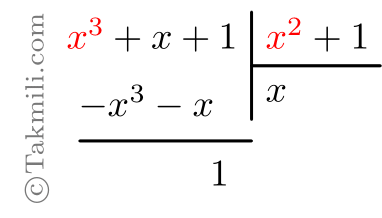
مرحلهٔ ششم. اگر درجهٔ چندجملهای حاصل از قسمت قبل (باقیمانده) از درجهٔ مقسومعلیه کمتر بود، به مرحلهٔ هفتم میرویم، و اگر نبود چندجملهای حاصل از قسمت قبل را مقسوم در نظر میگیریم و مرحلههای دوم تا ششم را انجام میدهیم.
در این مثال، چون \({\rm deg}(1) < {\rm deg}\big(x^2+1\big)\)، به مرحلهٔ هفتم میرویم.
مرحلهٔ هفتم. رابطهٔ تقسیم، یعنی:
باقیمانده \(+\) خارجقسمت \(\times\) مقسومعلیه \(=\) مقسوم
را مینویسیم و مقسوم، مقسومعلیه، و خارجقسمت را مشخص میکنیم.
\[x^3+x+1=(x^2+1)(x)+1.\]
مقسوم: \(x^3+x+1\)
مقسومعلیه: \(x^2+1\)
خارجقسمت: \(x\)
باقیمانده: \(1\)

در ویدئوی زیر، با یک مثال دیگر الگوریتم تقسیم چند جمله ای ها توضیح داده شده است.
برای دانلود ویدئوی بالا، اینجا را کلیک کنید.
مثال ۳. تقسیمهای زیر را انجام دهید و رابطهٔ تقسیم را برای هریک از آنها بنویسید.
الف) \((1+x^2+x)\div (1+x)\)
ب) \((-2+2x^3)\div(4x^2)\)
ج) \((x^8+2x^2+1)\div(2x^3-3)\)
د) \((-x^4+4x+x^2)\div(x-1)\)

مثال ۴. یک چندجملهای درجه \(5\) را بر یک چندجملهای درجه \(3\) تقسیم کردهایم. درجهٔ خارجقسمت چند است؟ چرا؟ یک مثال بزنید.
مثال ۵. هریک از تساویهای زیر، رابطهٔ یک تقسیم را نشان میدهد. ابتدا بهجای \(P(x)\) چندجملهای مناسب قرار دهید و سپس، مقسوم، مقسومعلیه، خارج قسمت، و باقیمانده را مشخص کنید.
الف) \(4x^5+1=\big(P(x)\big)\big(2x^2+2x+1\big)+\big(-x^2-2x+\frac{1}{2}\big)\)
ب) \(x^5+2x^2+1=\big(P(x)\big)\big(x^2-x+1\big)+x\)
شکل دیگر رابطهٔ تقسیم
\[F(x)=P(x)\times Q(x)+R(x).\]
رابطهٔ تقسیم را بهصورت زیر نیز میتوان نمایش داد:
\[\frac{F(x)}{P(x)}=Q(x)+\frac{R(x)}{P(x)}.\]
مثال ۶. چند عدد صحیح مانند \(n\) وجود دارد بهطوریکه حاصل عبارت زیر عددی طبیعی شود؟
\[\frac{3n^4-5n^3+3n^2-15n-11}{n^2+3}\]
زنگ تفریح
تمرینهای تقسیم چند جمله ای

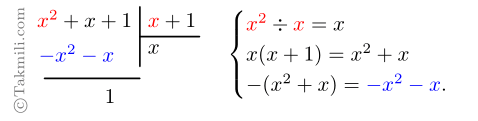
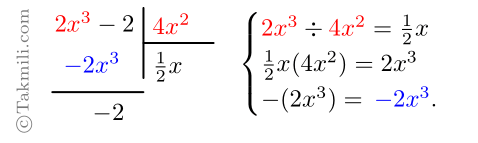
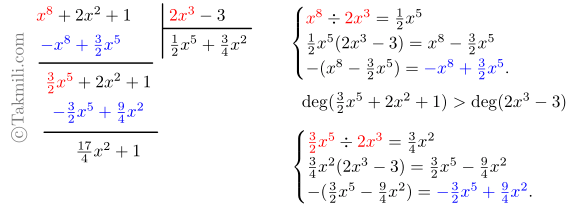
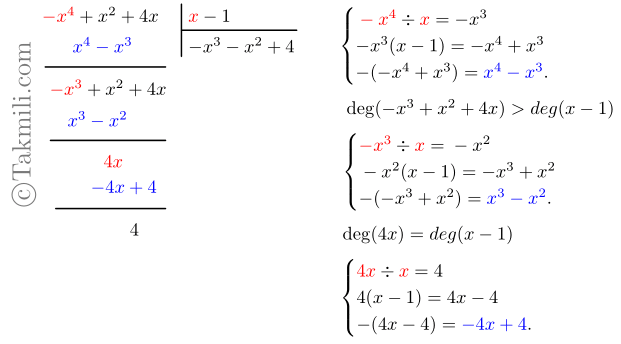
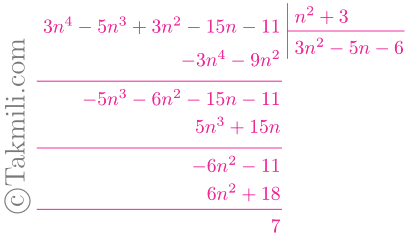



ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️سلام وقت بخیر
ببخشید میخواستم بپرسم که در تمامی این تقسیماتی که ما انجام داده ایم، مشکل تقسیم بر صفر را چه کنیم؟ میدانم که متغیر با “مجهول” و “جانگهدار” مفهومی متفاوت دارد اما حتی اگر داشته باشد، شما گفته اید که هر کدام از این تقسیمات، یک اتحاد هستند. اما اگر برای مثال مقسومعلیه ما $x^2 + x$ باشد و در شرایطی، این عبارت برابر با صفر شود، دیگر اتحاد بودن تساوی، غلط میشود. ممنون میشم اگر این قضیه را برایم توضیح دهید
اون تساوی، رابطهٔ تقسیم است:
باقیمانده \(+\) خارجقسمت \(\times\) مقسومعلیه \(=\) مقسوم
آیا اگر مقسومعلیه صفر شود، اتحاد بودن تساوی بالا نقض میشود؟
آها بله شرمنده اشتباه کردم
اما آیا “شکل دیگر رابطۀ تقسیم” هم اتحاد میشود؟
البته فکر میکنم بهتر میبود که سوالم را به شکل دیگری و زیر یک سوال دیگر مینوشتم که حتما برسی میکنم و اگر خودم به جواب نرسیدم، در زیر همان سوال میپرسم
ممنون بابت پاسخ سریع
نه. اون شکل دیگهش لزوماً اتحاد نمیشه.
لطفاً هر سؤالی که برات پیش میاد، بپرس. سؤال و جوابها اینجا میمونه و بقیه هم میخونن و یاد میگیرند؛ این خوبه.
خیلی ممنون
سلم وقتتون بخیر ببخشید چرا تمام چیز هایی که می خونیم مثلا مثال5برحسب یک متغیر هستند؟
سلام
چون در چنین مسائلی تفاوت خاصی وجود ندارد.
با یک متغیر را یاد بگیرید، کافی است.
سلام
لطفا در مورد کادر سبز رنگ دوم یا همان (شکل دیگر رابطه تقسیم )یک توضیح اضافی بدهید منظورشو نمیفهمم و هم رابطشو
ممنون
سلام
در رابطهٔ دوم کادر سبز دوم، دو طرف تساوی رابطهٔ اول بر \(P(x)\) تقسیم شده است:
\[\begin{aligned}&F(x)=P(x)\times Q(x)+R(x)\\[7pt]&\Rightarrow\frac{F(x)}{P(x)}=\frac{P(x)\times Q(x)}{P(x)}+\frac{R(x)}{P(x)}\\[7pt]&\Rightarrow\frac{F(x)}{P(x)}=Q(x)+\frac{R(x)}{P(x)}.\end{aligned}\]
من تو ماشین حساب بجای هرکدوم عدد میزارم ولی جواب درست نمیاد.
مثلا ۲۲ تقسیم بر ۳ که اگه بزاریمش تو فرمول بالا نتیجه میشه ۷.۳۳۳۳۳۳۳ = ۷.۶۶۶۶۶۶۶۶۶۶ البته دوره تناوب هم دارن …
اولاً، اشتباه شما این است که بهجای متغیرها عدد میگذارید! چندجملهایها برای خودشان شخصیت دارند! نباید بهجای متغیرهای آنها عدد بگذارید.
ثانیاً، اگر میخواهید چنین کاری انجام دهید، باید در رابطهٔ تقسیم بهجای متغیرها عدد بگذارید.
خیلی ممنون بخاطر تذکری که دادید.
فقط اینکه شما میدونید چرا وقتی ۲۲ تقسیم بر ۳ رو ( که میشه ۷.۳ ) میزاریم تو رابطه تقسیم جواب برابر ۲۲.۹ که همون ۲۳ هست میاد ؟ من هنگ کردم. 🙂
آیا قبول دارید که \(22.\overline{9}=23\)؟
نه ولی میدونیم که ۲۲ برابر ۲۲.۹ نیست
متوجه نمیشوم که رابطهٔ تقسیم شما چیست!
در تقسیم اعداد طبیعی، وقتی رابطه تقسیم مینویسید، همهٔ اعداد باید طبیعی باشند.
کجای رابطهٔ تقسیم شما عدد اعشاری وجود دارد؟
فهمیدم . باقی مانده تقسیم ۲۲ بر ۳ برابر یک دهم هست نه یک … ببخشید بخاطر اشتباه. لطفا اگه خواستید کامنت های بالا رو پاک کنید.
سلام… مثال 1 قسمت ب صورت عبارت با پاسخ همخوانی نداره
سلام. خیلی ممنون که تذکر دادید.
اصلاح شد.
مثال 2 هم به نظرم هر دو ایراد داره
از کجا معلوم p فقط ایکس 8 باشه؟
ممکنه ایکس 8 به علاوه ایکس 3 باشه!
درجه اش همچنان 8 می مونه
با عرض پوزش، در صورت مسئله، یک شرط جا افتاده بود.
با سپاس فراوان از شما که تذکر دادید. اصلاح شد.
توجه کنید که اگر مثلاً \(P(x)=x^8+3\) و \(Q(x)=x^2+12\)، بازهم درجهٔ حاصل تقسیم \(P(x)\) بر \(Q(x)\) برابر \(6\) است.
سلام
مثال 1 قسمت رو بررسی کنید گویا غلطی وجود داره
سلام
متأسفانه، متوجه نشدم که کدام قسمت مثال ۱ را میفرمایید.
با سلام , ممنون از مطالب مفیدتون , خیلی ساده و گیرا توضیح داده شده