۱. برای هریک از دنبالههای زیر، چهار جملهٔ اول و جملهٔ صدم را بیابید.
الف) $a_n=n^2-1$
\[\begin{aligned}a_1&=1^2-1=0\\a_2&=2^2-1=3\\a_3&=3^2-1=8\\a_4&=4^2-1=15\\a_{100}&=100^2-1=9999.\end{aligned}\]
ب) $c_n=\dfrac{(-1)^n}{n^2}$
\[\begin{aligned}c_1&=\frac{(-1)^1}{1^2}=\frac{-1}{1}=-1\\[6pt]c_2&=\frac{(-1)^2}{2^2}=\frac{1}{4}\\[6pt]c_3&=\frac{(-1)^3}{3^2}=\frac{-1}{9}\\[6pt]c_4&=\frac{(-1)^4}{4^2}=\frac{1}{16}\\[6pt]c_{100}&=\frac{(-1)^{100}}{100^2}=\frac{1}{10000}.\end{aligned}\]
ج) $t_n=(-1)^{n+1}\dfrac{n}{n+1}$
\[\begin{aligned}t_1&=(-1)^{1+1}\frac{1}{1+1}=(-1)^2\frac{1}{2}=\frac{1}{2}\\[8pt]t_2&=(-1)^{2+1}\frac{2}{2+1}=(-1)^3\frac{2}{3}=-\frac{2}{3}\\[8pt]t_3&=(-1)^{3+1}\frac{3}{3+1}=(-1)^4\frac{3}{4}=\frac{3}{4}\\[8pt]t_4&=(-1)^{4+1}\frac{4}{4+1}=(-1)^5\frac{4}{5}=-\frac{4}{5}\\[8pt]t_{100}&=(-1)^{100+1}\frac{100}{100+1}=(-1)^{101}\frac{100}{101}=-\frac{100}{101}.\end{aligned}\]
د) $s_n=1+(-1)^n$
\[\begin{aligned}s_1&=1+(-1)^1=1+(-1)=0\\s_2&=1+(-1)^2=1+1=2\\s_3&=1+(-1)^3=1+(-1)=0\\s_4&=1+(-1)^4=1+1=2\\s_{100}&=1+(-1)^{100}=1+1=2.\end{aligned}\]
هـ) $r_n=3$
\[\begin{aligned}r_1&=3\\r_2&=3\\r_3&=3\\r_4&=3\\r_{100}&=3.\end{aligned}\]
۲. جملهٔ عمومی هریک از دنبالههای زیر را بیابید.
الف) $2,4,8,16,\dots$
هریک از جملههای این دنباله توانهای طبیعی عدد $2$ هستند. پس جملهٔ عمومی این دنباله میتواند بهصورت زیر باشد.
\[a_n=2^n.\]
ب) $-\dfrac{1}{3},\dfrac{1}{9},-\dfrac{1}{27},\dfrac{1}{81},\dots$
هریک از جملههای این دنباله، بدون در نظر گرفتن علامت آنها، توانهای طبیعی عدد $\frac{1}{3}$ هستند. از طرفی، چون علامت جملهها یکیدرمیان عوض میشود، پس جملهٔ عمومی این دنباله را میتوان بهصورت زیر نوشت.
\[a_n=(-1)^n\frac{1}{3^n}.\]
ج) $3,0.3,0.03,0.003,\dots$
میتوان جملههای این دنباله را اینگونه نوشت:
\[\begin{aligned}a_{\color{red}1}&=3=\frac{3}{1}=\frac{3}{10^{\color{red}0}}\\[8pt]a_{\color{red}2}&=0.3=\frac{3}{10}=\frac{3}{10^{\color{red}1}}\\[8pt]a_{\color{red}3}&=0.03=\frac{3}{100}=\frac{3}{10^{\color{red}2}}\\[8pt]a_{\color{red}4}&=0.003=\frac{3}{1000}=\frac{3}{10^{\color{red}3}}.\end{aligned}\]
بنابراین، جملهٔ عمومی این دنباله میتواند بهصورت زیر باشد.
\[a_{\color{red}n}=\frac{3}{10^{\color{red}n-1}}.\]
د) $-2,3,8,13,\dots$
جملهٔ اول این دنباله، عدد $-2$ است؛ برای جملههای بعدی، هر جمله از جملهٔ قبلیاش $5$ واحد بیشتر است. یعنی اگر این دنباله را با حرف $a$ نامگذاری کنیم، آنوقت:
\[\begin{aligned}a_1&=-2\\a_2&=a_1+5=-2+5\\a_3&=a_2+5=(-2+5)+5=-2+2\times5\\a_4&=a_3+5=(-2+2\times5)+5=-2+3\times5.\end{aligned}\]
خاصیت مشترک بین این جملهها را میتوان بهصورت زیر نمایش داد.
\[\begin{aligned}a_{\color{red}1}&=-2+{\color{red}0}\times5\\a_{\color{red}2}&=-2+{\color{red}1}\times5\\a_{\color{red}3}&=-2+{\color{red}2}\times5\\a_{\color{red}4}&=-2+{\color{red}3}\times5.\end{aligned}\]
بنابراین، جملهٔ عمومی این دنباله میتواند بهصورت زیر باشد.
\[a_{\color{red}n}=-2+{\color{red}(n-1)}\times5.\]
هـ) $2,6,18,54,\dots$
جملهٔ اول این دنباله، عدد $2$ است؛ برای جملههای بعدی، هر جمله $3$ برابر جملهٔ قبلیاش است. یعنی اگر این دنباله را با حرف $a$ نامگذاری کنیم، آنوقت:
\[\begin{aligned}a_1&=2\\a_2&=a_1\times3=2\times3\\a_3&=a_2\times3=(2\times3)\times3=2\times3^2\\a_4&=a_3\times3=(2\times3^2)\times3=2\times3^3.\end{aligned}\]
خاصیت مشترک بین این جملهها را میتوان بهصورت زیر نمایش داد.
\[\begin{aligned}a_{\color{red}1}&=2\times3^{\color{red}0}\\a_{\color{red}2}&=2\times3^{\color{red}1}\\a_{\color{red}3}&=2\times3^{\color{red}2}\\a_{\color{red}4}&=2\times3^{\color{red}3}.\end{aligned}\]
بنابراین، جملهٔ عمومی این دنباله میتواند بهصورت زیر باشد.
\[a_{\color{red}n}=2\times3^{\color{red}n-1}.\]
و) $1,\dfrac{3}{4},\dfrac{5}{9},\dfrac{7}{16},\dfrac{9}{25},\dots$
صورت و مخرج اعضای این دنباله، بهترتیب اعداد فرد طبیعی و اعداد مربع کامل هستند:
\[\begin{aligned}\frac{1}{1},\frac{3}{4},\frac{5}{9},\frac{7}{16},\frac{9}{25},\dots.\end{aligned}\]
بنابراین، جملهٔ عمومی این دنباله میتواند بهصورت زیر باشد.
\[a_n=\frac{2n-1}{n^2}.\]
ز) $6,8,6,8,6,8,6,8,\dots$
اعداد این دنباله، یکیدرمیان، $1$ واحد از $7$ کمتر و $1$ واحد از $7$ بیشتر هستند. بنابراین، جملهٔ عمومی این دنباله میتواند بهصورت زیر باشد.
\[\begin{aligned}a_n=7+(-1)^n.\end{aligned}\]
ح) $1,\dfrac{1}{2},3,\dfrac{1}{4},5,\dfrac{1}{6},\dots$
در این دنباله، اعداد طبیعی یکیدرمیان معکوس شدهاند. بنابراین، جملهٔ عمومی این دنباله میتواند بهصورت زیر باشد.
\[a_n=n^{(-1)^{n+1}}.\]
۳. جملۀ عمومی یک دنباله بهصورت $a_n=\frac{3n-1}{n+2}$ است. جملۀ چندم این دنباله برابر $\frac{20}{9}$ میشود؟
باید $n$ای را پیدا کنیم که بهازای آن حاصل $\frac{3n-1}{n+2}$ برابر $\frac{20}{9}$ شود. یعنی:
\[\begin{aligned}&\frac{3n-1}{n+2}=\frac{20}{9}\\[6pt]&\Rightarrow 9(3n-1)=20(n+2)\\&\Rightarrow 27n-9=20n+40\\&\Rightarrow 7n=49\\&\Rightarrow n=7.\end{aligned}\]
۴. در یک کشور، میانگین قیمت یک کالا هر سال $6$ درصد افزایش یافته است. در سال $2002$ میانگین قیمت این کالا $240\,000$ دلار بوده است. فرض کنید $a_n$ نشاندهندهٔ میانگین قیمت این کالا برای $n$ سال پس از سال $2002$ باشد.
الف) فرمول دنبالهٔ $a_n$ را بیابید.
میانگین قیمت این کالا در سال $2003$:
\[a_1=1.06\times240\,000.\]
میانگین قیمت این کالا در سال $2004$:
\[\begin{aligned}a_2&=(1.06)a_1\\&=(1.06)(1.06\times240\,000)\\&=(1.06)^2\times240\,000.\end{aligned}\]
میانگین قیمت این کالا در سال $2005$:
\[\begin{aligned}a_3&=(1.06)a_2\\&=(1.06)\big((1.06)^2\times240\,000\big)\\&=(1.06)^3\times240\,000.\end{aligned}\]
بنابراین، میانگین قیمت این کالا $n$ سال بعد از سال $2002$ از رابطهٔ زیر بهدست میآید:
\[a_n=(1.06)^n\times240\,000.\]
ب) میانگین قیمت این کالا در سال $2010$ چقدر بوده است؟
\[a_{2010-2002}=a_{8}=(1.06)^8\times240\,000=382523.538\]
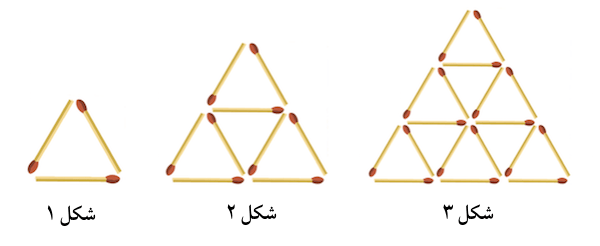
۵. در هریک از الگوهای چوبکبریتی زیر، تعداد چوبکبریتها یک دنباله میسازند. جملۀ عمومی هر دنباله را بیابید.
الف) 
شکل ۱ را یک مثلث سربالا مینامیم. میخواهیم تعداد مثلثهای سربالا در شکل \(n\)اُم را بشماریم.
در سطر اول (از بالا) شکل $n$اُم، $1$ مثلث سربالا وجود دارد.
در سطر دوم شکل $n$اُم، $2$ مثلث سربالا وجود دارد.
در سطر سوم شکل $n$اُم، $3$ مثلث سربالا وجود دارد.
$\quad$ $\vdots$
در سطر $n$اُم شکل $n$اُم، $n$ مثلث سربالا وجود دارد.
بنابراین تعداد مثلثهای سربالا در شکل $n$اُم برابر است با:
\[1+2+3+\dots+n.\]
بنابراین، تعداد مثلثهای سربالا در شکل $n$اُم برابر است با:
\[\begin{aligned}1+2+3+\dots+n=\frac{n(n+1)}{2}.\end{aligned}\]
چون تعداد چوبکبریتهای شکل $n$اُم با مجموع چوبکبریتهایی که مثلثهای سربالا را میسازند برابر است، پس تعداد چوبکبریتهای شکل $n$اُم برابر است با:
\[3\times\frac{n(n+1)}{2}.\]
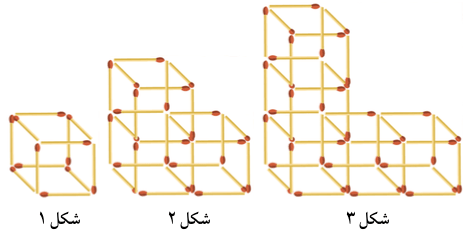
ب)

شکل ۱، \(12\) چوبکبریت دارد.
تعداد چوبکبریتهای شکل ۲ را میتوان اینگونه شمرد؛ یک مکعب با \(12\) چوبکبریت و \(2\) مکعب با \(8\) چوبکبریت:\[12+2(8).\]
تعداد چوبکبریتهای شکل ۳ را میتوان اینگونه شمرد؛ یک مکعب با \(12\) چوبکبریت و \(4\) مکعب با \(8\) چوبکبریت: \[12+4(8).\]
تعداد چوبکبریتهای شکل ۴ را میتوان اینگونه شمرد؛ یک مکعب با \(12\) چوبکبریت و \(6\) مکعب با \(8\) چوبکبریت: \[12+6(8).\]
بنابراین، تعداد چوبکبریتهای شکل \(n\) را میتوان اینگونه شمرد؛ یک مکعب با \(12\) چوبکبریت و \(2n-2\) مکعب با \(8\) چوبکبریت: \[12+(2n-2)(8).\]
پرسش. آیا میتوانید حداقل دو روش دیگر برای حل این مسئله ارائه کنید؟
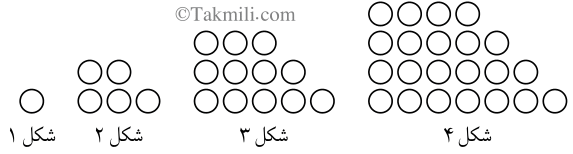
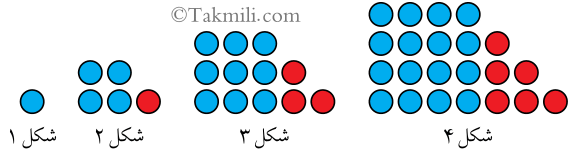
۶. شکل نهم الگوی زیر، چند دایره دارد؟

تعداد دایرههای شکلهای اول تا چهارم، بهترتیب برابرند با:
\[\begin{aligned}&{\color{blue}1\times1},\\&{\color{blue}2\times2}+{\color{red}1},\\&{\color{blue}3\times3}+{\color{red}1+2},\\&{\color{blue}4\times4}+{\color{red}1+2+3}.\end{aligned}\]

بنابراین، تعداد دایرههای شکل نهم برابر است با:
\[\begin{aligned}&{\color{blue}9\times9}+{\color{red}1+2+3+\dots+8}\\&={\color{blue}81}+{\color{red}\frac{8\times9}{2}}\\&={\color{blue}81}+{\color{red}36}\\&=117.\end{aligned}\]
۷. سه جملهٔ اول یک دنباله را داریم:
\[1,4,9,\dots.\]
برای این دنباله، دو جملهٔ عمومی متفاوت پیدا کنید و در هریک، سه جملهٔ بعدی را بنویسید.
جملهٔ عمومی اول:
\[a_n=n^2.\]
در این حالت، شش جملهٔ اول دنباله عبارتند از:
\[1,4,9,16,25,36,\dots.\]
جملهٔ عمومی دوم:
\[b_n=n^2+(n-1)(n-2)(n-3).\]
در این حالت، شش جملهٔ اول دنباله عبارتند از:
\[1,4,9,22,49,96,\dots.\]
سؤال. آیا میتوانید جملهٔ عمومی دیگری برای این دنباله بیابید؟
۸. چهار جملهٔ اول یک دنباله را داریم:
\[2,4,8,16,\dots.\]
برای این دنباله، دو جملهٔ عمومی متفاوت پیدا کنید و در هریک، سه جملهٔ بعدی را بنویسید.
جملهٔ عمومی اول:
\[a_n=2^n.\]
در این حالت، هفت جملهٔ اول دنباله عبارتند از:
\[2^1,2^2,2^3,2^4,2^5,2^6,2^7,\dots.\]
جملهٔ عمومی دوم:
\[b_n=2^{n+(n-1)(n-2)(n-3)(n-4)}.\]
در این حالت، هفت جملهٔ اول دنباله عبارتند از:
\[2^1,2^2,2^3,2^4,2^{29},2^{126},2^{367},\dots.\]
۹. دنبالهٔ زیر را در نظر بگیرید. \[-2,0,2,4,\dots\] اگر جملهٔ عمومی این دنباله را با \(a_n\) نمایش دهیم، آیا میتوان \(a_n\) را طوری تعیین کرد که
الف) \(a_5=6\)؟
ب) \(a_5=111\)؟
\[a_n=2(n-2)+(n-1)(n-2)(n-3)(n-4)\times\frac{35}{8}.\]
ج) \(a_5=7\)؟
\[a_n=2(n-2)+(n-1)(n-2)(n-3)(n-4)\times\frac{1}{24}.\]



ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️سلام وقت بهخیر
در سؤال ۸، آیا جملهٔ عمومی نمیتواند عبارت زیر باشد؟\[b_n=2^n+(n-1)(n-2)(n-3)(n-4)\]
سلام
بله. این هم مثال بسیار خوبی است.