درسنامهٔ اتحاد و تجزیه – جلسهٔ هشتم – روش Horner

برای اینکه درسنامه‌های سایت تکمیلی به‌خوبی بیاموزید، حتماً روی لینک زیر کلیک کنید و از روش ارائه شده در آن استفاده کنید.

چگونه درسنامه‌های سایت تکمیلی را بخوانیم؟

روش هورنر

برای دانلود ویدئوی بالا، اینجا را کلیک کنید.

مثال ۱. با روش هورنر، خارج‌قسمت و باقی‌ماندهٔ هریک از تقسیم‌های زیر را محاسبه کنید.

الف) \(2x^3+14x^2-20x+7\) تقسیم بر \(x+6\)

ابتدا ریشهٔ مقسوم‌علیه را پیدا می‌کنیم:
\[x+6=0\Longrightarrow x=-6.\]
سپس، با استفاده از روش هورنر داریم:

ب) \(x^4-10x^2-2x+4\) تقسیم بر \(x+3\)

توجه کنید که در چندجمله‌ای \(x^4-10x^2-2x+4\)، ضریب جملهٔ \(x^3\) برابر \(0\) است. پس بنابه روش هورنر داریم:

پس خارج‌قسمت و باقی‌مانده به‌ترتیب \(x^3-3x^2-x+1\) و \(1\) هستند.

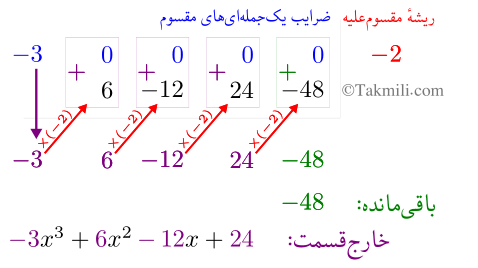
ج) \(-3x^4\) تقسیم بر \(x+2\)

توجه کنید که در چندجمله‌ای \(-3x^4\) ضریب جمله‌های درجه \(3\)، درجه \(2\)، درجه \(1\)، و درجه \(0\) برابر \(0\) است. پس بنابه روش هورنر داریم:

د) \(9x^3-16x-18x^2+32\) تقسیم بر \(x-2\)

ابتدا مقسوم را استاندارد می‌کنیم:
\[\begin{aligned}&9x^3-16x-18x^2+32\\&=9x^3-18x^2-16x+32.\end{aligned}\]
سپس، با استفاده از روش هورنر داریم:

پس خارج‌قسمت و باقی‌مانده به‌ترتیب \(9x^2-16\) و \(0\) هستند.
پرسش. حالا باید بتوانید همهٔ ریشه‌های چندجمله‌ای \(9x^3-16x-18x^2+32\) را بیابید. چگونه این کار را انجام می‌دهید.

هـ) \(5-3x+2x^2-x^3\) تقسیم بر \(x+1\)

ابتدا مقسوم را استاندارد می‌کنیم:
\[\begin{aligned}&5-3x+2x^2-x^3\\&=-x^3+2x^2-3x+5.\end{aligned}\]
سپس، با استفاده از روش هورنر داریم:

پس خارج‌قسمت و باقی‌مانده به‌ترتیب \(-x^2+3x-6\) و \(11\) هستند.

مثال ۲. به‌ازای چند عدد صحیح مثل \(n\)، عبارت \(\dfrac{2n^2+9n+13}{n+2}\) عددی صحیح است؟

با استفاده از روش هورنر، خارج قسمت و باقی‌ماندهٔ تقسیم \(2n^2+9n+13\) را بر \(n+2\) محاسبه می‌کنیم.

در نتیجه، داریم:
\[\begin{aligned}\frac{2n^2+9n+13}{n+2}=2n+5+\frac{3}{n+2}\cdot\end{aligned}\]
پس \(n+2\) باید یکی از عددهای \(-3\)، \(-1\)، \(1\)، یا \(3\) باشد؛ بنابراین، \(n\) باید یکی از عددهای \(-5\)، \(-3\)، \(-1\)، یا \(1\) باشد.

زنگ تفریح

تمرین‌های روش هورنر

برای اینکه به این روش تقسیم سریع چندجمله‌ای‌ها مسلط‌تر شوید، حتماً تمرین‌های این بخش را حل کنید.

تمرین‌های روش هورنر

فهرست درسنامهٔ اتحاد و تجزیه

با کلیک روی هریک از لینک‌های زیر، صفحهٔ مربوطه باز خواهد شد.جلسهٔ اول: تعریف اتحادتمرین‌های جلسهٔ اول
جلسهٔ دوم: یک‌جمله‌ای‌هاتمرین‌های جلسهٔ دوم
جلسهٔ سوم: چندجمله‌ای‌هاتمرین‌های جلسهٔ سوم
جلسهٔ چهارم: درجهٔ چندجمله‌ای‌هاتمرین‌های جلسهٔ چهارم
جلسهٔ پنجم: ریشهتمرین‌های جلسهٔ پنجم
جلسهٔ ششم: تقسیم چندجمله‌ای‌هاتمرین‌های جلسهٔ ششم
جلسهٔ هفتم: ریشهٔ مقسوم‌علیه و محاسبهٔ باقی‌ماندهتمرین‌های جلسهٔ هفتم
جلسهٔ هشتم: روش هورنرتمرین‌های جلسهٔ هشتم
جلسهٔ نهم: بخش‌پذیری در چندجمله‌ای‌هاتمرین‌های جلسهٔ نهم
جلسهٔ‌ دهم: تعریف تجزیهتمرین‌های جلسهٔ دهم
جلسهٔ یازدهم: رفتار چندجمله‌ای‌هاتمرین‌های جلسهٔ یازدهم
جلسهٔ دوازدهم: فاکتورگیریتمرین‌های جلسهٔ دوازدهم
جلسهٔ سیزدهم: اتحاد مربع دوجمله‌ایتمرین‌های جلسهٔ سیزدهم
جلسهٔ چهاردهم: اتحاد مزدوجتمرین‌های جلسهٔ چهاردهم
جلسهٔ پانزدهم: اتحاد جمله مشترکتمرین‌های جلسهٔ پانزدهم
جلسهٔ شانزدهم: مربع‌سازیتمرین‌های جلسهٔ شانزدهم
جلسهٔ هفدهم: یافتن ریشهٔ چندجمله‌ای درجه ۲تمرین‌های جلسهٔ هفدهم
جلسهٔ هجدهم: تجزیهٔ یک چندجمله‌ای درجه ۴تمرین‌های جلسهٔ هجدهم
جلسهٔ نوزدهم: مجموع مربعاتتمرین‌های جلسهٔ نوزدهم
جلسهٔ بیستم: اتحاد چاق و لاغرتمرین‌های جلسهٔ بیستم
جلسهٔ بیست‌ویکم: چند اتحاد دیگرتمرین‌های جلسهٔ بیست‌و‌یکم
جلسهٔ بیست‌ودوم: تکنیک‌های سنتی تجزیهتمرین‌های جلسهٔ بیست‌و‌دوم