نهم. فصل ۳. قضیهٔ زاویهٔ محاطی

قضیهٔ زاویهٔ محاطی. اندازهٔ هر زاویهٔ محاطی با نصف کمان روبه‌رو به ‌آن زاویه برابر است.

---

فرض. زاویه‌ای، مانند زاویهٔ \(ABC\)، یک زاویهٔ محاطی در یک دایره است.

حکم. اندازهٔ زاویهٔ \(ABC\)، نصف اندازهٔ کمان \(AC\) است.

---

اثبات. فرض کنیم نقطهٔ \(O\) مرکز دایره باشد. سه‌حالت برای زاویهٔ \(ABC\) در نظر می‌گیریم:
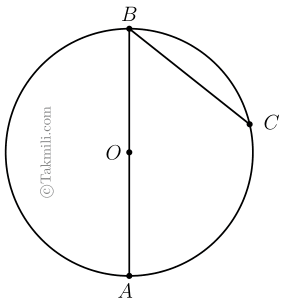
حالت اول. نقطهٔ‌ \(O\) روی یکی از ضلع‌های زاویهٔ \(ABC\) باشد.

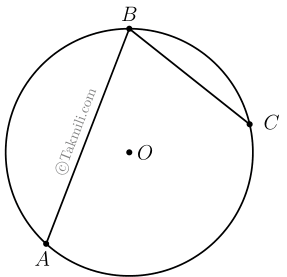
حالت دوم. نقطهٔ‌ \(O\) درون زاویهٔ \(ABC\) باشد.

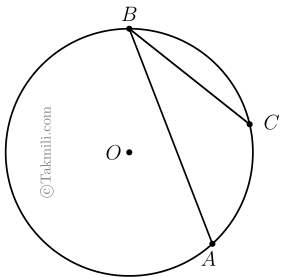
حالت سوم. نقطهٔ‌ \(O\) بیرون زاویهٔ \(ABC\) باشد.

اثبات حالت اول. فرض کنیم \(O\) روی \(AB\) باشد. برای سادگی، اندازهٔ زاویهٔ \(ABC\) را با \(x\) نشان می‌دهیم.

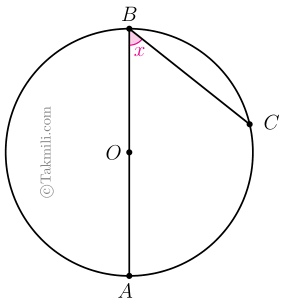
از \(O\) به \(C\) وصل می‌کنیم. در این‌صورت \(OB=OC\). (چرا؟)

پس بنابه قضیهٔ مثلث متساوی‌الساقین، داریم: \[O\widehat{B}C=O\widehat{C}B=x.\quad(1)\]

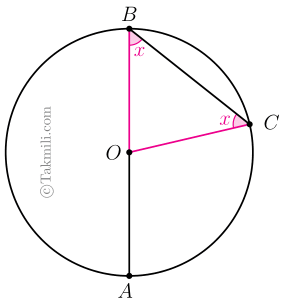
از رابطهٔ \((1)\) و قضیهٔ زاویهٔ خارجی مثلث نتیجه می‌شود که \(A\widehat{O}C=2x\). چون زاویهٔ \(AOC\) زاویهٔ مرکزی است، پس اندازهٔ کمان \(AC\) نیز برابر \(2x\) است.

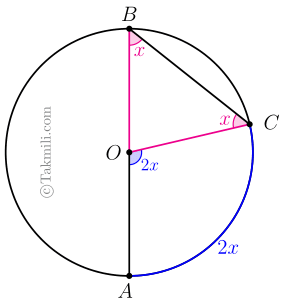بنابراین، زاویهٔ محاطی \(ABC\) نصف کمان روبه‌رویش است.

اثبات حالت دوم. پاره‌خطی از \(B\) به \(O\) وصل می‌کنیم و آن را امتداد می‌دهیم تا دایره را در نقطهٔ‌ \(D\) قطع کند. برای سادگی قرار می‌دهیم \(A\widehat{B}D=y\) و \(C\widehat{B}D=z\).

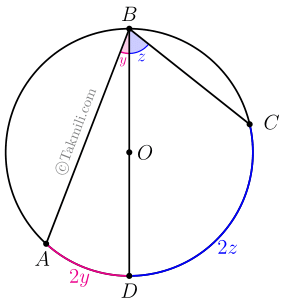
در این‌صورت، اندازهٔ کمان‌های \(AD\) و \(BC\) به‌ترتیب برابر \(2y\) و \(2z\) است. (چرا؟)

پس:
\[\left.\begin{aligned}&A\widehat{B}C=y+z\\&\overset{\frown}{AC}=2y+2z\end{aligned}\right\}\Rightarrow A\widehat{B}C=\frac{1}{2}\overset{\frown}{AC}.\]

اثبات حالت سوم. پاره‌خطی از \(B\) به \(O\) وصل می‌کنیم و آن را امتداد می‌دهیم تا دایره را در نقطهٔ \(D\) قطع کند. برای سادگی قرار می‌دهیم \(A\widehat{B}C=w\) و \(A\widehat{B}D=t\).

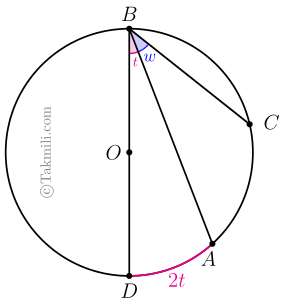
در این‌صورت، اندازهٔ کمان‌های \(CAD\) و \(AD\) به‌ترتیب برابر \(2w+2t\) و \(2t\) است. (چرا؟)

در نتیجه: \[\begin{aligned}\overset{\frown}{AC}&=\overset{\frown}{CAD}-\overset{\frown}{AD}\\&=2(w+t)-2t\\&=2w+2t-2t\\&=2w.\end{aligned}\]

پس اندازهٔ زاویهٔ \(ABC\) نصف کمان روبه‌رویش است.