قضیهٔ عمودمنصّف. هر نقطه روی عمودمنصّفِ یک پارهخط از دو سر آن پارهخط فاصلهٔ یکسان دارد.
عکس قضیهٔ عمودمنصّف. اگر نقطهای از دو سر یک پارهخط فاصلهٔ یکسان داشته باشد، این نقطه روی عمودمنصّف پارهخط قرار دارد.
فرض. نقطهای مانند \(M\) روی عمودمنصف پارهخطی، مانند \(AB\)، قرار دارد.
حکم. \(MA=MB\).
اثبات قضیهٔ عمود منصف. فرض کنیم خط $d$ عمودمنصف پارهخط $AB$ باشد و آن را در نقطهٔ $H$ قطع کرده باشد. نقطهٔ دلخواه $M$ را روی خط $d$ انتخاب میکنیم.

دو مثلث $AMH$ و $BMH$ در حالت ضزض همنهشتاند.(چرا؟)
اکنون، از همنهشتی دو مثلث \(AMH\) و \(BMH\) نتیجه میشود که $AM=BM$.
اثبات عکس قضیهٔ عمودمنصف. فرض کنیم فاصلهٔ نقطهٔ $M$ از دو سر پارهخط $AB$ یکسان باشد؛ یعنی $AM=BM$.
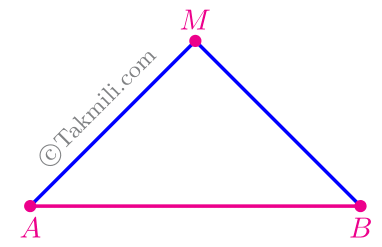
میخواهیم ثابت کنیم که نقطهٔ \(M\) روی عمودمنصف \(AB\) قرار دارد.
میانهٔ $MN$ از مثلث $AMB$ را رسم میکنیم. پس \(AN=BN\). حال کافی است ثابت کنیم که \(MN\) بر \(AB\) عمود است.
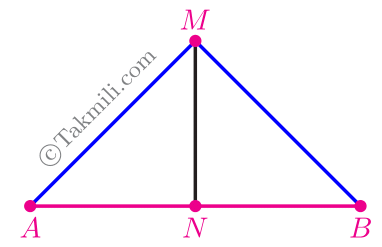
دو مثلث $AMN$ و $BMN$ در حالت ضضض همنهشتاند. (چرا؟)
از همنهشتی دو مثلث \(AMN\) و \(BMN\) نتیجه میشود: \[A\widehat{N}M=B\widehat{N}M=90^\circ.\] پس \(MN\) هم \(AB\) را نصف میکند و هم بر آن عمود است. بنابراین، نقطهٔ \(M\) روی عمودمنصف \(AB\) قرار دارد.

ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️سلام خسته نباشید
درست متوجه شدم که حکم رو به این شکل ساده سازی کردید که AN=NB و N1=N2=90
اما خب در اثبات هم نهشتی دارید از همون میانه بودن یا همون AN=NB استفاده میکنید خب این دور باطل نیست که دارید برای اثبات حکم از بخشی از حکم استفاده میکنید؟
خیلی ممنون از پاسخگویی تون
سلام
نه. این استدلال ربطی به دور باطل ندارد. ما میانه را رسم میکنیم و اثبات میکنیم که میانه روی عمودمنصف است.
در حالت عکس چطوری میگید میانه عمود هم هست
فقط با میانه تونستید دو مثلث رو اثبات کنید
چطور نتیجه گیری میکنید که N=90 است
چون ثابت کردیم دو زاویهٔ \(ANM\) و \(BNM\) برابرند، نتیجه میشود هر کدام \(90\) درجه هستند. زیرا \(A\)، \(N\)، و \(B\) روی یک خط قرار دارند.
در حالت عکس چطور نتیجه گرفتید که میانه عمود هم هست
فقط تونستیم اثبات کنیم دو مثلث هم نهشت اند
دلیلی برای عمود بودن میانه ذکر نشده
وقتی ثابت کردیم دو زاویهٔ \(ANM\) و \(BNM\) برابرند، نتیجه میشود هر کدام \(90\) درجه هستند. چود \(A\)، \(N\)، و \(B\) روی یک خط قرار دارند.
سلام خسته نباشید
اساتید ما گفتن که نمیشه از میانه استفاده کرد چون در حالت دور(باطل) قرار میگیره و اثبات نادرست میشه
سلام
اساتید گفتن در هر مسئلهای که از میانه استفاده کنید در «حالت دور(باطل) قرار میگیره»؟ یا در این مسئله؟
در این مسئله دور باطل وجود ندارد و استدلال دقیق و کامل است. اگر دور باطلی میبینید، دقیقتر آن را مشخص کنید.
مي شد به جاي ميانه نيمساز رسم کنيم
طبیعتاً در مسئلههای هندسه راهحل متفاوتی وجود دارد که در این سایت ما همهٔ راهحلهای ممکن را نمینویسیم.
اما اینکه چرا در اینجا بهجای نیمساز، از میانه استفاده کردهایم، یک دلیل فنی دارد: «قضیهٔ قطعهبُر»! (اگر علاقهمند هستید میتوانید این قضیه را در کتاب هندسههای اقلیدسی و نااقلیدسی و بسط آنها بخوانید.
آزمون نوبت دوم مدارس تیزهوشان
میشه نمونه سوال آزمون نوبت دوم ریاضی رو برامون قرار بدید
فقط تا 7 خرداد قرار بدید ممنون
از صفحهٔ اصلی سایت وارد پایه مورد نظرتان شوید و نمونه سؤالات را مشاهده کنید.
خیلییی خوب بود کارم راه افتاد
میشه یه کار دیگه هم کرد:
به جای رسم میانه، یک خط عمود بر AB رسم کنیم بعد با همنهشتی اثبات کنیم که AN=NB
رسم خط عمود ایراد داره! از کجا میدانید که عمودی که رسم میکنید، داخل مثلث میافته؟
چرا نیوفته؟
کسی که ادعا میکنه عمود داخل میافته باید دلیل آن را هم بنویسد. اگر بهطور دقیق و ریاضیاتی، اثبات کردید که عمود داخل مثلث میافته، اثبات شما کامل است.
چرا نیوفته؟
مثلث ما متساوی الساقین هستش
داریم میگیم از دوسر پاره خط به یک اندازه است
فقط در یک حالت خط عمود داخل مثلث نمیوفته که اونم مثلث منفرجه است که قبل تر گفتیم نیست
پس با خط عمود هم میتونیم اثبات کنیم
بسیار عالی
سلام
برای عکس قضیه در واقع ما فرض کردیم که خط میانه رو پیدا کردیم و بعد اون رو رسم کردیم ( می دونیم که قطعا از راس رسم میشه ) بعد اثبات هم نهشتی بود و بعد مشخص شد که روی خط عمود هم هست در واقع واضح بود که میانه مثلث ازش میگذره اما اینکه ایا همین میانه عمود نیز هست مسئله ای بود که به دنبال اثبات کردنش بودیم. درسته؟
سلام
بله! اگر میانه، عمود هم باشد، آنگاه میانه و عمومنصف برهم منطبقاند.
به نظرم کمی غیر واقعی هست بهتر بود یک جدول زمانی تهیه می کردین هم کار باید وهم درآمد زا وان لاین
ببخشید. متوجه نشدم! جدول زمانی برای چه کاری تهیه میکردیم؟
ایا فقط مثلث متساوی الساقین هست که از یک راس آن میشه بر ضلع مقابلش عمود منصف رسم کرد(یعنی مثلث های دیگر این قابلیت را ندارند؟)
در اینجا، همین مطلبی که شما نوشتهاید ثابت شده است.
فقط توجه کنید که عمودمنصف را از رأس نمیکشند! عمودمنصف خطی است که از وسط یک پارهخط میگذرد و بر آن عمود است.
بله درسته پس در مثلث متساوی الساقین یکی از عمود منصف هایی که رسم میکنیم از راس مقابلش میگذره.ممنون??
سلام برای اثبات قضیه عمود منصف،بایدقضیه عکس روهم بنویسیم؟
سلام
خیر! برای اثبات قضیهٔ عمودمنصف نیازی به نوشتن عکس آن نیست.
در این صفحه، هم قضیهٔ عمودمنصف اثبات شده است و هم عکس آن.
سلام ببخشید من در این مسئله مشکل پیدا کردم ما در اثبات عکس عمود منصف ، منصف بودش رو اثبات نمی کنیم بلکه از اون در فرض استفاده می کنیم و در واقع فقط عمود بودنش رو ثابت می کنینم میشه یه توضیح بدید لطفا؟
سلام
در اثبات عکس قضیه عمود منصف، ابتدا میانه را رسم میکنیم و سپس ثابت میکنیم که این میانه بر پارهخط داده شده عمود هم هست؛ درواقع، ثابت میکنم که میانه، عمودمنصف مثلث است. و اینکار برای اثبات کافی است.
سلام خسته نباشید.می تونیم برای اثبات عکس قضیه عمود منصف به جای رسم میانه نیمساز رو رسم کنیم و از رابطه _____ (ز ض ز ) هم نهشتی را اثبات کنیم؟؟؟
سلام. میشه نیمساز رو رسم کرد ولی باید از حالت همنهشتی ضزض استفاده کرد.
اما وقتی نیمساز رو رسم میکنیم باید از یه قضیهٔ دیگه هم استفاده کنیم!! در هندسهٔ خیلی دقیق، یکی از مسائل این است که چرا نیمساز مثلث، ضلع مقابل را قطع میکند!! (شاید باورتون نشه…) تو کتابهای هندسهٔ پیشرفته، قضیهای هست بهنام «قضیهٔ قطعهبر» که دربارهٔ چنین مسئلهای حرف میزند. اگر علاقه داشتید، اصول، تعاریف، و قضیههای هندسه را خیلی دقیق بیاموزید، خواندن کتاب هندسههای اقلیدسی و نااقلیدسی را به شما پیشنهاد میکنم. البته، این کتاب برای حل مسئلههای هندسهٔ دبیرستانی نیست و اگر صرفاً میخواهید در هندسهٔ دبیرستانی و حل مسائل پیچیده پیشرفت کنید، خواندن این کتاب را توصیه نمیکنم!