قضیه نیمساز. هر نقطه روی نیمساز یک زاویه از دو ضلع آن زاویه فاصلهٔ یکسان دارد.
عکس قضیه نیمساز. اگر نقطهای از دو ضلع یک زاویه فاصلهٔ یکسان داشته باشد، این نقطه روی نیمساز آن زاویه قرار دارد.
فرض. نقطهای مانند \(D\) روی نیمساز زاویهای مانند \(A\) قرار دارد.
حکم. فاصلهٔ نقطهٔ \(D\) از دو ضلع زاویهٔ \(A\) یکسان است.
در عکس قضیه، جای فرض و حکم عوض میشود.
اثبات قضیهٔ نیمساز. نقطهٔ دلخواه $D$ را روی نیمساز زاویهٔ ${A}$ انتخاب میکنیم. از $D$ دو عمود $DH$ و $DK$ را بر ضلعهای زاویهٔ $A$ رسم میکنیم. باید ثابت کنیم که \(DH=DK\).
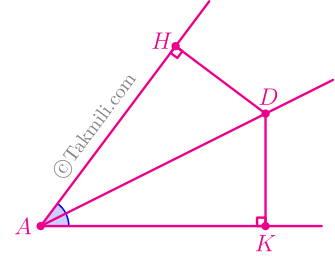
دو مثلث $AHD$ و $AKD$ در حالت ززض همنهشتاند. (چرا؟)
از همنهشتی دو مثلث \(AHD\) و \(AKD\) نتیجه میشود که $DH=DK$.
اثبات عکس قضیهٔ نیمساز. نقطهٔ $M$ از دو ضلع زاویهٔ $A$ فاصلهٔ یکسان دارد؛ یعنی اگر دو عمود $MH$ و $MK$ را بر ضلعهای زاویهٔ $A$ وارد کنیم، آنگاه $MH=MK$. باید ثابت کنیم که \(AM\) نیمساز زاویهٔ \(HAK\) است.
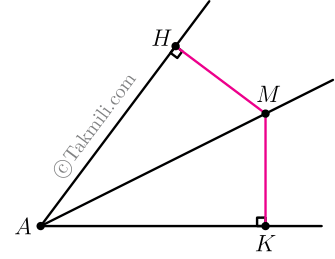
دو مثلث $AMH$ و $AMK$ در حالت وتر و یکضلع همنهشتاند. (چرا؟)
از همنهشتی دو مثلث \(AMH\) و \(AMK\) نتیجه میشود که \(H\widehat{A}M=K\widehat{A}M\). پس $AM$ نیمساز زاویهٔ $A$ است.



ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️ززض نیست وز هست
وتر و یک ضلع مسخرهترین چیزی است که در کتابهای درسی نوشته شده است.
برای مشاهدهٔ دلیل، حتماً اینجا را کلیک کنید.
سلام.خسته نباشید.ببخشید برای بخش اول که از طریق ززض هم نهشتی دو مثلث را اثبات کردید نمیشد از وز اثبات کنیم؟(وتر مشترک هست و دو زاویه برابر هم دارد)
سلام
حالت وز، حالت خاص ززض است. «وتر و یک زاویهٔ تند» مسخرهترین قضیه در کتابهای درسی است! حتماً اینجا را کلیک کنید و دلیل مسخره بودن وز را بخوانید.
لطفا جواب این جای خالی را بگید
نیمساز های دو مثلث هم نهشت نظیر به نظیر ….. است
یعنی چه؟ منظورتان این است که «برابر» هستند یا نه؟
این سؤال شما، یک مسئلهٔ ریاضی است!؟؟
اگر برابر باشند باید حتماً اثبات بنویسید و درغیر اینصورت مثال نقض بیاورید.
سایت تکمیلی جای مناسبی برای اینگونه پرسشها نیست. در سایت تکمیلی، بحثهای ریاضیاتی بهصورت کاملاً حرفهای و دقیق بررسی میشوند؛ نه مثل کتابهای تستی و بازاری!
برای اثبات : هر نقطه روی نیمساز از دو ضلع زاویه به یک اندازه است از کدام حالت هم نهشتی مثلث استفاده می کنیم؟
و ض
و ز
ز ض ز
ض ز ض
آیا سؤال شما یک پرسش چهارگزینهای است که فقط یک گزینه باید درست باشد؟
اگر اینطور است، هم وز درست است و هم زضز؛ و بنابراین، پرسش چهارگزینهای شما غلط است!
البته، بارها گفتهایم که «وز» یکی از مسخرهترین حالتهای همنهشتی مثلثهاست! برای خواندن توضیحات مفصل در اینباره، اینجا را کلیک کنید.
قضیه ی نیم ساز بر اساس وتر و یک زاویه ی تند هم میشه که بهتره تا ززض
اگر واقعاً میدانستید که «وتر و یک زاویهٔ تند» چقدر مسخره است، هرگز چنین چیزی نمینوشتید!
ما میدانیم که همهٔ مثلثها در حالت ززض همنهشتاند. حالت وتر و یک زاویهٔ تند، در واقع همان حالت ززض در مثلث قائمالزاویه است (برابری وترها، یک زاویهٔ تند، و یک زاویهٔ قائمه). چرا باید در مثلث قائمالزاویه برای حالت ززض، اسم دیگری بگذاریم؟!
اعصاب ندارید هااا
🙂
با سلام? ممنونم از ازاطلاعات خوبتون❤
یه سوال داشتم?
اگر نقطه ای روی نیمساز یک زاویه قرار داشته باشه بهش چی میگن؟ چه اتفاقی میوفته؟؟
سلام
چنین نقطهای اسم خاصی نداره. حداقل اسمش جهانی نیست.
سلام ببخشید یک سوال ما اصلا حالت ز ز ض نداریم !!! شما در بالا نوشتین
سلام
حالت ززض دارید!!! و در صفحهٔ ۴۸ کتاب ریاضیات تکمیلی نهم نیز آمده است.
ببخشید من هشتم هستم و معلممان امروز داشت این قضیه را اثبات میکرد گفت اصلا چنین حالتی نداریم ….الان من برم به ایشون بگم در تکمیلی نهم آمده؟ ببخشید امکان داره بگین در کدام فصلش؟یعنی فصل چند؟
این قضیه در تمرین ۱۱ صفحهٔ ۹۸ کتاب ریاضیات تکمیلی هشتم نیز شرح داده شده است. اگر کتاب ریاضیات تکمیلی نهم را دانلود کنید، میتوانید در صفحهٔ ۴۸ از فصل ۳ این کتاب، قضیهٔ ززض را ببینید.
احتمالاً معلم شما از حالت وتر و یک زاویهٔ حاده استفاده کرده است. به شکلهای زیر، دقت کنید.
در مثلثهای قائمالزاویهٔ بالا، \(BC=EF\) و \(\widehat{B}=\widehat{E}\). احتمالاً معلم شما میگوید که دو مثلث بالا در حالت وتر و یک زاویهٔ حاده همنهشتاند. اما وتر و یک زاویهٔ حاده، یک حالت خاص از قضیهٔ ززض است.
با استفاده از حالت ززض در مثلثهای بالا، دو زاویهٔ برابر، عبارتند از:
\[\begin{aligned}\widehat{B}&=\widehat{E}\\\widehat{A}&=\widehat{D}=90^\circ.\end{aligned}\] و یکی از ضلعهای غیر بین این دو زاویه نیز نظیر به نظیر برابرند:
\[BC=EF.\]
اثبات قضیهٔ ززض با استفاده از قضیهٔ مجموع زاویههای مثلث، بسیار ساده است: «چون دو زاویه از یک مثلث با دو زاویه از مثلث دیگر برابر است، و میدانیم مجموع زاویههای هر مثلث برابر \(180\) درجه است، پس زاویهٔ سوم این دو مثلث نیز برابرند. در نتیجه، حالت ززض تبدیل به حالت زضز میشود.»
در مثال بالا، و با استفاده از قضیهٔ مجموع زاویههای مثلث، واضح است که زاویههای \(C\) و \(F\) نیز برابرند و دو مثلث داده شده در حالت زضز همنهشتاند.
در واقع، حالت ززض برای همهٔ مثلثها درست است؛ اما کتابهای درسی از این حالت فقط در مثلثهای قائمالزاویه استفاده میکنند!!!
البته، توجه داشته باشید که برای استفاده از حالت ززض، نظیربهنظیر بودن ضلعهای برابر بسیار مهم است. تمرین ۱۱ صفحهٔ ۹۸ کتاب ریاضیات تکمیلی هشتم این نکتهٔ مهم را بهخوبی آموزش میدهد.
همانطور که دیدید، اثبات قضیهٔ ززض بسیار آسان بود! و بهراحتی از قضیهٔ زضز نتیجه شد. حال، سؤالی که پیش میآید این است که چرا کتابهای ریاضی تکمیلی هشتم و نهم روی این قضیه تأکید کردهاند.
در ریاضیات دبیرستانی، فقط هندسهٔ اقلیدسی وجود دارد. و در هندسهٔ اقلیدسی، مجموع زاویههای هر مثلث برابر \(180\) درجه است. اما در هندسههای نااقلیدسی، مجموع زاویههای هر مثلث \(180\) درجه نیست! اثبات دیگری برای قضیهٔ ززض وجود دارد که در آن از \(180\) درجه بودن مجموع زاویههای مثلث استفاده نمیشود. و از آن اثبات نتیجه میشود که قضیهٔ ززض در هندسههای نااقلیدسی نیز درست است.
اگر میخواهید دربارهٔ هندسههای نااقلیدسی بیشتر بدانید، و همچین اثبات قضیهٔ ززض (بدون استفاده از قضیهٔ مجموع زاویههای مثلث) را ببینید، کتاب هندسههای اقلیدسی و نااقلیدسی را به شما معرفی میکنم. البته، همیشه در جلساتی که با معلمان (بهویژه معلمان مدارس تیزهوشان) داشتهام، به آنها گفتهام که کسی که میخواهد هندسه درس بدهد، حتماً باید این کتاب (یا کتابی در این سطح) را خوانده باشد …
سلام و عرض ادب خیلی ممنونم از توضیحات کاملتون امروز به معلممان گفتم ایشون گفتن حالت ززض در اخر به همون وز میرسه و من حتما مطالبتون رو برای ایشون میفرستم 🙂
سلام
احتمالاً منظورشون این بوده که حالت وتر و یک ضلع، صورت خاصی از ززض است.
بله ممنونم
همنهشتی مثلث ها به سه صورت
ض ز ض یعنی دوضلع و زاویه بین آنها
ز ض ز یعنی دوزاویه وضلع بین آنها
ض ض ض یعنی سه ضلع
است.
دراین سوال مثلثAHD بنا به حالت همنهشتی
ز ض ز با مثلث ADK همنهشت است.
چگونه؟؟؟؟؟؟؟؟
اثبات این قضیه
?زاویه Hبا زاویه K برابراست
?وتر یعنی AD=AD ضلع مشترک یاوتردومثلث
?زاویه D1=D2
به همین دلیل مثلث ها به حالت ز ض ز
باهم همنهشت اند .
وDH=DK
چرا \(D_1\) با \(D_2\) برابر است؟ (دلیل را بنویسید.)
چون در کتاب درسی همان سه حالت را نوشته و معلمتان هم فقط همان سه حالت را به شما گفته، دلیل نمیشود که حالت دیگری وجود نداشته باشد.
با درود و سلام سپاس از مطالب ارزنده و بحث تقابلی جالب شما …
همانطور که بهتر میدانید مثلث قائم الزاویه نوع خاصی از مثلث هست و در این مسئله خاص برابری D1و D2 هم خوب در چهار چوب هندسه اقلیدسی که مبنای کتابهای درسی هست و با توجه به مجموع زوایای داخلی که برابر ۱۸۰ میباشد اثبات میگردد! چون نقطه واقع روی نیمساز بوده پس دو زاویه راس برابرند ، دو زاویه دیگر هم که قائمه هستند و برابر پس زاویه سوم یعنی D1=D2 خواهد بود !
آنجه شما نوشتهاید همان اثبات قضیهٔ ززض است.
سلام.منظور از عکس قضیه نیمساز که مثلا نقطه ای به نام nاز دو ضلع زاویه m فاصله یکسان دارد چیست؟
سلام
«فاصله» یعنی طول پارهخطی که از آن نقطه بر ضلع زاویه عمود میشود.
اگه زاویه 90 درجه درست نشه یعنی اگه HوK زاویه باز داشتن چطوری باید ثابت کنیم؟
نمیشه زاویهٔ 90 درجه دست نشه؛ چون از هر نقطه خارج از یک خط میتوان عمودی بر آن خط رسم کرد.
اقا قضیه نیم ساز ها که این نیست .
اون تو مثلثه .
این قضیهٔ نیمساز است، نه قضیهٔ نیمسازها.
آیا منظور شما از قضیهٔ نیمسازها، قضیهٔ همرسی نیمسازهاست؟
مگه am وتر نیس؟
پارهخط \(AM\) وتر مثلثهای قائمالزاویهٔ \(AMK\) و \(AMH\) است.
نیمخط \(AM\) نیمساز زاویهٔ \(KAH\) است.
پس حالت وز هم درسته؟
حالت وز که احتمالاً منظورتون وتر و یک زاویه است، حالت خاصی از حالت ززض در مثلثهای قائمالزاویه است.
لطفاً متن زیر را بخوانید و کمی فکر کنید.
در همهٔ مثلثها، اگر دو زاویه و ضلع غیر بین آنها از یک مثلث نظیر به نظیر با دو ضلع و زاویهٔ غیر بین آنها از مثلث دیگر برابر باشد، آنوقت زاویهٔ سوم هم برابر است. (برای مشاهدهٔ اثبات، اینجا را کلیک کنید.) پس دو مثلث همنهشت هستند. (به این حالت میگوییم ززض)
عجیب است که کتابهای درسی حالتی ساختهاند بهنام وز! یعنی اگر در دو مثلث قائمالزاویه، دو زاویه (زاویهٔ قائمه و یک زاویهٔ حاده) و وتر (که ضلع غیر بین آن دو زاویه است) برابر باشند، آنوقت دو مثلث قائمالزاویه همنهشتاند.
پس وز همان حالت ززض است ولی در مثلث قائمالزاویه. وقتی میدانیم چنین چیزی در همهٔ مثلثها درست است، و اثبات آن هم بسیار ساده است، چرا باید فقط در مثلثهای قائمالزاویه از آن استفاده کنیم و …
در قضیه نیم ساز آیا این دو مثلث در حالت وز یا ز ض ز هم مشترکند درسته؟
حالت وز حالت خاص قضیهٔ ززض است. قضیهٔ ززض با استفاده از قضیهٔ زضز نتیجه میشود. لطفاً یکبار اثبات آنها را در قضیههای هندسه بخوانید.
حالت وز خیلی مسخره است!! ما میدانیم که همهٔ مثلثها در حالت ززض همنهشتاند. حالت وز، در واقع همان حالت ززض در مثلث قائمالزاویه است (برابری وترها، یک زاویهٔ تند، و یک زاویهٔ قائمه). چرا باید در مثلث قائمالزاویه برای حالت ززض، اسم دیگری بگذاریم؟!
احسنتم