مطالب تدریس شده در کلاس

1. اگر برای سه عدد اول $a$، $b$، و $c$ بدانیم که

$$a=\frac{xy+3}{y},\;b=\frac{xy+2y+3}{y},\;c=\frac{xy+4y+3}{y}$$
آنگاه مقدار عددی $a^2+b^2-c^2$ را به‌دست آورید.

پاسخ را نشان بده!

$b=a+2$. (چرا؟)

چرا؟

$$\begin{aligned}b&=\frac{xy+2y+3}{y}\\&=\frac{xy+3}{y}+\frac{2y}{y}\\&=\frac{xy+3}{y}+2\\&=a+2.\end{aligned}$$

$c=a+4$.
چرا؟

$$\begin{aligned}b&=\frac{xy+4y+3}{y}\\&=\frac{xy+3}{y}+\frac{4y}{y}\\&=\frac{xy+3}{y}+4\\&=a+4.\end{aligned}$$

اگر هر سه عدد $a$، $a+2$، و $a+4$ اول باشند، آنگاه $a=3$.
چرا؟

برای عدد $a$ سه حالت وجود دارد:
حالت اول. باقی‌ماندهٔ تقسیم عدد $a$ بر ۳ برابر صفر است.
حالت دوم. باقی‌ماندهٔ تقسیم عدد $a$ بر ۳ برابر ۱ است.
حالت سوم. باقی‌ماندهٔ تقسیم عدد $a$ بر ۳ برابر ۲ است.

در حالت اول، چون می‌دانیم $a$ عددی اول است، پس $a=3$. در نتیجه $a+2=5$ و $a+4=7$.
در حالت دوم، باقی‌ماندهٔ تقسیم $a+2$ بر ۳ برابر صفر می‌شود(؟) و چون می‌دانیم $a+2$ عددی اول است پس $a+2=3$ و در نتیجه $a=1$. از طرفی می‌دانیم $a$ نیز عددی اول است؛ پس این حالت اتفاق نمی‌افتد.
در حالت سوم، باقی‌ماندهٔ تقسیم $a+4$ بر ۳ برابر صفر می‌شود(؟) و چون می‌دانیم $a+4$ عددی اول است پس $a+4=3$ و در نتیجه $a=-1$. از طرفی می‌دانیم $a$ عددی اول است؛ پس این حالت اتفاق نیز نمی‌افتد.

بنابراین $a^2+b^2-c^2=-15$.
چرا؟

$$\begin{aligned}a^2+b^2-c^2&=3^2+5^2-7^2\\&=9+25-49\\&=34-49\\&=-15.\end{aligned}$$

---

2. اگر $n$ یک عدد صحیح مثبت باشد، نماد $n!$ (می‌خوانیم: «$n$ فاکتوریِل»)، برای نشان دادن ضرب اعداد صحیح $1$ تا $n$ استفاده می‌شود. برای مثال:$$5! = 1 \times 2 \times 3 \times 4 \times 5 = 120.$$ حاصل کدام گزینه‌ (گزینه‌های) زیر مربع کامل است؟

الف)‌ $\dfrac{(20!) (19!)}{1}$

ب) $\dfrac{(20!) (19!)}{2}$

ج) $\dfrac{(20!) (19!)}{3}$

د) $\dfrac{(20!) (19!)}{4}$

هـ) $\dfrac{(20!) (19!)}{5}$

پاسخ را نشان بده!

توجه کنید که در همه گزینه‌ها صورت کسر برابر است با $(20!) (19!)$.
چون $20!$ برابر است با حاصل‌ضرب اعداد صحیح $1$ تا $20$، می‌توانیم بگوییم که $20!$ برابر است با:
$$\begin{aligned}&(1\times2\times3\times\dots\times19)\times20\\&=19!\times20.\end{aligned}$$پس صورت کسرها (که در همۀ گزینه‌ها مشترک است) را به‌صورت زیر می‌نویسیم:
$$(19!\times 20) (19!) = (19!)^2 \times 20.$$

حال گزینه‌ها را بررسی می‌کنیم:
$$\begin{aligned}&\frac{(20!) (19!)}{1}=\frac{(19!)^2\times20}{1} = (19!)^2 \times 20\\[7pt]&\frac{(20!) (19!)}{2}=\frac{(19!)^2\times20}{2}= (19!)^2 \times 10\\[7pt]&\frac{(20!) (19!)}{3}=\frac{(19!)^2\times20}{3} = (19!)^2 \times \frac{20}{3}\\[7pt]&\frac{(20!) (19!)}{4} = \frac{(19!)^2\times20}{4} =(19!)^2 \times 5\\[7pt]&\frac{(20!) (19!)}{5}=\frac{(19!)^2\times20}{5} = (19!)^2 \times 4.\end{aligned}$$
حاصل‌ضرب یک عدد مربع کامل در یک عدد صحیح مثبت مانند $a$، مربع کامل است، هرگاه $a$ خودش مربع کامل باشد. بنابراین، چون در بین اعداد $20$، $10$، $\frac{20}{3}$، $5$، و $4$، فقط $4$ مربع کامل است، پس در بین گزینه‌های داده شده، فقط $(19!)^2 \times 4$ یا $\frac{(20!) (19!)}{5}$ مربع کامل است.

---

3. به یک زوج $(m,n)$ یک زوج شاد گوییم هرگاه بزرگ‌ترین مقسوم‌علیه مشترک $m$ و $n$ یک عدد مربع کامل باشد. برای مثال $(20,24)$ یک زوج شاد است زیرا بزرگ‌ترین مقسوم‌علیه مشترک $20$ و $24$، عدد $4$ است. فرض کنید $k$ یک عدد صحیح مثبت باشد به‌طوری‌که $(205800,35k)$ یک زوج شاد است. چند حالت‌ ممکن برای $k$ که $k \leq 2940$ وجود دارد؟
پاسخ را نشان بده!

قبل از شروع راه حل، پنج نکته از تجزیهٔ اعداد طبیعی به عوامل اول را باهم مرور می‌کنیم:
پنج نکته دربارهٔ تجزیهٔ اعداد طبیعی

نکتهٔ اول. هر عدد صحیح مثبت بزرگ‌تر از $1$ را می‌توان به صورت حاصل ضرب یکتایی از اعداد اول نوشت. (اگر خود عدد صحیح مثبت، اول باشد، حاصل مورد نظر خود این عدد است.) این نکته «قضیه‌ٔ اساسی حساب» نام دارد. برای مثال:
$$1500=2^{2}\times 3^{1} \times 5^{3}$$ و هیچ راه دیگری وجود ندارد که بتوانیم $1500$ را تجزیه کنیم. توجه کنید که تغییر دادن ترتیب این اعداد، نمی‌تواند تجزیه‌ٔ دیگری را به وجود آورد.

نکتهٔ دوم. اگر $n$ یک عدد صحیح مثبت باشد و $d$ یک مقسوم‌علیه صحیح مثبت $n$ باشد، آنگاه تنها عوامل اول $d$، حتماً عوامل اول $n$ نیز هستند.
برای مثال، اگر $d$ یک مقسوم‌علیه مثبت $n=1500$ باشد، آنگاه تنها اعداد اولی که در تجز‌یه‌ٔ $d$ می‌توانند وجود داشته باشند، $2$، $3$، و $5$ هستند. برای مثال، $d$ نمی‌تواند بر $7$ یا $11$ یا هر عدد اول دیگری که برابر با $2$، $3$، یا $5$ نیست، بخش‌پذیر باشد. $d$ ممکن است بر $2$، $3$، یا $5$ بخش‌پذیر باشد و یا ممکن است بر بعضی از آن‌ها بخش‌پذیر نباشد.

نکتهٔ سوم. اگر $n$ یک عدد صحیح مثبت، $d$ یک مقسوم‌علیه صحیح مثبت $n$، و $p$ یک عامل اول برای $d$ و $n$ باشد، آنگاه توان $p$ در تجزیهٔ عدد $d$ کوچکتر یا مساوی توان $p$ در تجزیهٔ عدد $n$ است.
برای مثال، اگر $d$ بر $5$ بخش‌پذیر و $d$ یک مقسوم‌علیه $n=1500=2^{2} \times 3^{1} \times 5^{3}$ باشد، آنگاه $d$ فقط می‌تواند بر $5$ یا $5^{2}$ یا $5^{3}$ بخش‌پذیر باشد و نمی‌تواند بر $5^{4}$ یا $5^{5}$ یا هر توان بزرگ‌تری از $5$ بخش‌پذیر شود.

نکتهٔ چهارم. فرض کنید $m$ یک عدد صحیح مثبت بزرگ‌تر از $1$ باشد. عدد $m$ یک مربع کامل است اگر و تنها اگر توان هر عدد اولی که در تجزیه‌اش قرار دارد برابر با یک عدد زوج باشد.
برای مثال، $n=1500=2^{2} \times 3^{1} \times 5^{3}$ یک مربع کامل نیست اما $m=22500=2^{2} \times 3^{2} \times 5^{4}$ یک مربع کامل است.
توجه کنید که اگر $m$ یک مربع کامل باشد، آنگاه عدد صحیح مثبتی مانند $r$ وجود دارد به‌طوری‌که $m=r^{2}$. بنابراین می‌توانیم در تجزیه‌ٔ ‏$m$، عامل‌های اول $r$ را دوبار بنویسیم.
برای مثال، اگر
$$r=150=2^{1} \times 3^{1} \times 5^{2}$$آنگاه
$$\begin{aligned}m&=2^{1} \times 3^{1} \times 5^{2} \times 2^{1} \times 3^{1} \times 5^{2}\\& = 2^{2} \times 3^{2} \times 5^{4}.\end{aligned}$$
به علاوه اگر عامل‌های اول $m$ شامل یک عدد اول با توان فرد باشد، آنگاه واضح است که $\sqrt{m}$ یک عدد صحیح نیست؛ و در نتیجه، $m$ مربع کامل نیست.

نکتهٔ پنجم. یک روش برای پیدا کردن بزرگ‌ترین مقسوم‌علیه مشترک (ب‌م‌م) دو عدد صحیح مثبت $n$ و $t$ این است که تجزیه‌ شدهٔ $n$ و $t$ را بنویسیم و عدد صحیح مثبت $d$ (ب‌م‌م) را طوری بسازیم که برای هر پایه‌ٔ اول مشترک، هرکدام را که توان کمتری دارد به کار بگیریم. برای مثال، اگر
$$n=1500=2^{2}\times 3^{2} \times 5^{3}$$و
$$t=7000=2^{3}\times 5^{3} \times 7^{1}$$آنگاه بزرگ‎ترین مقسوم‌علیه مشترک $n$ و $t$ برابر است با $2^{2} \times 5^{3}=500$. دلیل این روش بر اساس نکته‌ٔ دوم (چون $d$ یک مقسوم‌علیه مشترک $n$ و $t$ است، فقط می‌تواند شامل اعداد اول مشترک در این دو لیست باشد) و نکته‌ٔ سوم ($d$ نمی‌تواند شامل عدد اولی با توان‌های بزرگ‌تر از توان‌های $n$ و $t$ باشد) است.

حال، به حل مسئله می‌پردازیم.

فرض کنید زوج $(205800, 35k)$ یک زوج شاد باشد.
عدد $205800$ را تجزیه می‌کنیم:
$$\begin{aligned}205800&=2058 \times 100\\&= 2 \times 1029 \times (2\times 5)^{2}\\&=2\times 3 \times 343 \times 2^{2} \times 5^{2}\\&=2 \times 3 \times 7^{3} \times 2^{2} \times 5^{2}\\&=2^{3} \times 3^{1} \times 5^{2} \times 7^{3}.\end{aligned}$$
همچنین، توجه کنید که
$$35k = 5^{1} \times 7^{1} \times k.$$
عدد $d$ را به عنوان بزرگ‌ترین مقسوم‌علیه مشترک $205800$ و $35k$ در نظر بگیرید. می‌خواهیم همهٔ حالت‌های ممکن برای $k\leq 2940$ را پیدا کنیم به‌طوری‌که $d$ یک مربع کامل باشد.
چون هم $5$ و هم $7$ مقسوم‌علیه‌های اول $205800$ و $35k$ هستند، بنابراین $5$ و $7$، هر دو مقسوم‌علیه‌های اول $d$ هم هستند. (بر اساس نکته‌ٔ پنجم)
برای اینکه $d$ یک مربع کامل باشد، باید در تجزیه شدهٔ عدد $d$، توان $5$ و $7$ زوج باشد. (بر اساس نکته‌ٔ چهارم)
از آنجایی که توان‌های $5$ و $7$ در $205800$، $5^{2}$ و $7^{3}$ هستند، برای اینکه $d$ مربع کامل باشد باید در تجزیهٔ شدهٔ $d$، اعداد $5^{2}$ و $7^{2}$ وجود داشته باشد.
چون
$$d=5\times 7 \times k$$
بنابراین برای برخی مقادیر صحیح و مثبت $j$،
$$k=5\times 7 \times j = 35j.$$از طرفی، داریم:
$$\begin{aligned}&k \leq 2940 \\&\Rightarrow 35j \leq 2940 \\&\Rightarrow j \leq 84\end{aligned}$$
می‌دانیم $d$ بزرگ‌ترین مقسوم‌علیه مشترک دو عدد $2^{3} \times 3^{1} \times 5^{2} \times 7^{3}$ و $5^{2} \times 7^{2} \times j$ است.
اکنون، چه اطلاعات بیشتری می‌توانیم از $j$ به دست بیاوریم؟
$\bullet$ $j$ نمی‌تواند بر $3$ بخش‌پذیر باشد.
چرا؟

اگر $j$ بر $3$ بخش‌پذیر باشد، آنگاه در تجزیهٔ شدهٔ $d$ عدد $3^{1}$ وجود خواهد داشت (چون هم $205800$ و هم $35k$ می‌توانند بر $3$ بخش‌پذیر شوند)؛ ولی در تجزیه شدهٔ $d$ نمی‌تواند $3^{2}$ وجود داشته باشد (زیرا $205800$ بر $3^2$ بخش‌پذیر نیست). یعنی $d$ نمی‌تواند مربع کامل باشد.

$\bullet$ $j$ نمی‌تواند بر $7$ بخش‌پذیر باشد.
چرا؟

اگر $j$ بر $7$ بخش‌پذیر باشد، آنگاه $7^{3}$ در تجزیه شدهٔ $d$ وجود خواهد داشت. در نتیجه، $d$ نمی‌تواند یک مربع کامل باشد.

$\bullet$ اگر $j$ بر $2$ بخش‌پذیر باشد آنگاه $2^{2}$ در تجزیه‌ شدهٔ عدد $j$ وجود خواهد داشت. توجه کنید که در این حالت، چون $d$ باید مربع کامل باشد، $2^{1}$ یا $2^{3}$ نمی‌تواند در تجزیهٔ شدهٔ عدد $j$ وجود داشته باشد.

$\bullet$ $j$ می‌تواند بر $5$ بخش‌پذیر باشد.
چرا؟

اگر $j$ بر $5$ بخش‌پذیر باشد، توان $5$ در $d$ قبلاً به‌وسیلهٔ توان $5$ در $205800$ محدود شده است. (یعنی در تجزیه شدهٔ $d$، توان $5$ باید برابر $2$ باشد و نه بیشتر!)

$\bullet$ $j$ می‌تواند بر اعداد اول دیگری به جز $2$، $3$، $5$، یا $7$ بخش‌پذیر باشد.
چرا؟

چون عامل‌های اول $205800$ فقط $2$، $3$، $5$، و $7$ هستند، پس اگر $j$ بر اعداد اول دیگری بخش‌پذیر باشد، تأثیری در $d$ نخواهد داشت.

با توجه به اطلاعات بالا، دو حالت برای $j$ وجود دارد.
حالت اول. $j$ بر $2^{2}$ بخش‌پذیر باشد ولی بر توان بزرگ‌تر از آن بخش‌پذیر نباشد. در این حالت، $6$ مقدار مختلف برای $j$ وجود دارد.
چرا؟

در اینجا برای برخی مقادیر صحیح مثبت فرد $h$،
$$j=2^{2}h=4h$$
داریم:
$$\begin{aligned}&j \leq 84\\&\Rightarrow 4h \leq 84\\&\Rightarrow h \leq 21\end{aligned}$$
چون $j$ نمی‌تواند بر $3$ یا $7$ بخش‌پذیر باشد، پس همهٔ مقادیر ممکن برای $h$ عبارتند از:
$$1,5,11,13,17,19.$$
هرکدام از این مقادیر $h$ می‌توانند یک $j$ تولید کنند. بنابراین، $6$ مقدار مختلف برای $j$ به‌دست می‌آید:
$$4,20,44,52,68,76.$$

حالت دوم. $j$ بر $2$ بخش‎پذیر نباشد. در این‌ حالت، $24$ مقدار مختلف برای $j$ وجود دارد.
چرا؟

در این حالت، $j$ عددی فرد است. از طرفی، چون $j$ نمی‌تواند بر $3$ یا $7$ بخش‌پذیر باشد و $j \leq 84$، بنابراین همهٔ مقادیر ممکن برای $j$ عبارتند از:
$$1,5,11,13,17,19,23,25,29,31,37,41,43,47,53,55,59,61,65,67,71,73,79,83.$$

بنابراین در مجموع، $30$ مقدار ممکن برای $j$ وجود دارد و درنتیجه $30$ مقدار ممکن برای $k \leq 2940$ داریم که باعث شوند زوج $(205800,35k)$ یک زوج شاد باشد.

---

4. اگر $a$، $b$، و $c$ سه عدد طبیعی باشند، کدام‌یک از معادله‌های زیر جواب دارد؟

معادلهٔ اول: $\dfrac{41}{42}=\dfrac{1}{a}+\dfrac{1}{b}$

معادلهٔ دوم: $\dfrac{41}{42}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}$

پاسخ را نشان بده!

معادلهٔ اول جواب ندارد؛ زیرا:

$\bullet$ اگر هر دو عدد طبیعی $a$ و $b$ بزرگتر یا مساوی $3$ باشند، آنگاه معادلهٔ اول جواب ندارد. (چرا؟)

چرا؟

اگر $a\geq 3$ و $b\geq 3$، آنگاه $\frac{1}{a}\leq \frac{1}{3}$ و $\frac{1}{b}\leq\frac{1}{3}$. بنابراین:
$$\frac{1}{a}+\frac{1}{b}\leq \frac{1}{3}+\frac{1}{3}=\frac{2}{3}$$
از طرفی، چون $\dfrac{2}{3}<\dfrac{41}{42}$، پس
$$\frac{1}{a}+\frac{1}{b}<\frac{41}{42}$$

$\bullet$ اگر یکی از مقادیر $a$ یا $b$ برابر $2$ باشد، آنگاه معادلهٔ اول جواب طبیعی ندارد.

چرا؟

فرض کنید $a=2$. دراین‌صورت داریم:
$$\begin{aligned}&\frac{1}{a}+\frac{1}{b}=\frac{41}{42}\\[7pt]&\Rightarrow\frac{1}{2}+\frac{1}{b}=\frac{41}{42}\\[7pt]&\Rightarrow\frac{1}{b}=\frac{41}{42}-\frac{1}{2}\\[7pt]&\Rightarrow\frac{1}{b}=\frac{41}{42}-\frac{21}{42}\\[7pt]&\Rightarrow\frac{1}{b}=\frac{20}{42}\\[7pt]&\Rightarrow\frac{1}{b}=\frac{10}{21}\\[7pt]&\Rightarrow b=\frac{21}{10}.\end{aligned}$$

$\bullet$ اگر یکی از مقادیر $a$ یا $b$ برابر $1$ باشد، آنگاه معادلهٔ اول جواب طبیعی ندارد.
چرا؟

فرض کنید $a=1$. دراین‌صورت داریم:
$$\begin{aligned}&\frac{1}{a}+\frac{1}{b}=\frac{41}{42}\\[7pt]&\Rightarrow\frac{1}{1}+\frac{1}{b}=\frac{41}{42}\\[7pt]&\Rightarrow\frac{1}{b}=\frac{41}{42}-1\\[7pt]&\Rightarrow\frac{1}{b}=-\frac{1}{42}\\[7pt]&\Rightarrow b=-42.\end{aligned}$$

در معادلهٔ دوم باتوجه‌به روش کسر مصری و تمرین ۱۳ صفحهٔ ۱۴ کتاب ریاضیات تکمیلی هشتم، داریم:
$$\frac{41}{42}=\frac{1}{2}+\frac{1}{3}+\frac{1}{7}$$


---

5. «حاصل‌جمع منفی‌مثبتِ» عدد $23485$ برابر است با:
   $$2-3+4-8+5=0.$$در حالت کلی، برای به‌دست آوردن حاصل‌جمع منفی‌مثبتِ یک عدد طبیعی، بین رقم‌های آن عدد، از چپ به راست و یکی‌درمیان، علامت‌های $-$ و $+$ قرار می‌دهیم و حاصل عبارت را محاسبه می‌کنیم.
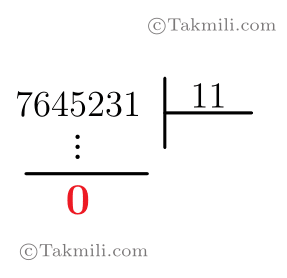
   یک عدد طبیعی بر $11$ بخش‌پذیر است هروقت حاصل‌جمع منفی‌مثبتِ آن عدد بر $11$ بخش‌پذیر باشد. برای مثال، عدد $23485$ بر $11$ بخش‌پذیر است، چون حاصل‌جمع‌ منفی‌مثبتِ $23485$ برابر $0$ است و $0$ بر $11$ بخش‌پذیر است. همچنین، $92807$ بر $11$ بخش‌پذیر است چون حاصل‌جمع منفی‌مثبتِ $92807$ برابر $22$ است و $22$ بر $11$ بخش‌پذیر است. اما $60432$ بر $11$ بخش‌پذیر نیست چون حاصل‌جمع منفی‌مثبتِ $60432$ برابر $9$ است و $9$ بر $11$ بخش‌پذیر نیست.

   

   با ارقام $1$، $2$، $3$، $4$، $5$، $6$، و $7$ چند عدد هفت‌رقمی می‌توان ساخت که بر $11$ بخش‌پذیر باشد؟ (تکرار ارقام مجاز نیست.)

پاسخ را نشان بده!

فرض کنید عدد هفت رقمی $\overline{abcdefg}$ بر $11$ بخش‌پذیر باشد. در این صورت، اگر
$$P=a-b+c-d+e-f+g$$آن‌وقت $P$ باید بر $11$ بخش‌پذیر باشد.

اگر $M=a+c+e+g$ و $N=b+d+f$، آن‌وقت داریم:
$$\begin{aligned}P&=a-b+c-d+e-f+g\\&=(a+c+e+g)-(b+d+f)\\&=M-N.\quad(1)\end{aligned}$$
همچنین داریم:
$$\begin{aligned}M+N&=(a+c+e+g)+(b+d+f)\\&=1+2+3+4+5+6+7\\&=28.\quad(2)\end{aligned}$$

حال، بیشترین و کمترین مقدار ممکن برای $P$ را به‌دست می‌آوریم.

$\bullet$ بیشترین مقدار ممکن برای $P$ برابر $16$ است.

چرا؟

بیشترین مقدار ممکن برای $M$ برابر است با:
$$7+6+5+4=22.$$
و اگر $M$ بیشترین مقدار ممکن را داشته باشد، آن‌وقت $N$ کمترین مقدار ممکن را خواهد داشت:
$$3+2+1=6.$$
در چنین شرایطی، با توجه به رابطهٔ $(1)$، $P$ بیشترین مقدار ممکن را دارد:
$$\begin{aligned}P&=M-N\\&=22-6\\&=16.\end{aligned}$$

$\bullet$ کمترین مقدار ممکن برای $P$ برابر $-8$ است.

چرا؟

بیشترین مقدار ممکن برای $N$ برابر است با:
$$7+6+5=18.$$
و اگر $N$ بیشترین مقدار ممکن را داشته باشد، آن‌وقت $M$ کمترین مقدار ممکن را خواهد داشت:
$$4+3+2+1=10.$$
در چنین شرایطی، با توجه به رابطهٔ $(1)$، $P$ کمترین مقدار ممکن را دارد:
$$\begin{aligned}P&=M-N\\&=10-18\\&=-8.\end{aligned}$$

بنابراین، چون $P$ باید بر $11$ بخش‌پذیر باشد و $-8\leq P\leq16$، پس دو حالت برای $P$ وجود دارد: $P=11$ و $P=0$.
حالت اول. $P$ نمی‌تواند برابر $11$ باشد.

چرا؟

اگر $P$ برابر $11$ باشد، آن‌وقت چون بنابه رابطهٔ $(1)$ داریم: $$P=M-N=11.$$ پس یکی از مقدارهای $M$ یا $N$ زوج است و دیگری فرد.
از طرفی، بنابه رابطهٔ $(2)$ داریم: $$M+N=28.$$ پس $M$ و $N$ یا هر دو زوج هستند یا هر دو فردند.
در نتیجه، $P$ نمی‌تواند عددی فرد باشد.

حالت دوم. اگر $P=0$، آن‌وقت $M=14$ و $N=14$.

چرا؟

اگر $P=0$، آن‌وقت از رابطهٔ $(1)$ نتیجه می‌شود:
$$\begin{aligned}&P=M-N=0\\&\Rightarrow M=N.\end{aligned}$$
از طرفی، بنابه رابطهٔ $(2)$ می‌دانیم $M+N=28$. بنابراین:
$$M=N=14.$$

دقیقاً چهار حالت وجود دارد که می‌توان $14$ را به‌صورت مجموع سه عدد طبیعی کوچکتر یا مساوی $7$ نوشت:
$$\begin{aligned}14&=7+6+1\\&=7+5+2\\&=7+4+3\\&=6+5+3.\end{aligned}$$
اگر $b$، $d$، و $f$، (نه لزوماً به‌ترتیب) برابر $7$، $6$، و $1$ باشند، آن‌وقت $a$، $c$، $e$، و $g$، (نه لزوماً به‌ترتیب) برابر $5$، $4$، $3$، و $2$ خواهند بود. دراین‌حالت، $144$ عدد هفت رقمی $\overline{abcdefg}$ وجود دارد که بر $11$ بخش‌پذیر است.

چرا؟

در این حالت، در واقع می‌خواهیم تعداد اعداد هفت رقمی‌ مانند $\overline{abcdefg}$ را بشماریم که هریک از مقدارهای $b$، $d$، و $f$ از رقم‌های $7$، $6$، یا $1$ انتخاب شده باشند (و تکرار ارقام مجاز نباشد)، و هریک از مقدارهای $a$، $c$، $e$، و $g$ از رقم‌های $5$، $4$، $3$، یا $2$ انتخاب شده باشند (و تکرار ارقام مجاز نباشد). بنابراین، تعداد این اعداد برابر است با:
$$(3\times2\times1)\times(4\times3\times2\times1)=144.$$

واضح است که برای هریک از سه حالت دیگر نیز، $144$ عدد هفت رقمی $\overline{abcdefg}$ وجود دارد که بر $11$ بخش‌پذیر است.

بنابراین، جواب مسئله برابر است با:
$$4\times144=576.$$

---

پرسش. با ارقام $1$، $2$، $3$، $4$، $5$، $6$، $7$، $8$، و $9$ یک عدد نُه رقمی تصادفی ساخته‌اند به‌طوری‌که تکرار ارقام مجاز نبوده است. احتمال اینکه این عدد هفت رقمی بر $11$ بخش‌پذیر باشد، چقدر است؟

---

تمرین‌های روزانه

1. یسنا $n$ عدد صحیح مثبت متوالی را به‌صورت زیر نوشته است:

$$1,2,3,4,\dots,n-1,n.$$ او $4$ عدد صحیح متفاوت $p$، $q$، $r$، و $s$ را از این اعداد حذف می‌کند. حداقل $3$تا از این $4$ عدد ($p$، $q$، $r$، و $s$) متوالی هستند و شرط زیر برای آن‌ها برقرار است:
$$100 < p < q < r < s.$$
میانگین اعداد صحیح باقی‌مانده برابر $89.5625$ است. تعداد مقادیر ممکن برای $s$ چندتاست؟

پاسخ را نشان بده!

وقتی یسنا $4$ عدد صحیح را از بین اعداد نوشته شده ($n$ عدد) حذف می‌کند، $n-4$ عدد صحیح باقی می‌ماند. فرض می‌کنیم مجموع $n-4$ عدد صحیح باقی مانده برابر $T$ باشد. میانگین این $n-4$ عدد صحیح برابر است با:
$$\begin{aligned}89.5625&=89+0.5+0.0625\\[7pt]&=89+\frac{1}{2}+\frac{1}{16}\\[7pt]&=\frac{1433}{16}.\end{aligned}$$
مجموع $n-4$ عدد صحیح برابر $T$ است، پس می‌توانیم میانگین آن‌ها را به صورت زیر بنویسیم:
$$\begin{aligned}&\frac{T}{n-4}=\frac{1433}{16}\\&\Rightarrow16T=1433(n-4).\end{aligned}$$ چون $1433$ و $16$ هیچ مقسوم‌علیه مشترک بزرگتر از $1$ ندارند (مقسوم‌علیه‌های مثبت $16$ برابرند با: $1$، $2$، $4$، $8$، و $16$ که هیچ کدام از آن‌ها، به جزء $1$، مقسوم‌علیه $1433$ نیستند)، پس $n-4$ مضربی از $16$ است.
از طرفی، می‌دانیم:\[100 همچنین چون $n$تا عدد صحیحی که یسنا در ابتدا نوشته، اعداد صحیح متوالی هستند که از $1$ شروع می‌شوند و تنها $4$ عدد از اعداد بزرگتر از $100$ حذف می‌شوند، پس می‌توان گفت میانگین $n$ عدد و $n-4$ عدد نسبتاً به یکدیگر نزدیک است.
چون میانگین اعداد باقی مانده برابر $89.5625$ است و به $90$ نزدیک است، منطقی است اگر بگوییم میانگین $n$ عدد که در ابتدا داشتیم نیز به $90$ نزدیک است.
چون $n$ عدد صحیح که یسنا در ابتدا نوشته، اعداد صحیح متوالی هستند که از $1$ شروع می‌شوند، می‌توانیم حدس بزنیم که تعداد این $n$ عدد صحیح تقریباً برابر $180$ است. به عبارت دیگر، به نظر می‌رسد که $n$ به $180$ نزدیک است.
همچنین گفتیم که $n-4$ مضربی از $16$ است. نزدیکترین مضرب $16$ به $180$ برابر است با: $160$، $176$، و $192$ پس: $$n=164,\;n=180,\;n=196.$$ فرض می‌کنیم $n=180$، که به نظر می‌رسد نزدیکترین جواب باشد. در انتها نیز نشان می‌دهیم که تنها مقدار ممکن برای $n$ است.
با توجه به معادلۀ زیر:
$$\frac{T}{n-4}=89.5625,$$خواهیم داشت:
$$T=176\times 89.5625=15763.$$ مجموع $n$ عدد صحیح (متوالی) برابر است با:
$$1+2+3+4+\dots+(n-1)+n=\frac{1}{2}n(n+1).$$ وقتی $n=180$، مجموع $180$ عدد صحیح (متوالی) زیر:
$$1,2,3,\dots,178,179,180$$برابر است با:
$$\frac{1}{2}(180)(181)=16290.$$ چون مجموع $180$ عدد برابر است با $16290$ و مجموع اعداد وقتی $4$ عدد را حذف می‌کنیم برابر است با $15763$، پس مجموع $4$ عدد حذف شده برابر است با:
$$16290-15763=527.$$یعنی:
$$p+q+r+s=527.$$حال می‌خواهیم تعداد حالاتی که می‌توانیم $4$ عدد $p$، $q$، $r$، و $s$ را با شرایط زیر انتخاب کنیم، بشماریم:
$\bullet$ $100 < p < q < r < s\leq 180$
$\bullet$ $p+q+r+s=527$
$\bullet$ حداقل $3$ تا از $4$ عدد $p$، $q$، $r$ و $s$ متوالی باشند.
چهارمین عدد از این $4$ عدد صحیح حداقل برابر $101$ و حداکثر برابر $180$ است، یعنی مجموع $3$ عدد متوالی حداقل برابر است با:
$$527-180=347.$$ و حداکثر برابر است با:
$$527-101=426.$$ یعنی $3$ عدد متوالی حداقل برابرند با اعداد $115$، $116$، و $117$ (که مجموعشان برابر $348$ است) ، چون اگر اعداد $114$، $115$، و $116$ را انتخاب کنیم، مجموعشان برابر است با:
$$114+115+116=345,$$ که مجموعشان کوچک است و اگر اعداد کوچکتر را انتخاب کنیم، مجموعشان نیز کوچکتر می‌شود که در این صورت انتخاب این اعداد مناسب نیست.
اگر $p$، $q$، و $r$ به‌ترتیب برابر $115$، $116$ و $117$ باشند، آنگاه:
$$s=527-348=179.$$
سه عدد متوالی حداکثر برابرند با $141$، $142$، و $143$ (مجموعشان برابر است با $426$)؛ چون اگر اعداد $142$، $143$، و $144$ را انتخاب کنیم، مجموعشان برابر است با:
$$142+143+144=429,$$ که مجموعشان بزرگ است و اگر اعداد بزرگتر را انتخاب کنیم، مجموعشان نیز بزرگتر می‌شود که در این صورت انتخاب این اعداد مناسب نیست. اگر $p$، $q$، و $r$ به‌ترتیب برابر $141$، $142$، و $143$ باشند، پس:
$$s=527-426=101.$$
چون هر کدام از $3$ عدد متوالی $1$ واحد افزایش می‌یابند و مجموع اعداد عددی ثابت است، پس چهارمین عدد $3$ واحد کاهش می‌یابد تا مجموع اعداد همچنان ثابت بماند.
با توجه به اطلاعات بالا، حالات ممکن برای $p$، $q$، $r$، و $s$ را در زیر آورده‌ایم:
$$\begin{aligned}&115,116,117,179\;;\;116,117,118,176\;;\;\dots\;;\;130,131,132,134\\&128,132,133,134\;;\;125,133,134,135\;;\;\dots\;;\;101,141,142,143\end{aligned}$$
$26$ حالت مختلف از گروه‌های چهارتایی اعداد صحیح داریم که می‌توانیم از $n$ عدد اولیه حذف کنیم ($16$ حالت در ردیف اول و $10$ حالت در ردیف دوم). مقادیر ممکن برای $s$ عبارتند از:
$$\begin{aligned}&179,176,173,170,167,164,161,158,155,152,149,146,143,140,137,134\\&134,135,136,137,138,139,140,141,142,143\end{aligned}$$ دو ردیف بالا، $4$ عدد مشترک دارند، پس در مجموع $26-4=22$ مقدار ممکن برای $s$ داریم.

چرا $n=180$ تنها مقدار ممکن برای $n$ است؟
پاسخ:

می‌دانیم میانگین دنباله‌ای از اعداد صحیح متوالی که از $a$ شروع می‌شود و در $b$ تمام می‌شود، برابر است با میانگین $a$ و $b$، یعنی $\frac{a+b}{2}$. (این جمله درست است ، چون اختلاف اعداد صحیح داخل دنباله همواره ثابت است و به طور مساوی توزیع شده، پس میانگین اولین و آخرین عدد برابر است با میانگین کل اعداد دنباله.)
پس $n$ عدد که یسنا در ابتدا نوشته بود نیز $(1,2,\dots,n-1,n)$ دارای میانگین زیر هستند:
$$\frac{n+1}{2}.$$ اگر $4$تا از بزرگترین اعداد دنباله را حذف کنیم، اعداد به صورت زیر خواهند شد:
$$1,2,\dots,n-5,n-4$$ که در این صورت میانگین آن‌ها برابر است با:
$$\frac{(n-4)+1}{2}=\frac{n-3}{2}.$$ اگر $4$تا از کوچکترین اعداد دنباله را حذف کنیم، اعداد به صورت زیر خواهند شد:
$$5,6,\dots,n-1,n$$ که در این صورت میانگین آن‌ها برابر است با:
$$\frac{n+5}{2}.$$ با حذف هر $4$ عدد از این اعداد، مجموع اعداد باقی مانده بزرگتر یا مساوی میانگین اعداد زیر می‌شود:
$$1,2,\dots,n-5,n-4$$ و کوچکتر یا مساوی میانگین اعداد زیر می‌شود:
$$5,6,\dots,n-1,n$$ یعنی، میانگین اعداد باقی مانده حداقل برابر $\frac{n-3}{2}$ و حداکثر برابر $\frac{n+5}{2}$ است.
یعنی میانگین $n$ عدد (که برابر است با $89.5625$) بزرگتر یا مساوی $\frac{n-3}{2}$ و کوچکتر یا مساوی $\frac{n+5}{2}$ است. پس خواهیم داشت:
$$\begin{aligned}&89.5625\geq \frac{n-3}{2}\\&\Rightarrow n-3\leq 179.125\\&\Rightarrow n\leq 182.125\end{aligned}$$ و
$$\begin{aligned}&89.5625\leq \frac{n+5}{2}\\&\Rightarrow n+5\geq 179.125\\&\Rightarrow n\geq 174.125\end{aligned}$$
چون $n$ یک عدد صحیح است پس:
$$\begin{aligned}&175\leq n\leq 182\\&\Rightarrow 171\leq n-4 \leq 178.\end{aligned}$$ همچنین $n-4$ مضربی از $16$ است، پس:
$$\begin{aligned}&n-4=176\\&\Rightarrow n=180.\end{aligned}$$

---

2. مسائل زیر، با توجه به مرحلهٔ آلفا بازی Euclidea طرح شده‌اند. ابتدا هریک از این مسائل را حل کنید و سپس، سعی کنید مسائل دیگری برای هریک از مراحل بازی بسازید.

مسئله ۱. در شکل زیر، دو دایره به مرکز $A$ و $B$ رسم شده است. شعاع دو دایره برابر است. چرا مثلث‌های $ABC$ و $ABD$ متساوی‌الاضلاع هستند؟



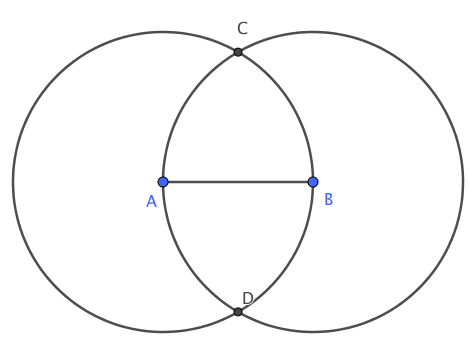
مسئله ۲. در شکل زیر، دو دایره به مرکز $A$ و $B$ رسم شده است. شعاع دو دایره برابر است. چرا خط $CD$ عمودمنصف پاره‌خط $AB$ است؟



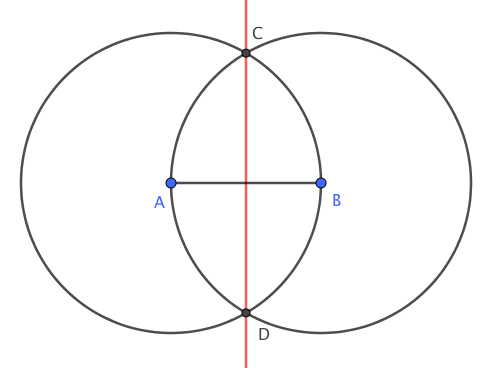
مسئله ۳. در شکل زیر، $ABCD$ مستطیل و $EF$ عمودمنصف قطر $AC$ است. چرا چهارضلعی $AECF$ لوزی است؟



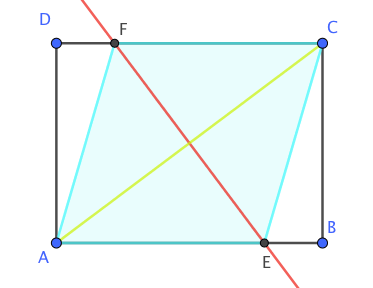
مسئله ۴. عمودمنصف‌های دو وتر غیر موازی از یک دایره، یکدیگر را در نقطهٔ $C$ قطع کرده‌اند. چرا $C$ مرکز دایره است؟

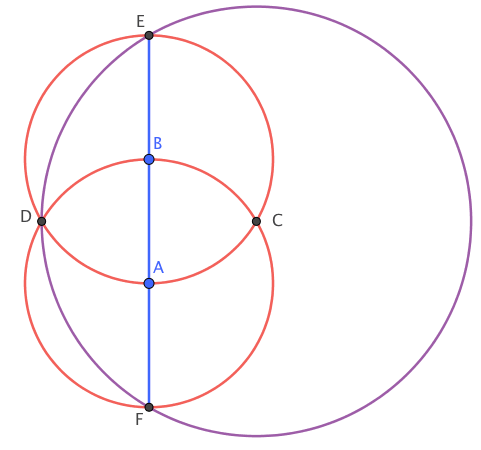
مسئله ۵. در شکل زیر، دو دایره به مرکز $A$ و $B$ رسم شده است. شعاع این دو دایره یکسان هستند. پاره‌خط $EF$ قطر مشترک دو دایره است. چرا اگر دایره‌ای به مرکز $C$ و شعاع $CD$ رسم کنیم، از نقاط $E$ و $F$ می‌گذرد؟



---