نام کاربری و رمز عبور شما، شماره موبایل ارائه شده در زمان ثبت‌نام به همراه “0” اول شماره است.
لینک جلسات
هفته اول هفته دوم هفته سوم هفته چهارم هفته پنجم هفته ششم هفته هفتم هفته هشتم هفته نهم هفته دهممسائل هفتهٔ اول
از راه‌حل‌های تشریحی خود عکس بگیرید و آنها را در بخش کامنت‌های همین صفحه آپلود کنید.
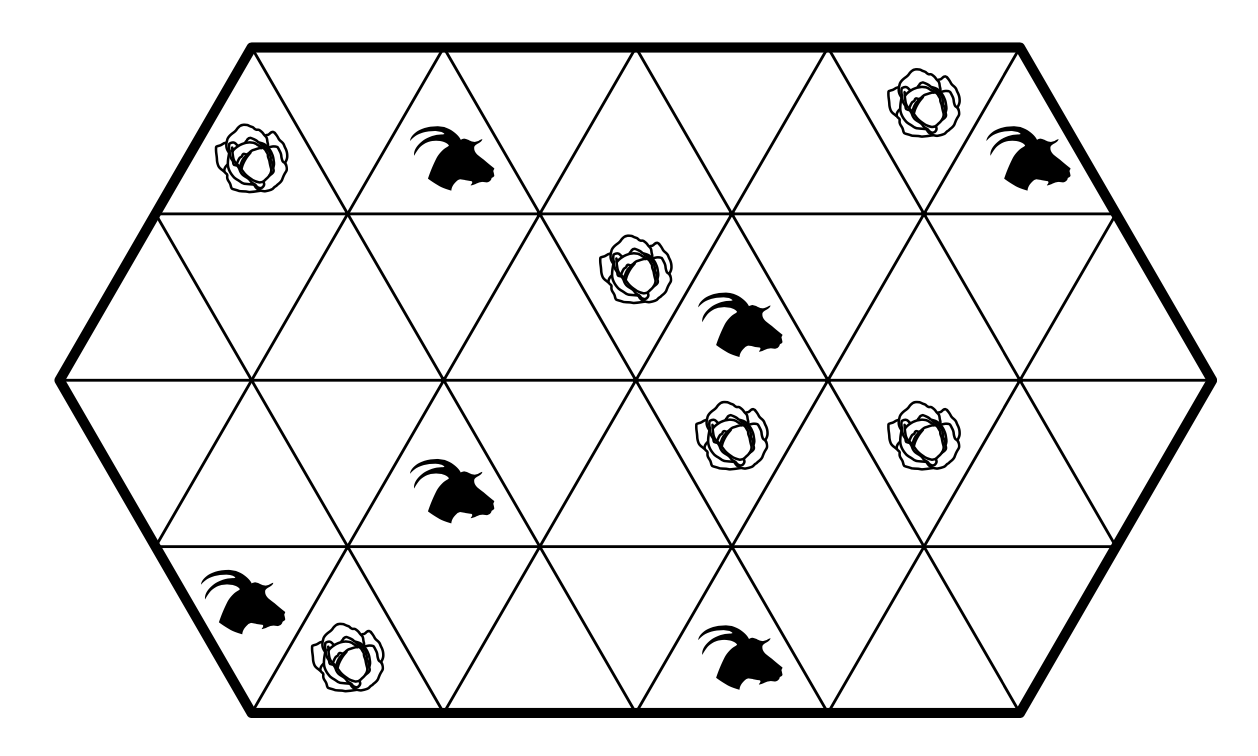
- یک کشاورز دور زمینش را حصار کشید و آن را به مثلث‌هایی به ضلع $50$ متر تقسیم کرد. در برخی از مثلث‌ها کلم کاشت و برخی دیگر را برای چراگاه بزها درنظر گرفت. به کشاورز کمک کنید تا حصارهای اضافی را در امتداد خطوط شبکه با کوتاهترین طول ممکن بسازد تا از همه کلم‌ها در برابر بزها محافظت کند.
- چهار رقم مختلف روی دو کارت، در هر طرف از هر کارت یک رقم، نوشته شده است. آیا ممکن است هر عدد دو رقمی را که می‌توان با این دو کارت ساخت، اول باشد؟
- در بین همه وجه‌های هشت مکعب هم‌اندازه، یک‌سوم وجه‌ها آبی و بقیه قرمز شده‌اند. به کمک این مکعب‌ها یک مکعب بزرگ ساخته‌ایم. یک‌سوم سطح خارجی این مکعب به رنگ قرمز است. نشان دهید به کمک هشت مکعب می‌توانیم مکعبی بسازیم که همه سطح خارجی آن به رنگ قرمز باشد.
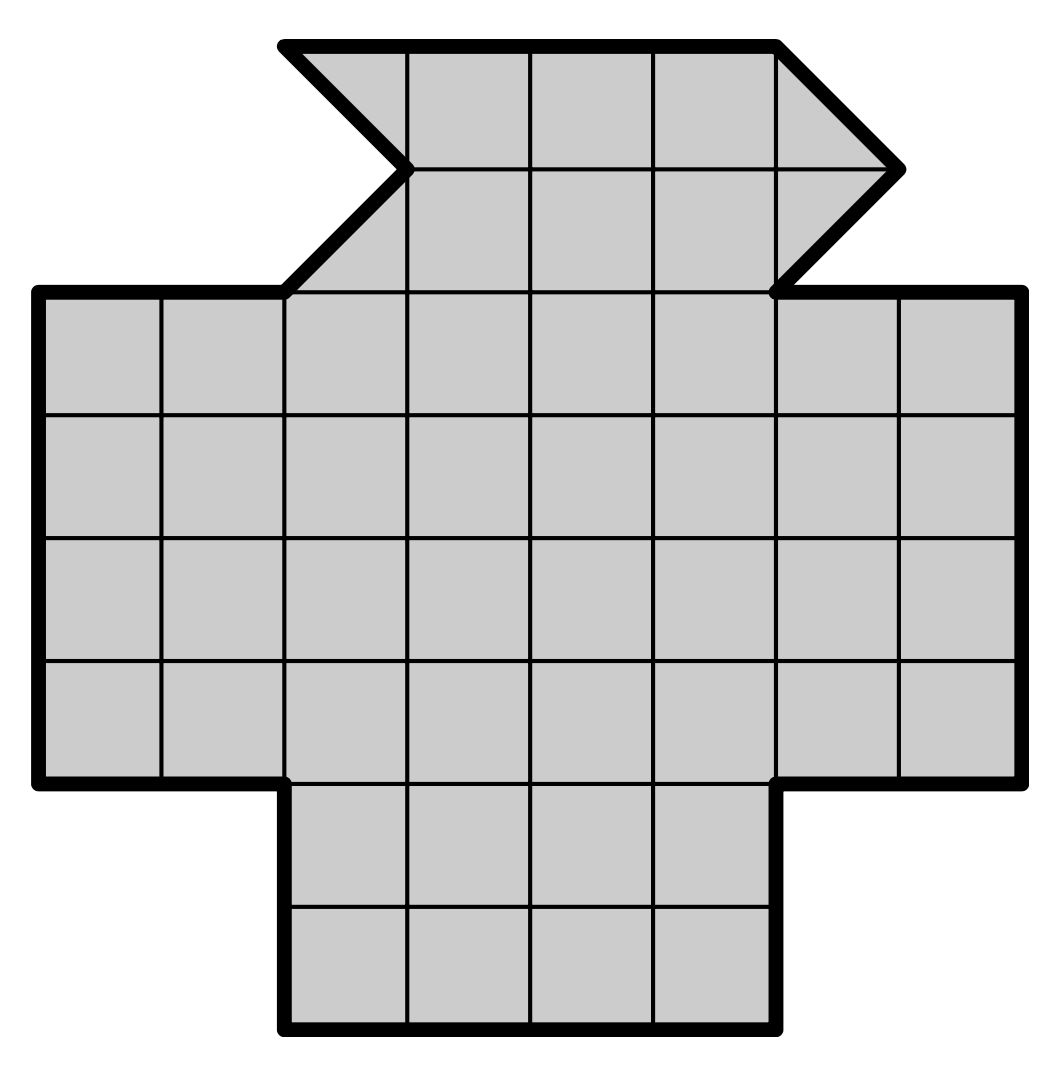
- شکل زیر را به $12$ قسمت برابر تقسیم کنید.
- $100$ عدد ناصفر دور یک دایره نوشته شده‌اند. بین هر دو عدد مجاور، حاصل‌ضرب این دو عدد را یادداشت کرده‌ایم و اعداد اولیه را پاک می‌کنیم. فرض کنید تعداد عددهای مثبت تغییری نکند. در حالت اولیه حداقل چندتا از عددها مثبت هستند؟
- یک ملخ می‌تواند در خانه‌های یک جدول $1\times n$ پرش کند. او در هر حرکت می‌تواند به اندازهٔ $8$، $9$ یا $10$ خانه در هر یک از دو جهت بپرد. می‌گوییم عدد طبیعی $n$ خوب است اگر ملخ بتواند با شروع حرکت از یک خانه از جدول $1\times n$ به هر خانه از جدول دقیقاً یک بار برود. ثابت کنید عدد خوب $n$ بزرگتر از $50$ وجود دارد.
- در مورد هر یک از شکل‌های زیر بگویید که آیا می‌توان اعداد $1$ تا $8$ را در خانه‌های آن قرار داد به‌گونه‌ای که به هر صورتی شکل را به دو قسمت تقسیم کنیم، مجموع اعداد در یکی از دو قسمت بر مجموع اعداد در قسمت دیگر بخش‌پذیر باشد؟
- در یک کلاس $49$ نفره هر کسی حداقل با $25$ نفر دوست است. ثابت کنید این افراد را می‌توان به گروه‌های $2$ و $3$ نفره تقسیم کرد به‌گونه‌ای که در هر گروه هر کسی با بقیه افراد گروه دوست باشد.
- اگر دو بسته کلوچه را بین تعدادی گردشگر به‌طور مساوی پخش کنیم یک کلوچه باقی می‌ماند و اگر سه بسته کلوچه را تقسیم کنیم $13$ کلوچه باقی می‌ماند. تعداد گردشگرها را پیدا کنید.
- داروسازی سه وزنه دارد که به کمک آنها می‌تواند برای مشتری‌های خود $100$ گرم یُد، یا $101$ گرم عسل، یا $102$ گرم پراکسید هیدروژن وزن کند. او همیشه وزنه‌ها را روی یک کفه ترازو قرار می‌دهد و اجناس را روی کفه دیگر. آیا ممکن است هر سه وزنه کمتر از $90$ گرم وزن داشته باشند؟
- مربع $ABCD$ داده شده است. در امتداد قطر $AC$ از سمت $C$ نقطهٔ $K$ قرار دارد به‌گونه‌ای که $BK=AC$. اندازهٔ زاویهٔ $BKC$ را تعیین کنید.
- در عبارت $AB^C =DE^F$ به‌جای هر حرف یکی از رقم‌های $1$ تا $6$ را قرار دهید به‌گونه‌ای که تساوی برقرار باشد. هر یک از رقم‌های $1$ تا $6$ باید در این عبارت ظاهر شوند و در ضمن منظور از عبارت $AB^C$ عدد دو رقمی با رقم‌های $A$ و $B$ است که به توان $C$ رسیده است.
