دانشآموزان عزیز میتوانند با حل این مسائل میزان توانایی خود را در مباحث فصل ۲ ریاضی دهم بسنجند.
معلمهای عزیز میتوانند از این مسائل در کلاس درس یا آزمونها استفاده کنند.
تعداد این مسائل، بهمرور افزایش مییابد.
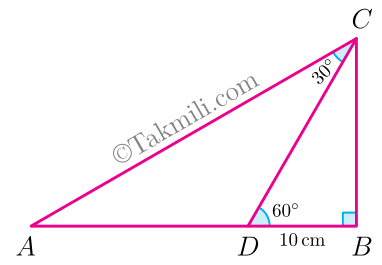
- در مثلث \(ABC\)، زاویهٔ \(B\) قائمه است و نقطهٔ \(D\) روی ضلع \(AB\) قرار دارد. اگر اندازهٔ زاویههای \(BDC\) و \(ACD\) بهترتیب \(60\) و \(30\) درجه و طول \(BD\) برابر \(10\) سانتیمتر باشد، آنگاه طول \(AD\) چقدر است؟
ابتدا شکل مناسبی برای این مسئله رسم میکنیم.

\(BC=10\sqrt{3}\).
در مثلث قائمالزاویهٔ \(BCD\) داریم:
\[\begin{aligned}&\tan 60^{\circ}=\frac{BC}{DB}\\[7pt]&\Rightarrow \sqrt{3}=\frac{BC}{10} \\[7pt]&\Rightarrow BC=10\sqrt{3}.\end{aligned}\]\(\widehat{A}=30^\circ\).
با استفاده از قضیهٔ زاویهٔ خارجی مثلث (در مثلث \(ACD\))، داریم:
\[\begin{aligned}&\widehat{A}+A\widehat{C}D=B\widehat{D}C\\&\Rightarrow\widehat{A}+30^\circ=60^\circ\\&\Rightarrow\widehat{A}=30^\circ.\end{aligned}\]در نتیجه، \(AB=30\,\rm cm\).
در مثلث قائمالزاویهٔ \(ABC\) داریم:
\[\begin{aligned}&\tan\widehat{A}=\frac{BC}{AB}\\[7pt]&\Rightarrow \frac{\sqrt{3}}{3}=\frac{10\sqrt{3}}{AB}\\[7pt]&\Rightarrow AB=30.\end{aligned}\]

بنابراین،
\[\begin{aligned}AD&=AB-BD\\&=30-10\\&=20.\end{aligned}\] - در شکل زیر، فرض کنید که \(AB\) عرشهٔ یک قایق بادبانی بهطول \(8\) متر، و \(FM\) دکل آن باشد. طنابی با زاویه \(60\) درجه از \(A\) به \(M\) (بالای دکل) کشیده شده است. تعداد بیشتری طناب با زاویه \(\theta\) از \(B\) به نقطهٔ \(P\) وصل شده است. اگر نقطهٔ \(P\) دو متر پایینتر از \(M\) باشد، آنگاه مقدار \(MF\) (ارتفاع دکل) را برحسب \(\theta\) بیابید.
- با توجه به شکل زیر، دو تپه در نقطه \(O\) به یکدیگر رسیدهاند. یک تپه با افق زاویه \(30^\circ\) و دیگری زاویه \(45^\circ\) میسازد. نقاط \(A\) و \(B\) روی تپه ها قرار دارند بهطوریکه \(OA=OB=20{\rm m}\).

ستونهای عمودی \(AC\) و \(BD\) با کابل \(CD\) متصل شده اند. اگر \(AC=6{\rm m}\)، و \(CD\) کمترین طول را داشته باشد، اندازه \(BD\) را بیابید. - مطابق شکل زیر، متحرکی ازنقطهٔ \(A\) شروع به حرکت میکند و پس از طی مسافت \(5\sqrt{2}\) کیلومتر به نقطهٔ \(B\) و پس از طی مسافت \(4\sqrt{3}\) به نقطهٔ \(C\) میرسد. جابهجایی کل این متحرک در راستای افقی و در راستای عمودی را بیابید.
- اگر \(\cos \theta=\tan\theta\)، آنگاه مقدارهای ممکن برای \(\sin\theta\) را بهدست آورید.
- اگر \(x\) یک زاویه تند باشد و \(\tan x=\frac{3}{4}\)، حاصل عبارت زیر را بیابید.
\[\frac{\sin x+\cos x-\tan x}{\frac{1}{\cos x}+\cos x-\cot x}\] - در چهارضلعی محدب \(ABCD\)، \(A\widehat{B}C=90^\circ\)، \(B\widehat{C}D=60^\circ\)، و
\[AB=BC=CD=6.\] طول \(AD\) را بیابید. - حاصل عبارت زیر را بهدست آورید.
\[\tan 1^{\circ}\times\tan 2^{\circ}\times\dots\times \tan 88^{\circ}\times\tan 89^{\circ}\] - حاصل عبارت زیر را بیابید.
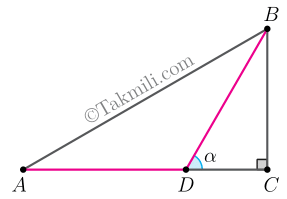
\[\sin^21^\circ+\sin^22^\circ+\dots+\sin^288^\circ+\sin^289^\circ\] - الف) در شکل زیر، \(AD=BD\). ثابت کنید \(\tan\frac{\alpha}{2}=\frac{\sin\alpha}{1+\cos\alpha}\).

ب) مقدار \(\tan15^\circ\) را بهدست آورید. - فرض کنید \(\cos\theta=\frac{m}{m+2}\) و \(\tan\theta=\frac{m+1}{m}\). مقدار عددی \(\sin\theta\) و \(\cot\theta\) را بیابید.
- نیمدایرهای به قطر \(AB\) داده شده است. مماس در نقطه \(B\) را براین نیمدایره رسم میکنیم و از نقطه \(A\) قاطعی میکشیم تا نیمدایره را در \(C\) و مماس رسم شده را در \(D\) قطع کند. اگر \(\alpha\) زاویه بین قاطع و قطر \(AB\)، و \(AD=4AC\)، آنگاه اندازهٔ \(\alpha\) چقدر است؟
- اگر \(\tan x+\cot x>0\)، آنگاه انتهای کمان \(x\) در کدام ناحیهٔ دایره مثلثاتی قرار دارد؟
- اگر \(\sin \alpha\times\cos\alpha < 0\) و \(\sin\alpha-\cos\alpha < 0\)، آنگاه انتهای کمان \(\alpha\) در کدام ناحیه قرار دارد؟
- اگر \(\sin^4 x\times\cos x < 0\) و \(\tan x > \sin x\)، آنگاه انتهای کمان \(x\) در کدام ناحیه قرار دارد؟
- اگر \(180^{\circ}<\alpha<270^{\circ}\)، حاصل عبارت \(A=\sqrt{1-2\sin\alpha\sqrt{1-\sin^2\alpha}}\) را به سادهترین صورت ممکن بنویسید.
- اگر \(\sin x>\sin^3 x\) و \(\cos x<\cos^3 x\)، دراینصورت انتهای کمان \(x\) در کدام ناحیه قرار دارد؟
- میدانیم \(180^\circ <\alpha <360^\circ\). حاصل عبارت زیر را به ساده ترین صورت بنویسید.
\[A=\sin\alpha-\sqrt{\cot^2\alpha-\cos^2\alpha}.\] - اگر \(135^{\circ}<\theta<180^\circ\) باشد، حاصل عبارت زیر را بیابید.
\[A=\sqrt{1-2\sin\theta\cos\theta}-\sqrt[6]{(1+2\sin\theta\cos\theta)^3}\] - اگر \(270^\circ<x<360^\circ\) باشد، حاصل عبارت زیر را بیابید.
\[A=\sqrt[3]{(\tan x+\cot x)^3}+\sqrt[4]{(\sin x+\tan x)^4}+\sqrt{(\cos x-\cot x)^2}\] - اگر \(\sin\alpha\times\sqrt{1-\cot\alpha}>0\) باشد، حدود \(\alpha\) را بیابید.
- اگر \(\sin x\times\cos x < 0\) و \(\sin x+\cos x <0\)، آنگاه انتهای کمان \(x\) در چه بازهای قرار دارد؟
- اگر \(A=2\sin x-1\)، محدوده \(A\) را بیابید.
- اگر \(A=2\cos^3x+3\)، محدوده \(A\) را بیابید.
- محدوده تغییرات \(A=3\sin^4 x-1\) را بیابید.
- محدوده تغییرات \(A=\sin^2 x-4\sin x\) را بیابید.
- اگر \(A=2\cos^2 x-\sin^2x\)، محدوده تغییرات \(A\) را بیابید.
- محدوده تغییرات عبارت \(A=\dfrac{\sin x-1}{\sin x+2}\) را بیابید.
- اگر \(\sin x>\frac{1}{2}\) باشد، \(x\) در چه ناحیهای تغییر میکند؟ (روی دایره مثلثاتی نمایش داده شود.)
- اگر \(\cos x=1-m\) و \(-60^\circ\leq x<60^\circ\)، آنگاه محدوده \(m\) را بیابید.

فرض کنید \(AF=x\). در اینصورت \(MF=\sqrt{3}x\).
\[\begin{aligned}&\tan 60^{\circ}=\frac{MF}{AF}\\[7pt]&\Rightarrow \sqrt{3}=\frac{MF}{x}\\[7pt]&\Rightarrow MF=\sqrt{3}x.\end{aligned}\]
و \(PF=\sqrt{3}x-2\) زیرا
\[\begin{aligned}&PF=MF-MP\\&=\sqrt{3}x-2.\end{aligned}\]
بنابراین، \(x=\dfrac{8\tan\theta+2}{\sqrt{3}+\tan\theta}\).
\[\begin{aligned}& \tan\theta=\frac{PF}{FB}\\[7pt]&\Rightarrow \tan\theta=\frac{\sqrt{3}x-2}{8-x}\\[7pt]&\Rightarrow 8\tan\theta-x\times\tan\theta=\sqrt{3}x-2 \\[7pt]&\Rightarrow 8\tan\theta+2=\sqrt{3}{\color{red}x}+\tan\theta\times{\color{red}x}\\[7pt]&\Rightarrow 8\tan\theta+2=(\sqrt{3}+\tan\theta){\color{red}x}\\[7pt]&\Rightarrow\frac{8\tan\theta+2}{\sqrt{3}+\tan\theta}={\color{red}x}.\end{aligned}\]
و میدانیم \(MF=\sqrt{3}x\) پس \(MF=\dfrac{8\sqrt{3}\tan\theta+2\sqrt{3}}{\sqrt{3}+\tan\theta}\).
با توجه به فرض مسئله، \(CD\) باید بر \(BD\) عمود باشد.

پس شکل مسئله باید بهصورت زیر باشد.

دو ستون \(AC\) و \(BD\) را امتداد میدهیم تا افق را بهترتیب در نقاط \(P\) و \(Q\) قطع کنند.
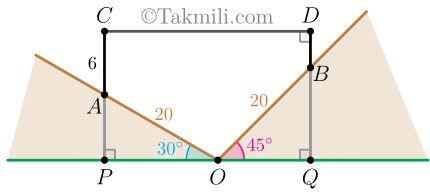
در اینصورت \(CP=16\).
\[\begin{aligned}&\sin30^\circ=\frac{AP}{AO}\\[7pt]&\Rightarrow\frac{1}{2}=\frac{AP}{20}\\[7pt]&\Rightarrow10=AP.\end{aligned}\]بنابراین:
\[\begin{aligned}CP&=AP+AC\\&=10+6\\&=16.\end{aligned}\]
و \(BQ=10\sqrt{2}\).
\[\begin{aligned}&\sin45^\circ=\frac{BQ}{BO}\\[7pt]&\Rightarrow\frac{\sqrt{2}}{2}=\frac{BQ}{20}\\[7pt]&\Rightarrow10\sqrt{2}=BQ.\end{aligned}\]

حال، چون چهارضلعی \(CDQP\) مستطیل است(؟)، پس
\[\begin{aligned}&DQ=CP\\&\Rightarrow BD+BQ=16\\&\Rightarrow BD+10\sqrt{2}=16\\&\Rightarrow BD=16-10\sqrt{2}.\\&\end{aligned}\]

ابتدا از نقطهٔ \(B\) عمودی بر محور \(x\)ها رسم میکنیم و پای عمود را \(H\) مینامیم. سپس، از نقطههای \(A\) و \(C\) عمودهایی بر \(BH\) رسم میکنیم و پای این عمودها را بهترتیب \(M\) و \(K\) مینامیم.
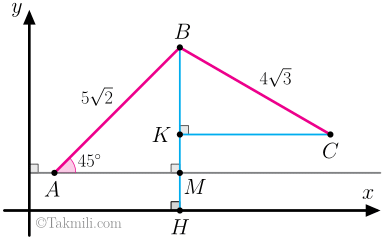
در اینصورت داریم \(AM=5\) و \(CK=6\).
\[\begin{aligned}&\cos 45^\circ =\frac{AM}{AB} \\[7pt]& \Rightarrow AM=AB\times\sin 45^\circ \\& \Rightarrow AM=5\sqrt{2}\times\frac{\sqrt{2}}{2}\\[7pt]&\Rightarrow AM=5.\end{aligned}\]
\(M\widehat{B}C=60^\circ\).
\[\begin{aligned}M\widehat{B}C&=A\widehat{B}C-A\widehat{B}M\\[7pt]&=105^\circ-45^\circ\\[7pt]&=60^\circ.\end{aligned}\]

در مثلث \(BCK\)، داریم:
\[\begin{aligned}&\sin 60^\circ =\frac{CK}{BC}\\[7pt]&\Rightarrow \frac{\sqrt{3}}{2}=\frac{CK}{4\sqrt{3}}\\[7pt]& \Rightarrow \frac{\sqrt{3}}{2}\times4\sqrt{3}=CK\\[7pt]&\Rightarrow6=CK.\end{aligned}\]
پس جابهجایی افقی این متحرک برابر است با:
\[\begin{aligned}AM+CK&=5+6\\&=11.\end{aligned}\]
در ادامه، جابهجایی کل این متحرک در راستای عمودی را محاسبه میکنیم.
بهسادگی میتوان نشان داد که \(BM=5\) و \(BK=2\sqrt{3}\).
\[BM=AM=5.\]

از طرفی، در مثلث \(BKC\) داریم:
\[\begin{aligned}&\cos60^{\circ}=\frac{BK}{BC}\\[7pt]&\Rightarrow \frac{1}{2}=\frac{BK}{4\sqrt{3}}\\[7pt]&\Rightarrow 2\sqrt{3}=BK.\end{aligned}\]
بنابراین، جابجایی کل متحرک در راستای عمودی برابر است با:
\[\begin{aligned}KM&=BM-BK\\&=5-2\sqrt{3}.\end{aligned}\]
از \(\cos \theta=\tan\theta\) میتوان نتیجه گرفت که \(\sin^2 \theta+\sin\theta-1=0\).
\[\begin{aligned}&\cos\theta=\tan\theta\\&\Rightarrow \cos\theta=\frac{\sin\theta}{\cos\theta}\\&\Rightarrow \cos^2 \theta=\sin\theta\\& \Rightarrow 1-\sin^2 \theta=\sin\theta \\& \Rightarrow \sin^2 \theta+\sin\theta-1=0 \end{aligned}\]
بنابراین، \(\sin\theta=\dfrac{-1+\sqrt{5}}{2}\).
\[\begin{aligned}&\sin^2\theta+\sin\theta-1=0\\&\sin^2\theta+\sin\theta=1\\[7pt]&\Rightarrow \sin^2\theta+\sin\theta+{\color{red}\frac{1}{4}}=1+{\color{red}\frac{1}{4}}\\[7pt]&\Rightarrow \big(\sin\theta+\frac{1}{2}\big)^2=\frac{5}{4}\\[7pt]& \Rightarrow \sin \theta+\frac{1}{2}=\pm\frac{\sqrt{5}}{2}\\[7pt]& \Rightarrow \sin\theta=\frac{-1\pm\sqrt{5}}{2}.\end{aligned}\]
چون محدوده تغییرات \(\sin\theta\) بازهٔ \([-1,1]\) است و
\[\frac{-1-\sqrt{5}}{2}\approx-1.65 < -1\] پس \(\sin\theta=\dfrac{-1-\sqrt{5}}{2}\) غیرقابل قبول است. بنابراین: \[\sin\theta=\dfrac{-1+\sqrt{5}}{2}.\]
چون \(x\) یک زاویهٔ تند است و \(\tan x=\frac{3}{4}\)، پس
\[\begin{aligned}\cot x&=\frac{4}{3}\\[7pt]\cos x&=\frac{4}{5}\\[7pt]\sin x&=\frac{3}{5}.\end{aligned}\]
\(\bullet\) با استفاده از اتحاد \(\cot x=\frac{1}{\tan x}\) داریم:
\[\begin{aligned}\cot x&=\frac{1}{\tan x}\\[9pt]&=\frac{1}{\frac{3}{4}}\\[9pt]&=\frac{4}{3}.\end{aligned}\]
\(\bullet\) با استفاده از اتحاد \(\tan^2x+1=\frac{1}{\cos^2x}\) داریم:
\[\begin{aligned}&\tan^2x+1=\frac{1}{\cos^2x}\\[8pt]&\Rightarrow\Big(\frac{3}{4}\Big)^2+1=\frac{1}{\cos^2x}\\[8pt]&\Rightarrow\frac{9}{16}+1=\frac{1}{\cos^2x}\\[8pt]&\Rightarrow\frac{25}{16}=\frac{1}{\cos^2x}\\[8pt]&\Rightarrow\frac{16}{25}=\cos^2x\\[8pt]&\Rightarrow\frac{4}{5}=\cos x.\end{aligned}\]
\(\bullet\) با استفاده از اتحاد \(\sin^2x+\cos^2x=1\) داریم:
\[\begin{aligned}&\sin^2x+\cos^2x=1\\[7pt]&\Rightarrow\sin^2x+\Big(\frac{4}{5}\Big)^2=1\\[7pt]&\Rightarrow\sin^2x+\frac{16}{25}=1\\[7pt]&\Rightarrow\sin^2x=\frac{9}{25}\\[7pt]&\Rightarrow\sin x=\frac{3}{5}.\end{aligned}\]
حال، با جایگذاری مقدارهای بالا در عبارت داده شده، حاصل آن را بهدست میآوریم:
\[\begin{aligned}&\frac{\sin x+\cos x-\tan x}{\frac{1}{\cos x}+\cos x-\cot x}\\[9pt]&=\frac{\frac{3}{5}+\frac{4}{5}-\frac{3}{4}}{\frac{1}{\frac{4}{5}}+\frac{4}{5}-\frac{4}{3}}\\[9pt]&=\frac{\frac{3}{5}+\frac{4}{5}-\frac{3}{4}}{\frac{5}{4}+\frac{4}{5}-\frac{4}{3}}\\[9pt]&=\frac{\frac{12}{20}+\frac{16}{20}-\frac{15}{20}}{\frac{75}{60}+\frac{48}{60}-\frac{80}{60}}\\[9pt]&=\frac{\frac{13}{20}}{\frac{43}{60}}\\[9pt]&=\frac{13}{20}\times\frac{60}{43}\\[9pt]&=\frac{39}{43}.\end{aligned}\]
ابتدا از \(D\) خطی بر \(BC\) عمود میکنیم و پای عمود را \(E\) مینامیم.

در اینصورت داریم:
\[\begin{aligned}&BE=CE=3\quad(1)\\&DE=3\sqrt{3}.\quad(2)\end{aligned}\]
\[\begin{aligned}&\cos 60^\circ=\frac{CE}{CD}\\[7pt]&\Rightarrow CE=CD\times\cos 60^\circ\\&\Rightarrow CE=6\times\frac{1}{2}\\&\Rightarrow CE=3.\end{aligned}\]
از طرفی، چون بنابه فرض مسئله، \(BC=6\)، پس داریم:
\[\begin{aligned}BE&=BC-CE\\&=6-3\\&=3.\end{aligned}\]
همچنین، در مثلث \(CDE\) داریم:
\[\begin{aligned}&\sin60^\circ=\frac{DE}{CD}\\[7pt]&\Rightarrow DE=CD\times\sin 60^\circ\\&\Rightarrow DE=6\times\frac{\sqrt{3}}{2}\\&\Rightarrow DE=3\sqrt{3}.\end{aligned}\]
سپس، از \(D\) خطی بر \(AB\) عمود میکنیم و پای عمود را \(F\) مینامیم.

در اینصورت داریم:
\[\begin{aligned}&DF=3\quad(3)\\&AF=6-3\sqrt{3}.\quad(4)\end{aligned}\]
\[\begin{aligned}&DF=BE=3\\&BF=DE=3\sqrt{3}.\end{aligned}\]

از طرفی، چون بنابه فرض مسئله، \(AB=6\)، پس
\[\begin{aligned}AF&=AB-BF\\&=6-3\sqrt{3}.\end{aligned}\]
در نتیجه، \(AD=6\sqrt{2-\sqrt{3}}\).

با استفاده از قضیهٔ فیثاغورس (در مثلث \(AFD\))، و رابطههای \((3)\) و \((4)\) داریم:
\[\begin{aligned}&AD^2=AF^2+DF^2\\&\Rightarrow AD^2=\big(6-3\sqrt{3}\big)^2+3^2\\&\Rightarrow AD^2=36-36\sqrt{3}+27+9\\& \Rightarrow AD^2=72-36\sqrt{3}\\& \Rightarrow AD^2=36\big(2-\sqrt{3}\big)\\&\Rightarrow AD=\sqrt{36\big(2-\sqrt{3}\big)}\\& \Rightarrow AD=6\sqrt{2-\sqrt{3}}.\end{aligned}\]
پرسش. آیا در این مسئله، میتوان اندازهٔ زاویههای \(CDA\) و \(DAB\) را بهدست آورد؟
برای زاویهٔ \(x\) که \(0^\circ\leq x\leq90^\circ\)، داریم \(\tan x=\cot\big(90^\circ-x\big)\) (؟). بنابراین،
\[\begin{aligned}\tan46^{\circ}&=\cot44^{\circ}\\\tan47^{\circ}&=\cot43^{\circ}\\&\vdots\\\tan88^{\circ}&=\cot2^{\circ}\\\tan89^\circ&=\cot1^\circ.\end{aligned}\quad(1)\]از طرفی، برای هر زاویه دلخواه \(x\) داریم:
\[\tan x\times\cot x=1.\quad(2)\]حال، با استفاده از رابطههای \((1)\) و \((2)\) میتوان حاصل عبارت داده شده را به دست آورد.
\[\tan1^\circ\times\tan2^\circ\times\dots\times\tan88^\circ\times\tan89^\circ=1.\]
احتمالاً شما ایدهٔ گاوس را در مسائل مختلفی دیدهاید. برای حل این مسئله نیز، از ایدهٔ گاوس استفاده شده است.

برای زاویهٔ \(x\) که \(0^\circ\leq x\leq90^\circ\)، داریم \(\sin x=\cos\big(90^\circ-x\big)\) (؟). بنابراین،
\[\begin{aligned}\sin46^{\circ}&=\cos44^{\circ}\\\sin47^{\circ}&=\cos43^{\circ}\\&\vdots\\\sin88^{\circ}&=\cos2^{\circ}\\\sin89^\circ&=\cos1^\circ.\end{aligned}\quad(1)\]از طرفی، برای هر زاویه دلخواه \(x\) داریم:
\[\sin^2x+\cos^2x=1.\quad(2)\]
حال، با استفاده از رابطههای \((1)\) و \((2)\) میتوان حاصل عبارت داده شده را به دست آورد.
\[\sin^21^\circ+\sin^22^\circ+\dots+\sin^288^\circ+\sin^289^\circ=\frac{89}{2}.\]
احتمالاً شما ایدهٔ گاوس را در مسائل مختلفی دیدهاید. برای حل این مسئله نیز، از ایدهٔ گاوس استفاده شده است.

الف) با توجه به شکل داده شده، داریم: \(\widehat A=\dfrac{\alpha}{2}\).
\[\begin{aligned}&\widehat{A}+D\widehat{B}A=C\widehat{D}B\\&\Rightarrow2\widehat{A}=\alpha\\&\Rightarrow\widehat{A}=\frac{\alpha}{2}.\end{aligned}\]
از طرفی، در مثلث \(BCD\) داریم:
\[\begin{aligned}&\sin\alpha=\frac{BC}{BD}\\&\Rightarrow BC=BD\sin\alpha.\quad (1)\end{aligned}\]و
\[\begin{aligned}&\cos\alpha=\frac{CD}{BD}\\&\Rightarrow CD=BD\cos\alpha.\quad (2)\end{aligned}\]

بنابراین، با استفاده از رابطه های \((1)\) و \((2)\) در مثلث \(ABC\)، داریم:
\[\begin{aligned}&\tan\frac{\alpha}{2}=\frac{BC}{AC}\\[10pt]&\Rightarrow\tan\frac{\alpha}{2}=\frac{BC}{AD+DC}\\[9pt]&\Rightarrow \tan\frac{\alpha}{2}=\frac{BD\sin\alpha}{BD+BD\cos\alpha}\\[10pt]&\Rightarrow\tan\frac{\alpha}{2}=\frac{BD\sin\alpha}{BD(1+\cos\alpha)}\\[10pt]&\Rightarrow\tan\frac{\alpha}{2}=\frac{\sin\alpha}{1+\cos\alpha}.\end{aligned}\]
ب) اگر در رابطهٔ \(\tan\frac{\alpha}{2}=\frac{\sin\alpha}{1+\cos\alpha}\)، قرار دهیم \(\alpha=30^\circ\)، آنگاه داریم:
\[\tan15^\circ=2-\sqrt{3}.\]
\[\begin{aligned}\tan15^\circ&=\frac{\sin30^\circ}{1+\cos30^\circ}\\[8pt]&=\frac{\frac{1}{2}}{1+\frac{\sqrt{3}}{2}}\\[8pt]&=\frac{\frac{1}{2}}{\frac{2+\sqrt{3}}{2}}\\[8pt]&=\frac{1}{2}\times\frac{2}{2+\sqrt{3}}\\[8pt]&=\frac{1}{2+\sqrt{3}}\\[8pt]&=\frac{1}{2+\sqrt{3}}\times\frac{2-\sqrt{3}}{2-\sqrt{3}}\\[8pt]&=\frac{2-\sqrt{3}}{4-3}\\[8pt]&=2-\sqrt{3}.\end{aligned}\]

مقادیر ممکن برای \(m\) برابر \(3\) و \(-1\) است.
\[1+\tan^2\theta=\frac{1}{\cos^2\theta}\]
بنابراین
\[\begin{aligned}&1+\big(\frac{m+1}{m}\big)^2=\big(\frac{m+2}{m}\big)^2\\[7pt]&\Rightarrow1+\frac{m^2+2m+1}{m^2}=\frac{m^2+4m+4}{m^2}\\[7pt]&\Rightarrow\frac{m^2+m^2+2m+1}{m^2}=\frac{m^2+4m+4}{m^2}\\[7pt]&\Rightarrow 2m^2+2m+1=m^2+4m+4\\&\Rightarrow m^2-2m-3=0 \\&\Rightarrow (m-3)(m+1)=0\\&\Rightarrow\left\{\begin{aligned}&m=3\\&m=-1.\end{aligned}\right.\end{aligned}\]
\(\bullet\) اگر \(m=-1\)، آنگاه \(\sin\theta=0\) و کتانژانت زاویهٔ \(\theta\) تعریف نشده است.
\[\begin{aligned}\cos\theta&=\frac{m}{m+2}\\[7pt]&=\frac{-1}{-1+2}\\[7pt]&=\frac{-1}{1}\\[7pt]&=-1.\end{aligned}\]از \(\cos\theta=-1\) نتیجه میشود که \(\sin\theta=0\).(؟)
با جایگذاری \(m=-1\) در رابطهٔ \(\tan\theta=\frac{m+1}{m}\)، داریم:
\[\begin{aligned}\tan\theta&=\frac{m+1}{m}\\[7pt]&=\frac{-1+1}{-1}\\&=0.\end{aligned}\] از \(\tan\theta=0\) نتیجه میشود که \(\cot\theta\) تعریف نشده است.(؟)
\(\bullet\) اگر \(m=3\)، آنگاه:
\[\sin\theta=\frac{4}{5},\cot\theta=\frac{3}{4}.\]
\[\cos\theta=\frac{m}{m+2}=\frac{3}{3+2}=\frac{3}{5}\] و
\[\tan\theta=\frac{m+1}{m}=\frac{3+1}{3}=\frac{4}{3}.\]
چون \(\cos\theta\) و \(\tan\theta\) هردو مثبتاند، پس \(\theta\) در ناحیه اول قرار دارد.
حال، چون میدانیم:
\[\begin{aligned}&\tan\theta\times\cot\theta=1\\[7pt]&\Rightarrow\frac{4}{3}\times\cot\theta=1\\[7pt]&\Rightarrow\cot\theta=\frac{3}{4}.\end{aligned}\]
از طرفی، چون میدانیم:
\[\begin{aligned}&\sin^2\theta=1-\cos^2\theta\\[7pt]& \Rightarrow \sin^2\theta=1-\frac{9}{25} \\[7pt]&\Rightarrow\sin^2\theta=\frac{16}{25}\\[7pt]&\Rightarrow \sin\theta=\pm\frac{4}{5}.\end{aligned}\] اما چون \(\sin\theta\) در ناحیه اول مثبت است، پس مقدار منفی غیرقابل قبول است. بنابراین، \(\sin\theta=\frac{4}{5}\).
ابتدا با توجه به فرضیات مسئله، شکل مناسبی رسم میکنیم.

در شکل بالا، پارهخط \(BC\) را رسم کردهایم. دو مثلثهای \(ABD\) و \(ACB\) متشابه هستند.
بنابه قضیهٔ زاویهٔ محاطی، زاویهٔ روبهرو به قطر برابر \(90\) درجه است. در نتیجه، \(A\widehat{C}B=90^\circ\). بنابراین، مثلث \(ACB\) قائمالزاویه است.
پس دو مثلث \(ABD\) و \(ACD\) در حالت زز متشابهاند. زیرا:
\(\bullet\) زاویههای \(ABD\) و \(ACD\) قائمه هستند.
\(\bullet\) زاویهٔ \(A\) در هر دو مثلث مشترک است.
طول \(AC\) با شعاع دایره برابر است.
\[\begin{aligned}&\frac{AB}{AC}=\frac{AD}{AB}\\[7pt]&\Rightarrow\frac{2r}{AC}=\frac{\color{red}AD}{2r}\\[7pt]&\Rightarrow\frac{2r}{AC}=\frac{\color{red}4AC}{2r}\\[7pt]&\Rightarrow 4AC^2=4r^2\\&\Rightarrow AC=r.\end{aligned}\]
پس در مثلث قائمالزاویه \(ABC\) داریم:
\[\begin{aligned}&\cos\alpha=\frac{AC}{AB}\\[7pt]&\Rightarrow\cos\alpha=\frac{1}{2}\\[7pt]&\Rightarrow \alpha=60^\circ.\end{aligned}\]
یادآوری: علامت نسبتهای مثلثاتی در ناحیههای اول تا چهارم
از فرض \(\tan x+\cot x>0\) نتیجه میشود که \(\tan x\) و \(\cot x\) هر دو مثبتاند.
از طرفی، چون \(\tan x+\cot x>0\)، پس واضح است که مقدارهای \(\tan x\) و \(\cot x\)، هر دو مثبتاند.
میدانیم که در ناحیههای اول و سوم، \(\tan x\) و \(\cot x\) مثبتاند. پس انتهای کمان \(x\) در ناحیهٔ اول یا سوم قرار دارد.
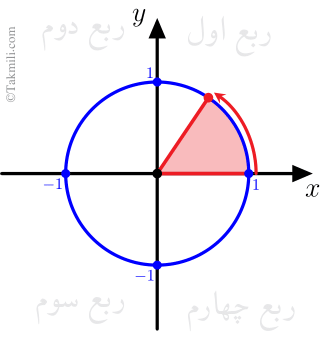
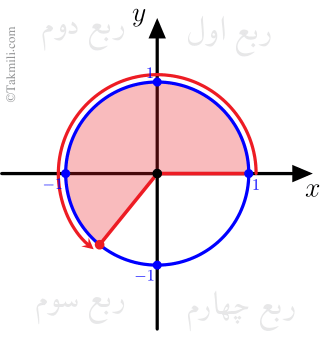
از \(\sin \alpha\times\cos\alpha<0\) نتیجه میشود که انتهای کمان \(\alpha\) در ناحیهٔ دوم یا چهارم قرار دارد.
از \(\sin\alpha-\cos\alpha<0\) نتیجه میشود که \(\alpha\) در ناحیهٔ دوم قرار ندارد.
\[\begin{aligned}&\sin\alpha-\cos\alpha<0\\&\Rightarrow\sin\alpha<\cos\alpha.\quad(*)\end{aligned}\]چون در ناحیهٔ دوم رابطهٔ \((*)\) برقرار نیست(؟)، پس \(\alpha\) نمیتواند در ناحیهٔ دوم باشد.
پس انتهای کمان \(\alpha\) در ناحیهٔ چهارم قرار دارد.
واضح است که \(\sin^4 x\geq0\). پس
\[\begin{aligned}&\overbrace{\sin^4 x}^{\geq0}\times\cos x<0\\&\Rightarrow \cos x <0.\quad(1)\end{aligned}\]
از رابطهٔ \((1)\) و فرض \(\tan x > \sin x\)، میتوان نتیجه گرفت:\[\sin x < 0.\quad(2)\]
حال، میخواهیم علامت کسر \(\frac{1-\cos x}{\cos x}\) را تعیین کنیم.
\(\bullet\) با توجه به رابطهٔ \((1)\)، مخرج کسر \(\frac{1-\cos x}{\cos x}\) منفی است.
\(\bullet\) چون همواره \(\cos x\leq1\)، پس \(0 \leq 1-\cos x\) یا بهطور معادل \(1-\cos x\geq0\). بنابراین، صورت کسر \(\frac{1-\cos x}{\cos x}\)، نامنفی است.
پس، با توجه به رابطهٔ \((2)\) داریم:
\[\begin{aligned}&\sin x\big(\frac{\overbrace{1-\cos x}^{\geq 0}}{\underbrace{\cos x}_{ < 0}}\big) > 0\\[9pt]&\Rightarrow\sin x < 0.\end{aligned}\]
حال، از رابطههای \((1)\) و \((2)\) نتیجه میشود که انتهای کمان \(x\) در ناحیهٔ سوم قرار دارد.

به کمک اتحاد مثلثاتی \(\sin^2\alpha+\cos^2\alpha=1\) داریم:
\[\begin{aligned}A&=\sqrt{1-2\sin\alpha\sqrt{1-\sin^2\alpha}}\\&=\sqrt{1-2\sin\alpha\sqrt{\cos^2\alpha}}\\&=\sqrt{1-2\sin\alpha|\cos\alpha|}\end{aligned}\]
چون انتهای کمان \(\alpha\) در ناحیهٔ سوم قرار دارد، پس \(\cos\alpha<0\). بنابراین، \(|\cos\alpha|=-\cos\alpha\). در نتیجه:
\[\begin{aligned} A&=\sqrt{1-2\sin\alpha|\cos\alpha|}\\&=\sqrt{1-2\sin\alpha(-\cos\alpha)}\\&=\sqrt{{\color{red}1}+2\sin\alpha\cos\alpha} \\&= \sqrt{{\color{red}\sin^2\alpha+\cos^2\alpha}+2\sin\alpha\cos\alpha}\\&=\sqrt{(\cos\alpha+\sin\alpha)^2}\\&=|\cos\alpha +\sin\alpha|\end{aligned}\]
چون \(180^\circ < \alpha < 270^\circ\)، پس
\[\left.\begin{aligned} &\cos\alpha < 0\\ &\sin\alpha < 0\end{aligned}\right\}\Rightarrow\cos\alpha+\sin\alpha < 0.\]
بنابراین:
\[\begin{aligned}A&=|\overbrace{\cos\alpha+\sin\alpha}^{<0}|\\&=-(\cos\alpha+\sin\alpha)\\&=-\cos\alpha-\sin\alpha.\end{aligned}\]
با توجه به \(\sin x>\sin^3 x\)، انتهای زاویهٔ \(x\) در ناحیه اول یا دوم قرار دارد. \((1)\)
با توجه به \(\cos x<\cos^3 x\)، انتهای زاویه \(x\) در ناحیه دوم یا سوم قرار دارد. \((2)\)
با توجه به دو نتیجهٔ \((1)\) و \((2)\)، انتهای کمان \(x\) در ناحیهٔ دوم قرار دارد.
به کمک اتحادهای مثلثاتی\(\cot\alpha=\frac{\cos\alpha}{\sin\alpha}\) و \(\sin^2\alpha+\cos^2\alpha=1\)، میتوان نتیجه گرفت که \(A=\sin\alpha-\frac{|\cos^2\alpha|}{|\sin\alpha|}\) میرسیم.
چون \(\alpha\) در ناحیه سوم و چهارم دایره مثلثاتی قرار دارد، پس \(A= \frac{1}{\sin\alpha}\).
\[\begin{aligned}A&=\sin\alpha-\frac{|\cos^2\alpha|}{|\sin\alpha|}\\[7pt]&=\sin\alpha-\frac{\cos^2\alpha}{-\sin\alpha}\\[7pt]&=\sin\alpha+\frac{\cos^2\alpha}{\sin\alpha}\\[7pt]& =\frac{\sin^2\alpha+\cos^2\alpha}{\sin\alpha}\\[7pt]&=\frac{1}{\sin\alpha}.\end{aligned}\]
با استفاده از اتحاد \(\sin^2\theta+\cos^2\theta=1\) میتوان ثابت کرد:
\[(\sin\theta+\cos\theta)^2=1+2\sin\theta\cos\theta\]
و به طریق مشابه ثابت میشود:
\[(\sin\theta{\color{red}-}\cos\theta)^2=1{\color{red}-}2\sin\theta\cos\theta.\]
بنابراین
\[\begin{aligned}A&=\sqrt{1-2\sin\theta\cos\theta}-\sqrt[6]{(1+2\sin\theta\cos\theta)^3}\\&= \sqrt{(\sin\theta-\cos\theta)^2}-\sqrt[6]{\big((\sin\theta+\cos\theta)^2\big)^3}\\&= \sqrt{(\sin\theta-\cos\theta)^2}-\sqrt[6]{(\sin\theta+\cos\theta)^6}\\&=|\sin\theta-\cos\theta|-|\sin\theta+\cos\theta|\end{aligned}\]
چون \(135^{\circ}<\theta<180^\circ\)، پس \((\sin\theta-\cos\theta)>0\) و \((\sin\theta+\cos\theta)<0\).
میدانیم \(|\sin135^\circ|=|\cos135^\circ|\). از طرفی، همانطور که در ویدئوی بالا میبینید اگر \(135^\circ<\theta<180^\circ\)، آنگاه \(|\sin\theta|<|\cos\theta|\) و در نتیجه:
\[\sin\theta+\cos\theta<0.\]
بنابراین \(A=2\sin\theta\).
\[\begin{aligned}A&=\sqrt[3]{(\tan x+\cot x)^3}+\sqrt[4]{(\sin x+\tan x)^4}+\sqrt{(\cos x-\cot x)^2}\\&=(\tan x+\cot x)+|\sin x+\tan x|+|\cos x-\cot x|.\\\end{aligned}\]
اگر \(270^\circ<x<360^\circ\)، آنگاه \(\sin x+\tan x<0\).
\[\left.\begin{aligned}\sin x<0\\\tan x<0\end{aligned}\right\}\Rightarrow\sin x+\tan x<0.\]
اگر \(270^\circ<x<360^\circ\)، آنگاه \(\cos x-\cot x>0\).
\[\left.\begin{aligned}\cos x>0\\\cot x<0\end{aligned}\right\}\Rightarrow\cos x-\cot x>0.\]
بنابراین:
\[\begin{aligned}A&=(\tan x+\cot x)+|\overbrace{\sin x+\tan x}^{ < 0}|+|\overbrace{\cos x-\cot x}^{ > 0}|\\&=\tan x+\cot x+\big(-(\sin x+\tan x)\big)+\cos x-\cot x\\&=\tan x+\cot x-\sin x-\tan x+\cos x-\cot x\\&=-\sin x+\cos x.\end{aligned}\]
از \(\sin\alpha\times\sqrt{1-\cot\alpha}>0\) میتوان نتیجه گرفت که \(\sin\alpha > \cos\alpha\).
\[\begin{aligned} &\sqrt{1-\cot\alpha} > 0\\&\Rightarrow 1-\cot\alpha > 0\\&\Rightarrow 1 > \cot\alpha\\&\Rightarrow 1 > \frac{\cos\alpha}{\sin\alpha}\\ {\color{red}(\sin\alpha > 0)}\;&\Rightarrow\sin\alpha > \cos\alpha.\end{aligned}\]
در نتیجه: \(45^\circ <\alpha <180^\circ \).
واضح است که
\[90^\circ\leq\alpha\leq180^\circ\Rightarrow\sin\alpha > \cos\alpha.\quad (1)\]
حال باید در ناحیهٔ اول دایرهٔ مثلثاتی، زاویههایی مانند \(\alpha\) را پیدا کنیم که برای آنها \(\sin\alpha > \cos\alpha\).
میدانیم که \(\sin45^\circ=\cos45^\circ\). از طرفی، با توجه به نمودار بالا، واضح است که اگر
\[\begin{aligned}&0\leq\alpha < 45^\circ\Rightarrow\sin\alpha<\cos\alpha\\&45^\circ<\alpha\leq90^\circ\Rightarrow\sin\alpha>\cos\alpha.\quad(2)\end{aligned}\]
اکنون، باتوجه به رابطههای \((1)\) و \((2)\) داریم:
\[45^\circ < \alpha\leq180^\circ.\]
چون \(\sin x\times\cos x < 0\)، پس \(\sin x\) و \(\cos x\) مختلفالعلامت هستند؛ یعنی یکی مثبت و دیگری منفی است. بنابراین، انتهای کمان \(x\) در ناحیهٔ دوم یا چهارم قرار دارد.
از طرفی، میدانیم که \(\sin x+\cos x <0\). در ناحیهٔ دوم \(\sin135^\circ=-\cos135^\circ\) و در ناحیهٔ چهارم \(\sin(315)^\circ=-\cos(315)^\circ\).
حال، با توجه به شکلهای زیر، \(x\) متعلق به بازهٔ \((135^\circ, 180^\circ)\) یا \((270^\circ , 315^\circ)\) است.
با توجه به محدوده تغییرات \(\sin x\)، یعنی \(-1\leq\sin x\leq1\)، محدوده تغییرات \(A\) در بازهٔ \([-3 , 1]\) است.
با توجه به اینکه برای هر زاویهٔ دلخواه، مانند \(x\)، داریم \(-1\leq\cos x\leq 1\)، بنابراین محدوده تغییرات \(A\) در بازه \([1,5]\) قرار دارد.
باتوجه به اینکه برای هر زاویهٔ دلخواه، مانند \(x\)، داریم \(-1\leq\sin x\leq 1\)، بنابراین \(-1\leq A\leq 2\).
\[\begin{aligned}& -1\leq\sin x\leq1\\[7pt]&\Rightarrow 0\leq\sin^4 x\leq 1 \\[7pt]& \Rightarrow 0\leq 3\sin^4 x\leq 3 \\[7pt]&\Rightarrow 0{\color{red}\,-\,1}\leq 3\sin^4 x{\color{red}\,-\,1}\leq 3{\color{red}\,-\,1}\\[7pt]&\Rightarrow -1\leq 3\sin^4 x-1\leq 2\\[7pt]&\Rightarrow -1\leq A\leq 2.\end{aligned}\]
\[\begin{aligned}A&=\sin^2 x-4\sin x{\color{red}\,+\,4\,-\,4}\\&= {\color{blue}(\sin x)^2\,-\,2(\sin x)(2)\,+\,2^2}-4\\&={\color{blue}(\sin x\,-\,2)^2}-4.\end{aligned}\]
بنابراین \(-3\leq A\leq 5\).
ابتدا با استفاده از اتحاد مثلثاتی \(\sin^2x+\cos^2x=1\)، عبارت \(A\) را فقط برحسب \(\cos x\) مینویسیم:
\[\begin{aligned}A&=2\cos^2 x-{\color{red}\sin^2x}\\[7pt]&=2\cos^2x-{\color{red}(1\,-\,\cos^2x)}\\[7pt]&=3\cos^2x-1.\end{aligned}\]
پس \(-1\leq A\leq 2\).
عبارت را طوری تغییر شکل میدهیم که فقط در مخرج نسبت مثلثاتی \(\sin x\) را داشته باشیم:
\[\begin{aligned} A&=\frac{\sin x-1{\color{red}\,+\,2\,-\,2}}{\sin x+2}\\[9pt]&=\frac{\sin x+2-3}{\sin x+2}\\[9pt]&=\frac{\sin x+2}{\sin x+2}-\frac{3}{\sin x+2}\\[9pt]&=1-\frac{3}{\sin x+2}.\end{aligned}\]
حال به کمک محدوده تغییرات \(\sin x\)، میتوان تعیین کرد که برای هر \(x\)، \(\dfrac{3}{\sin x+2}\) در بازه \([1,3]\) قرار میگیرد.
\[\begin{aligned} &-1\leq\sin x\leq1 \\&\Rightarrow 1\leq\sin x+2\leq3\\&\Rightarrow 1\geq\frac{1}{\sin x+2}\geq\frac{1}{3}\\&\Rightarrow 3\geq\frac{3}{\sin x+2}\geq1.\end{aligned}\]
بنابراین \(-2\leq A \leq 0\).
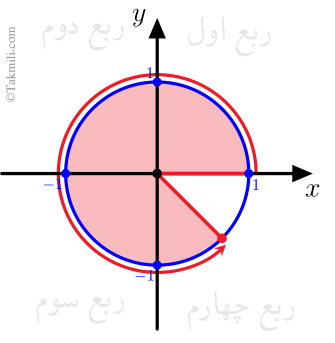
خط \(y=\frac{1}{2}\) را رسم میکنیم تا دایره مثلثاتی را قطع کند.

نقاط تلاقی خط و دایره، مکان زاویههایی است که \(\sin x=\frac{1}{2}\). با توجه به شکل بالا، فقط برای \(30^\circ<x<150^\circ\) داریم \(\sin x>\frac{1}{2}\). بنابراین \(30^\circ<x<150^\circ\).
همانطور که در شکل زیر میبینید، اگر \(-60^\circ<x<60^\circ\)، آنگاه \(\frac{1}{2}\leq\cos x\leq1\) است.
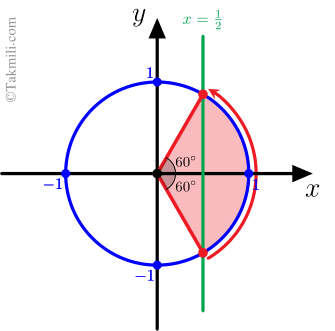
بنابراین:
\[\begin{aligned}&\frac{1}{2}\leq\cos x\leq 1\\&\Rightarrow\frac{1}{2}\leq 1-m\leq 1\\&\Rightarrow \frac{-1}{2}\leq -m\leq 0\\&\Rightarrow \frac{1}{2}\geq m\geq0.\end{aligned}\]



ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️عالی
سلام و عرض ادب
در انتهای سوال 28 اشتباهی در علامت بزرگتر کوچیکتر گذاری رخ داده و برعکس شده
با سلام و احترام
متأسفانه متوجه اشتباه نشدم. لطفاً سطری که در آن اشتباه رخ داده را دقیقتر مشخص کنید.
سپاس از همراهی و توجه شما
در سطر آخر و نتیجه گیری
نوشتید که A کوچکتر از -2 و بزرگتر از 0 است
علامت ها را برعکس گذاشتید
با سپاس فراوان از شما
اصلاح شد.
سلام و احترام
ببخشید در سوال ۵۱ نمی تونستیم از اینکه آلفا بین صفر و ۱۸۰ درجه هست نتیجه بگیریم سینوسش بزرگ تر از صفره؟
سلام
نتیجهگیری شما درست است.
سلام
خسته نباشید
من قسمت آخر سوال ۴۱ رو متوجه نشدم
یعنی قدرمطلق حاصلضرب سینوس در کسینوس زاویه x با قدرمطلق حاصل جمعشون برابره؟
سلام
با عرض پوزش فراوان، متأسفانه در صورت مسئله یک اشتباه تایپی رخ داده بود که اصلاح شد.
سلام و احترام
خسته نباشید
ببخشید در انتهای سوال ۲۸ اشتباهی رخ نداده است؟
سلام و عرض ادب
لطفاً اشتباه مذکور را دقیقتر مشخص کنید.
سپاسگزارم.
با سلام و عرض ادب
در پاسخ به سوال۲۳ یک اشتباهی در جواب نهایی کردید
با سلام و احترام
ممنون که تذکر دادید
اصلاح شد.
سلام خیلی ممنون ازسایت خوبتون اگرممکنه برای سالیازدهم ودوازدهم هم مطلب بزارین چون مطالبتون خیلی مفیده برامون??
در پرسش ابی رنگ 7 باید گفت بله CDA=135 و DAB=75
سلام اگه امکانش هست کمی زودتر درسنامه ها و سوالات دهم و اگه شد یازدهم رو اماده کنین چون اگه با همین سرعت پیش برین ما کنکورمون تموم میشه بعدش شاید برسین به یازدهم و کمی هم دوازدهم این طوری درسته که کیفیت مطالبتون بالاس ولی دیگه بدردمون نمیخوره میگن نوش دارو بعد مرگ سهراب همینه دیگه 🙂
ولی انصافا مطالبتون خیلی مفید و عالین خیلی ممنون از همتون