مسابقه تلویزیونی هوشیار – قسمت ۲۷

با حروف گزینهٔ۱ واژهٔ «احترام»
با حروف گزینهٔ۲ واژهٔ «سرگشته»
با حروف گزینهٔ۳ واژهٔ «خیابان»
با حروف گزینهٔ۴ واژهٔ «پرتوقع» ساخته می‌شود. واژهٔ «سرگشته» مترادف با مدهوش است.

شکل زیر را باید جایگزین کاشی شمارهٔ \(7\) کنیم.

در این‌صورت قاعدهٔ گفته شده برقرار است.

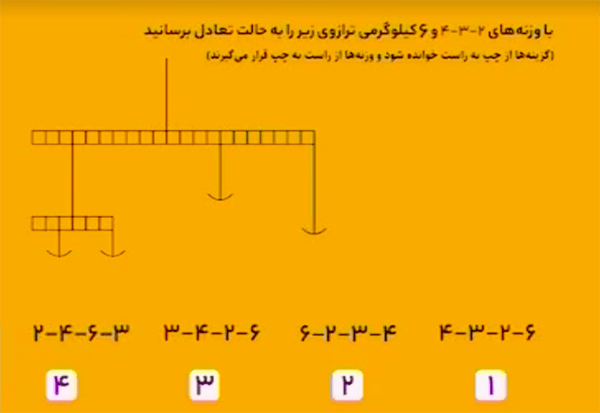
در شکل بالا، قسمت سمت چپ پایین متعادل است. زیرا:
\[6\times{\color{red}1}=2\times{\color{red}3}.\] توجه کنید که اعداد \(1\) و \(3\) در رابطهٔ بالا، فاصلهٔ وزنه‌ها از خط مشخص شده در شکل زیر هستند.

وزن سمت چپ برابر است با:
\[\begin{aligned}&(6+2)\times{\color{red}7}\\&=8\times7\\&=56.\end{aligned}\] توجه کنید که عدد \(7\) در رابطهٔ بالا، فاصلهٔ خط آبی از خط قرمز در شکل زیر است.

و وزن سمت راست برابر است با: \[\begin{aligned}&4\times{\color{red}11}+3\times{\color{red}4}\\&=44+12\\&=56.\end{aligned}\] توجه کنید که اعداد \(11\) و \(4\) فاصله‌ٔ وزنه‌های سمت راست از خط مشخص شده در شکل زیر است.

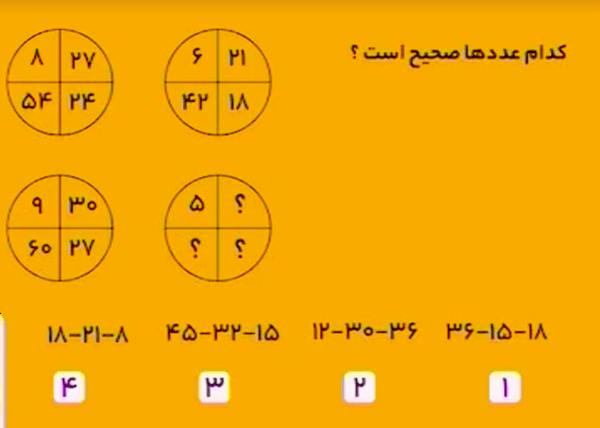
در هر دایره، عدد سمت راست پایینی، سه‌‌برابر عدد سمت چپ بالایی است؛ عدد سمت راست بالایی سه واحد بیشتر از عدد سمت راست پایینی است؛ و عدد سمت چپ پایینی دو برابر عدد سمت راست بالایی است.
پس، به‌جای علامت سؤال، باید اعداد زیر را قرار داد.

هر سطر را یک عدد هفت‌رقمی در نظر بگیرید. در این‌صورت داریم:
\[5749827+3864759=9614586.\] بنابراین، به‌جای علامت سؤال باید عدد \(6\) را قرار دهیم.

سن لقمان یک‌ویک‌سوم سن کیوان است. یعنی سن لقمان
\[1\frac{1}{3}=\frac{4}{3}\] سن کیوان است.
سن هادی یک‌ویک‌سوم سن لقمان است. یعنی سن هادی
\[1\frac{1}{3}=\frac{4}{3}\] سن لقمان، یا \[\frac{4}{3}\times\frac{4}{3}=\frac{16}{9}\] سن کیوان است. بنابراین، نسبت سن کیوان به لقمان \(1\) به \(\frac{4}{3}\) و نسبت سن کیوان به هادی \(1\) به \(\frac{16}{9}\) است. چون
\[\begin{aligned}&1+\frac{4}{3}+\frac{16}{9}\\[7pt]&=\frac{9}{9}+\frac{12}{9}+\frac{16}{9}\\[7pt]&=\frac{37}{9}\end{aligned}\] و \[\frac{74}{\frac{37}{9}}=18\] پس سن کیوان، لقمان، و هادی به‌ترتیب برابر است با:
\[\begin{aligned}&1\times18=18\\[7pt]&\frac{4}{3}\times18=24\\[7pt]&\frac{16}{9}\times18=32.\end{aligned}\]

در همهٔ شکل‌ها، به‌جز شکل زیر، ناحیه‌ٔ مشترک بین دایره، مثلث، و مربع، سیاه شده است.

رقم‌های همهٔ اعداد داده شده، به‌جز \(6957\)، از چپ به راست با روند زیر تولید می‌شوند:
\[+3,-2,+3.\] برای مثال، در عدد \(3647\) داریم:
\[\begin{aligned}&3+3=6\\&6-2=4\\&4+3=7.\end{aligned}\]

حاصل‌جمع اعداد داخل دایره‌های سمت چپ و میانی برابر \(100\) است. پس حاصل‌جمع اعداد داخل دایرهٔ سمت راست نیز باید برابر \(100\) باشد. بنابراین، به‌جای علامت سؤال باید عدد \(13\) را قرار دهیم. زیرا: \[16+71+13=100.\]