مسابقه تلویزیونی هوشیار – قسمت ۲۸

ما این سؤال را به شکل زیر ترجمه کردیم:
مرد شلخته‌ای در کشوی خود \(53\) لنگه جوراب دارد: \(21\) لنگه جوراب آبی، \(15\) لنگه جوراب سیاه، و \(17\) لنگه جوراب قرمز. چراغ‌های اتاق او سوخته‌اند. مرد شلخته در تاریکی حداقل چند لنگه جوراب از کشوی خود بردارد تا صد در صد مطمئن شود که یک جفت جوراب سیاه برداشته است؟

چون مرد شلخته، \(21\) لنگه جوراب آبی و \(17\) لنگه جوراب قرمز دارد، پس اگر او \(21+17=38\) لنگه جوراب بردارد، ممکن است که هیچ لنگه جوراب سیاهی بر نداشته باشد. بنابراین، برای اینکه صد در صد مطمئن شود که حتماً یک جفت جوراب سیاه برداشته است، باید \(38+2=40\) لنگه جوراب برداشته باشد.

پاسخ این سؤال در کتاب اصلی به‌صورت زیر آمده است که البته، غلط است! زیرا اولویت عملگرهای ریاضی در آن رعایت نشده است.

درسنامه اولویت عملگرها

ظاهراً فیلیپ کارتر با اولویت عملگرهای آشنایی نداشته است. چون در چند نمونهٔ دیگر از این سؤالات نیز در کتابش آمده است و او پاسخ آنها را هم همین‌طور غلط نوشته است!
در کتاب ریاضیات تکمیلی هفتم، این‌گونه مسائل اصلاح شده‌اند. برای مشاهدهٔ چند نمونهٔ اصلاح شده از این مسائل، اینجا را کلیک کنید.

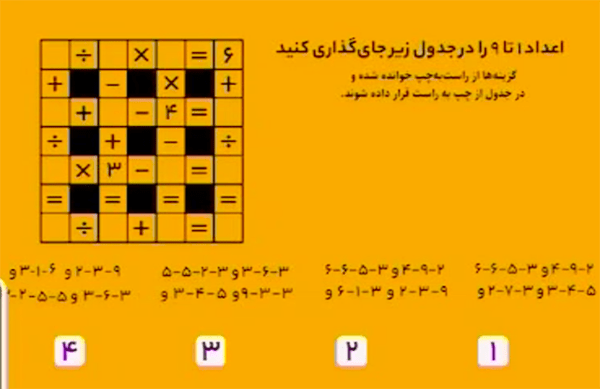
پاسخ، عدد ۱۰ است.
اعداد روی خطوط سبز را جمع بزنید.

\[\begin{aligned}&4\\&2+3=5\\&2+1+3=6\\&2 + 1 + 2 + 2 =7\\& 4+1+3=8\\& 5+4=9\\&10\end{aligned}\]

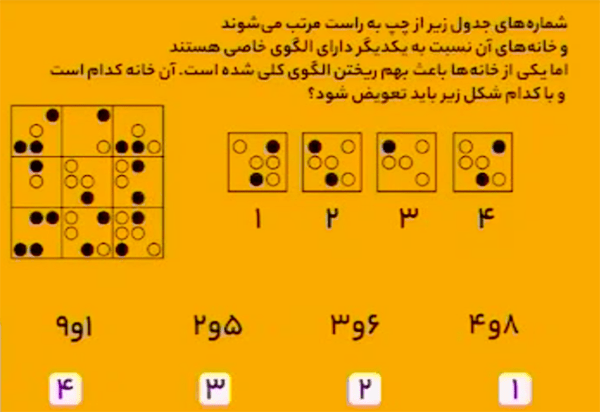
کاشی ۸ باید با کاشی شمارهٔ ۴ جایگزین شود.

توجه کنید که در هر سطر و ستون، کاشی‌های اول و دوم را روی هم قرار می‌دهیم تا کاشی سوم حاصل شود با این شرط که شکل‌هایی که روی می‌افتند حذف می‌شوند.

---

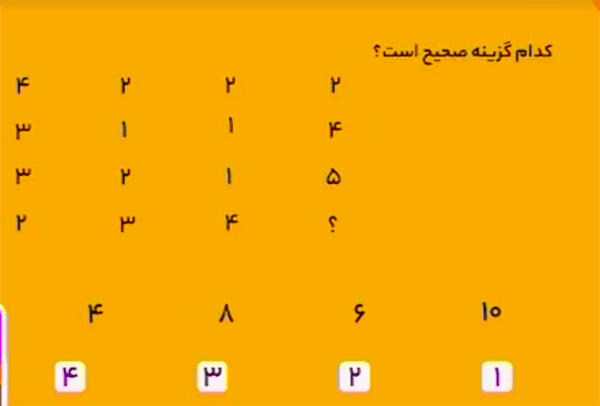
پاسخ، گزینهٔ ۴ است.

در هر سطر شکل داخل مربع دوم (از سمت چپ)، ترکیب شکل‌های داخل مربع‌های اول، سوم، و چهارمِ آن سطر است.

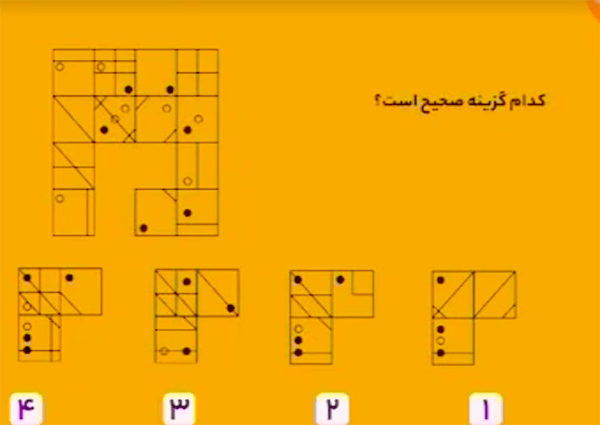
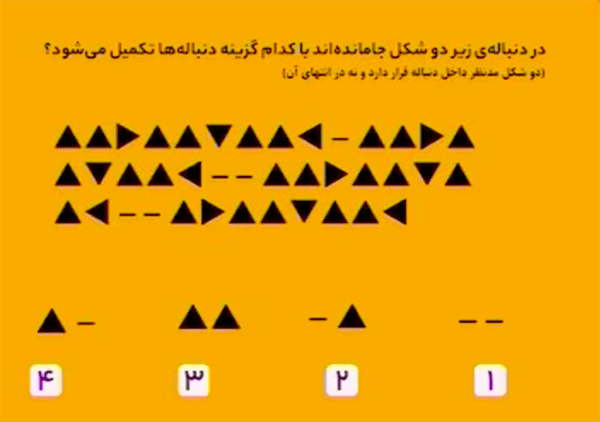
پاسخ، گزینهٔ ۲ است.

در این دنباله، نمادهای داخل کادر قرمز چهار بار آمده‌اند. بین بار اول و دوم یک خط فاصله (-) است. بین بار دوم و سوم دو خط فاصله (- -) و بین بار سوم و چهار باید سه خط فاصله باشد (- – -).

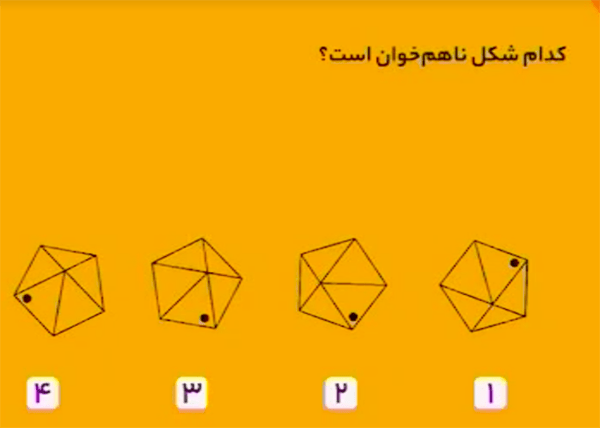
همهٔ شکل‌های داده شده، به‌جز شکل زیر، با دوران (چرخش) به یکدیگر تبدیل می‌شوند.

پاسخ 34826 است.

هر عدد از عدد قبلی ساخته می‌شود؛ با این قانون که مجموع دو رقمِ‌ سمت راستِ عدد قبلی، سمت راستِ عدد جدید نوشته می‌شود و بقیهٔ ارقامِ عدد قبلی، با ترتیب برعکس، سمت چپ عدد جدید قرار می‌گیرد.

برای مثال، عدد 284315 این‌گونه به‌دست آمده است:
مجموع دو رقم سمت راستِ عدد 348269، سمت راستِ عدد 284315 نوشته شده و رقم‌های دیگر عدد 348269 (یعنی 3482)، با ترتیب برعکس (یعنی به‌صورت 2843)، سمت چپ عدد 284315 نوشته شده است.

گزینهٔ۲ صحیح است.

\[(6\times 9)+8=62\]