مسابقه تلویزیونی هوشیار – قسمت ۲۹

در هر سطر، روند تولید هر عدد از عدد قبلی به‌صورت زیر است: \[+2,-3,+2.\]
در هر ستون، روند تولید هر عدد از عدد قبلی به‌‌صورت زیر است: \[-3,+2,-3.\]

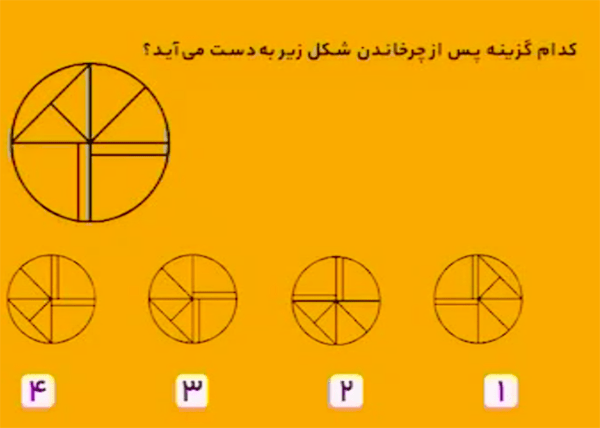
گزینهٔ ۴ صحیح است زیرا، شکل داده شده هفت ضلعی است و در هر مرحله فاصلهٔ بین دایره سیاه و سفید سه ضلع (چهار ضلع) خواهد بود.

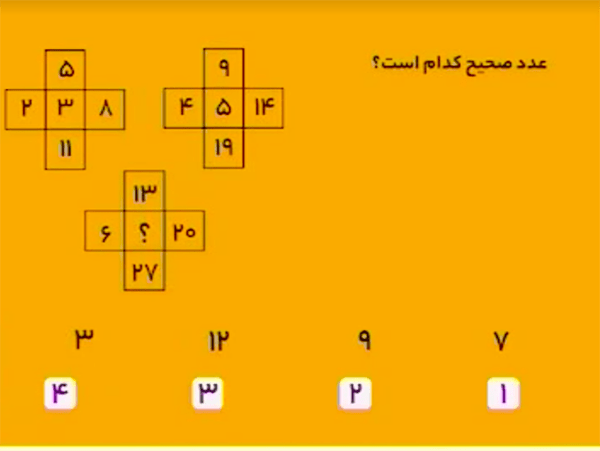
در شکل بالا سمت چپ، اعداد دور \(3\)، با ترتیب زیر، \(3\)تا \(3\)تا اضافه می‌شوند:
\[2,5,8,11.\]
در شکل بالا سمت راست، اعداد دور \(5\)، باترتیب زیر، \(5\)تا \(5\)تا اضافه می‌شوند:
\[4,9,14,19.\]
در شکل پایین، اعداد دور \(?\)، با ترتیب زیر، \(7\)تا \(7\)تا اضافه می‌شوند:
\[6,13,20,27.\]
پس به‌جای علامت سؤال باید عدد \(7\) را قرار داد.

گزینهٔ ۴ صحیح است.

پاسخ، گزینهٔ ۱ است.

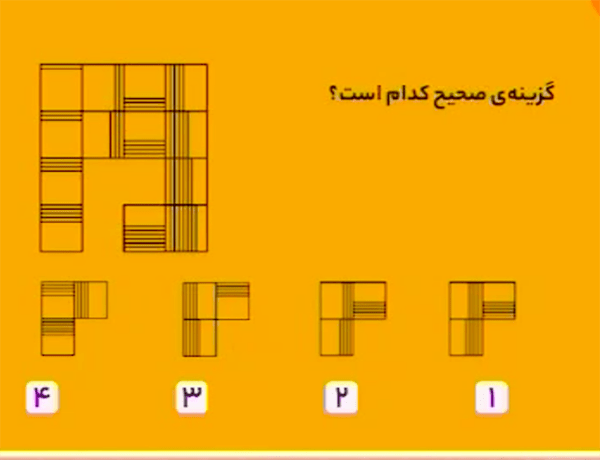
در هر ستون، از بالا به پایین، تعداد خط‌ها یکی‌یکی اضافه می‌شود.
در هر سطر، از چپ به راست، تعداد خط‌ها یکی‌یکی اضافه می‌شود ولی در هر سطر، خط‌های هر مربع، یکی‌درمیان، افقی و عمودی هستند.

پاسخ، گزینهٔ ۳ است.

از عدد سمت چپ شروع می‌کنیم. در این عدد، رقم اول را با رقم سوم و رقم دوم را با رقم چهارم جمع می‌کنیم. سپس این دو حاصلِ‌جمع را به یکدیگر می‌چسبانیم تا عدد میانی حاصل شود. بعد همین‌کار را روی عدد میانی انجام می‌دهیم تا عدد سمت راست به‌دست آید.
\[\begin{aligned}&8+7=15;\;2+8=10\quad 1510\\&1+1=2;\;5+0=5\quad 25\\&8278\;:\;1510\;:\;25\end{aligned}\]

در تبدیل $586321$ به $268$، رقم‌های زوج عدد اول را با ترتیب معکوس نوشته‌ایم و عدد دوم ساخته شده است. اگر رقم‌های زوج عدد $478321647$ را با ترتیب معکوس بنویسم عدد $46284$ ساخته می‌شود که در گزینهٔ ۱ آمده است.

گزینهٔ ۳ صحیح است.
برای اینکه مثلث بالا سمت چپ به مثلث بالا سمت راست تبدیل شود، گوشه‌های بالا و سمت راست این مثلث، به داخل تا شده است. شکل زیر را ببینید.

برای مثلث پایین هم باید همین کار را انجام داد.

پاسخ $32$ است.
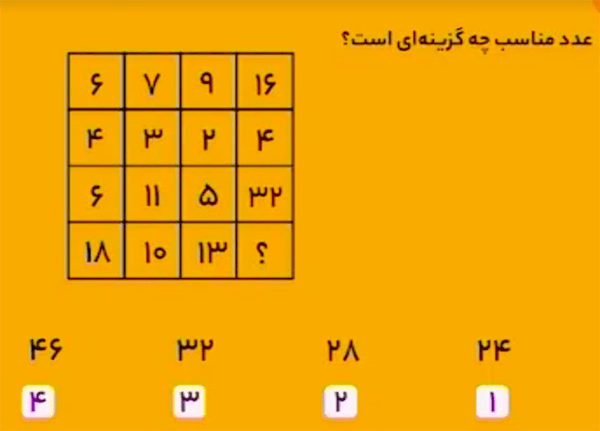
در هر ستون، ضرب اعداد سطر اول و دوم برابر جمع اعداد سطر سوم و چهارم است. بنابراین \[16\times 4=32+32\]