مسابقه تلویزیونی هوشیار – قسمت ۳۹

دنبالهٔ داده شده از دو دنباله تشکیل شده است:
\[{\color{red}1},{\color{blue}101},{\color{red}15},{\color{blue}4},{\color{red}29},{\color{blue}-93},{\color{red}43},{\color{blue}-190},{\color{red}?}\]
دنبالهٔ قرمزرنگ از عدد \(1\) شروع می‌شود و هر عدد بعدی آن، \(14\) واحد از عدد قبلی‌اش بیشتر است.
دنبالهٔ آبی‌رنگ از عدد \(101\) شروع می‌شود و هر عدد بعدی آن، \(97\) واحد از عدد قبلی‌اش کمتر است.
بنابراین، به‌جای علامت سؤال باید عدد \(57\) را قرار داد. زیرا:
\[43+14=57.\]

بازوی بالا در هر مرحله \(45\) درجه در جهت عقربه‌های ساعت حرکت می‌کند. و بازوی پایین در هر مرحله \(90\) درجه در جهت عقربه‌های ساعت می‌چرخد. بنابراین، به‌جای علامت سؤال باید شکل زیر را قرار داد.

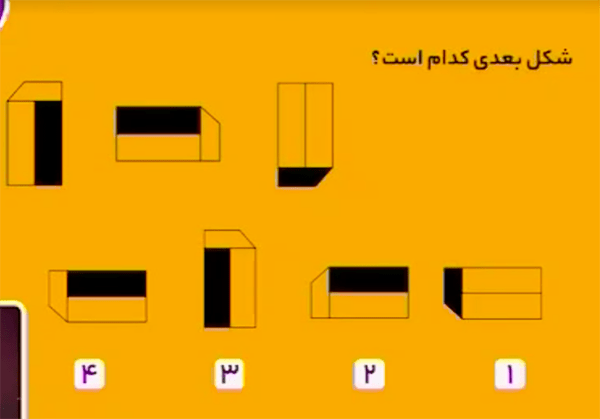
در هر مرحله شکل \(90\) درجه به صورت ساعتگرد می‌چرخد و هر بار یک قسمت متفاوت از مرحلۀ قبل آن سایه زده می‌شود. بنابراین، شکل زیر پاسخ درست است.

پاسخ $61$ است.
در \(473(50)\)، عدد \(50\) به‌صورت زیر، از \({\color{red}4}{\color{blue}7}{\color{green}3}\) به‌دست می‌آید.
\[{\color{red}4}0+{\color{blue}7}+{\color{green}3}=50.\]
در \(578(65)\)، عدد \(65\) به‌صورت زیر، از \({\color{red}5}{\color{blue}7}{\color{green}8}\) به‌دست می‌آید.
\[{\color{red}5}0+{\color{blue}7}+{\color{green}8}=65.\]
پس پاسخ از رابطهٔ زیر به‌دست می‌آید:
$$50+2+9=61$$

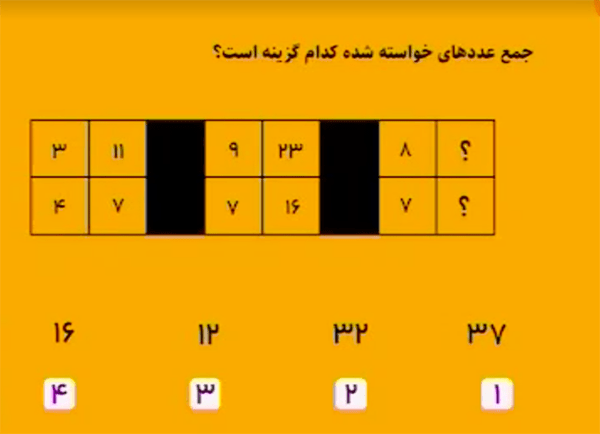
پاسخ $37$ است.
در هر مربع \(2\times2\)،
\(\bullet\) حاصل‌جمع اعداد ستون سمت چپ برابر است با عدد پایین ستون سمت راست.
\(\bullet\) و حاصل‌جمع اعداد سطر پایین برابر است با عدد بالای ستون سمت راست.
در جدول سمت چپ داریم:
\[\begin{aligned}&3+4=7\\&4+7=11.\end{aligned}\]
در جدول میانی داریم:
\[\begin{aligned}&9+7=16\\&7+16=23.\end{aligned}\]
در جدول سمت چپ داریم:
\[\begin{aligned}&8+7=15\\&7+15=22.\end{aligned}\]
پس پاسخ مسئله برابر است با:
\[15+22=37.\]
بنابراین، گزینهٔ ۱ درست است.

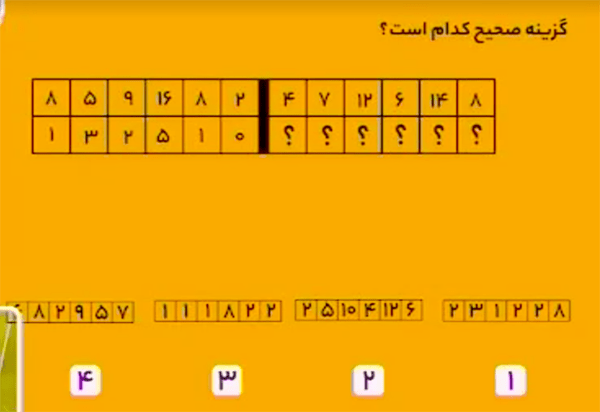
هر دو عدد پشت سرهم در قسمت پایین سمت چپ برابر است با مجموع دو عدد بالای آن. پس در مربع سمت راست هم داریم:
$$7+4=11$$ $$12+6=18$$ $$14+8=22$$
پس در قسمت پایین سمت راست باید داشته باشیم:
$111822$ و گزینهٔ ۳ صجیج است.

پاسخ $50$ است.
روابط زیر بین اعداد برقرار است:
$$11=10+1$$ $$14=11+3\times 1$$ $$23=14+3\times 3$$ پس باید داشته باشیم:
$$?=23+ 3\times 3\times 3$$ و $$131=?+3\times 3\times 3\times 3$$
روشن است که ۵۰ در دو تساوی بالا صدق می‌کند.

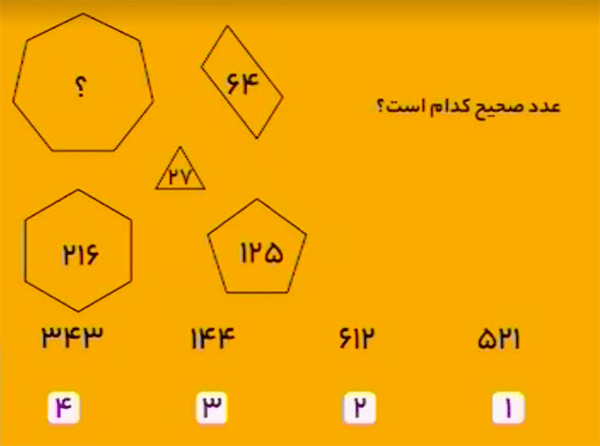
پاسخ $343$ است.
عدد درون هر یک از چند ضلعی‌ها برابر است با:

تعداد اضلاع $\times $ تعداد اضلاع $\times$ تعداد اضلاع

پس جواب برابر است با $$7\times 7\times 7=343$$

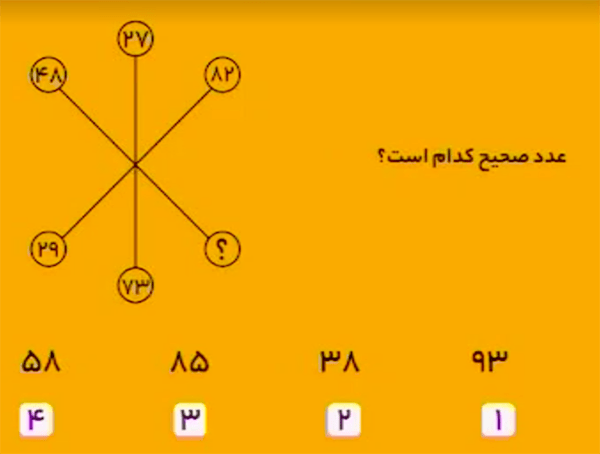
پاسخ $85$ است. اعداد درون دایره‌های پایین با این قانون از دایره‌های روبه‌روی آن‌ها ساخته می‌شود: دهگان عدد جدید یکان عدد روبه‌رو است و یکان عدد جدید یک واحد بیشتر از دهگان عدد روبه‌رو است.