مسابقه تلویزیونی هوشیار – قسمت ۴۱

گزینهٔ ۴ صحیح است.
در هر سطر یا هر ستون، دایره‌های سیاه کل جایگاه‌ها را پر می‌کنند. بنابراین در سطر سوم دو جایگاه فعلا سیاه شده است پس باید سه جایگاه دیگر هم سیاه شود.

پاسخ $47632$ است.
دو رقم سمت راستِ هریک از اعداد دیگر را به‌عنوان یک عدد دورقمی در نظر بگیرید و آن را در خودش ضرب کنید؛ حاصل یک عدد سه رقمی است که همان سه رقم سمت چپ است.
\[\begin{aligned}84129&\\&29\times 29=841\\32418&\\&18\times 18=324\\36119&\\&19\times 19=361\\67626&\\&26\times 26=676\\72927&\\&27\times 27=729\end{aligned}\]
اما 47632 چنین خاصیتی ندارد. چون
\[32\times 32=1024\neq 476\]

پاسخ $1097$ است. رابطهٔ زیر بین اعداد وجود دارد:
\[\begin{aligned}5&=4+1\\8&=5+3\\17&=8+3\times 3\\44&=17+3\times 3\times 3\\125&=44+3\times 3\times 3\times 3\\368&=125+3\times 3\times 3\times 3\times 3\end{aligned}\]پس باید داشته باشیم
$$?=368+3\times 3\times 3\times 3\times 3\times 3=1097$$

راه حل دیگر: روابط زیر هم بین اعداد برقرار است:
\[\begin{aligned}5&=4\times 3-7\\8&=5\times 3-7\\17&=8\times 3-7\\44&=17\times 3-7\\125&=44\times 3-7\\368&=125\times 3-7\\1097&=368\times 3-7\end{aligned}\]

پاسخ $32$ است.
در شکل سمت چپ و میانی، عدد داخل مثلث برابر است با حاصل‌ضرب دو ضلع کناری به اضافهٔ ضلع پایین به اضافهٔ ۲.
\[\begin{aligned}36&=4\times 8+2+2\\30&=6\times 4+4+2\\32&=3\times 8+6+2\end{aligned}\]

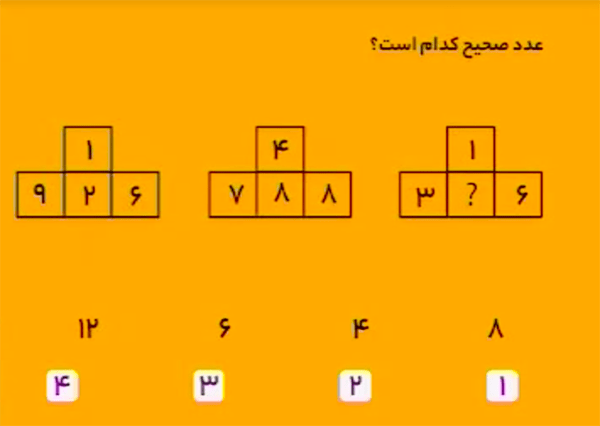
پاسخ $8$ است.
روابط زیر برقرار است:
\[\begin{aligned}16&=9\times 2-2\\48&=7\times 8-8\\16&=3\times 8-8\end{aligned}\]

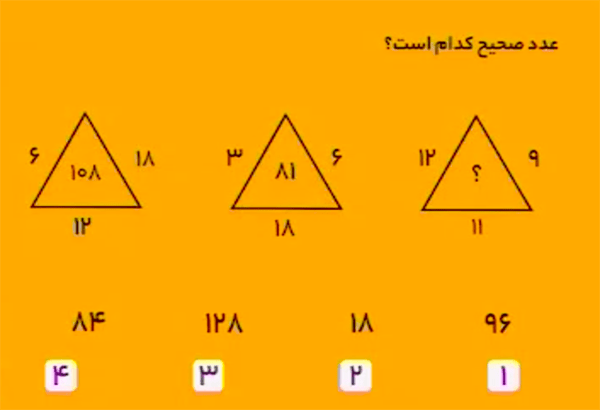
پاسخ $96$ است.
در هر شکل، عدد داخل مثلث برابر است با سه برابر مجموع اعداد روی سه ضلع.
\[\begin{aligned}108&=3\times (6+12+18)\\81&=3\times (3+18+6)\\96&=3\times (12+11+9)\end{aligned}\]

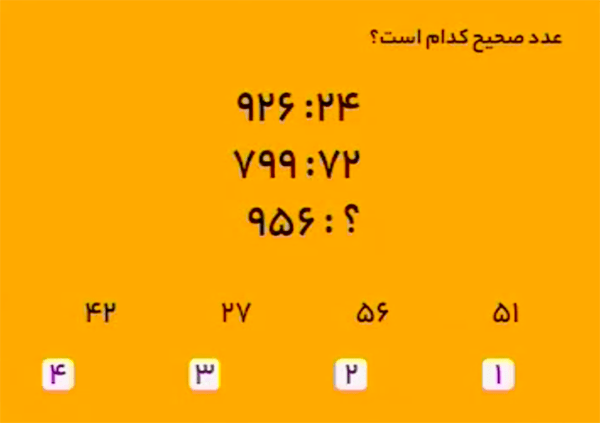
پاسخ $51$ است.
در هر سطر، عدد سمت راست برابر است با حاصل‌ضرب صدگان در دهگان به اضافهٔ یکان عدد سمت چپ.
\[\begin{aligned}24&=9\times 2+6\\72&=7\times 9+9\\51&=9\times 5+6\end{aligned}\]

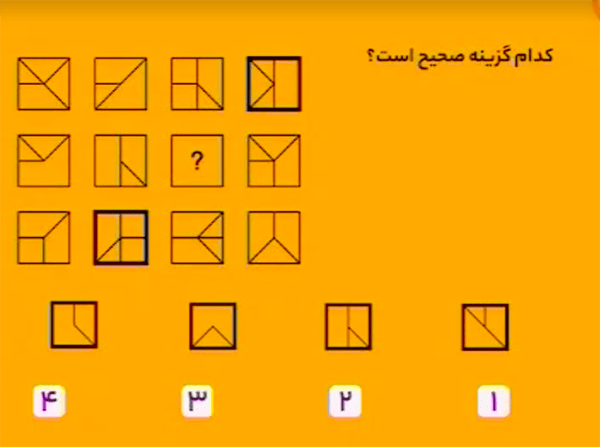
گزینهٔ ۴ صحیح است.
در هر سطر مربع سوم از چپ از ترکیب دو مربع قبلی ساخته می‌شود با این شرط که در هر جایگاه اگر دو شکل یکسان در مربع اول و دوم باشد، در مربع سوم شکل دیگر در آن جایگاه ظاهر می‌شود.
قانون بالا در ستون‌ها هم برقرار است.

پاسخ گزینهٔ ۴ است.
در هر سطر مربع‌هایی که دور آن‌ها سیاه شده است، از ترکیب مربع‌های دیگر همان سطر ساخته می‌شود با این قانون که خطوطی که فقط یکبار ظاهر شده‌اند در مربع دور سیاه هم وجود دارند.

پاسخ $9$ است. از راست به چپ مجموع اعداد هر ستون برابر است با \(5\)، \(6\)، \(7\)، و \(8\). پس ستون آخر باید عدد $9$ باشد.