مسابقه تلویزیونی هوشیار – قسمت ۴۳

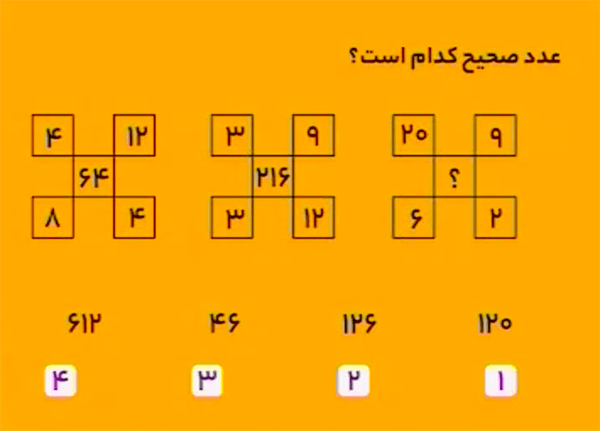
اعداد میانی از حاصل‌ضرب عدد سمت چپ-بالا در عدد سمت راست-پایین در اختلاف بین عدد سمت راست-بالا و سمت چپ-پایین به دست می‌آید.
در شکل سمت چپ:
$$64=(12-8)\times 4\times 4$$
در شکل میانی:
$$216=(9-3)\times 12\times 3$$
پس در شکل سمت راست:
$$(9-6)\times 20\times 2=120$$
بنابراین، گزینهٔ ۱ درست است.

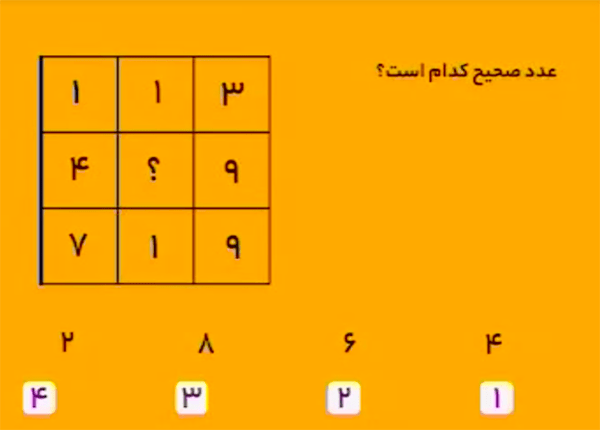
اصل سؤال به شکل زیر است:
به‌جای علامت سؤال چه عددی باید قرار داد؟

پاسخ، عدد 4 است.
در هر سطر، اگر حاصل‌ِجمع عدد سمت‌چپ و عدد میانی را با یک جمع بزنیم عدد سمت راست به‌دست می‌آید. برای مثال، در سطر اول داریم:
\[(2+3)+1=6\]

پاسخ $160$ است.
این دنباله با عدد \(784\) شروع می‌‌شود و اعداد بعدی از حاصل‌ضرب رقم صدگان در عدد دورقمی سمت راست آن به‌دست می‌آید:
\[\begin{aligned}&7\times84=588\\&5\times88=440\\&4\times40=160\\&1\times60=60.\end{aligned}\]

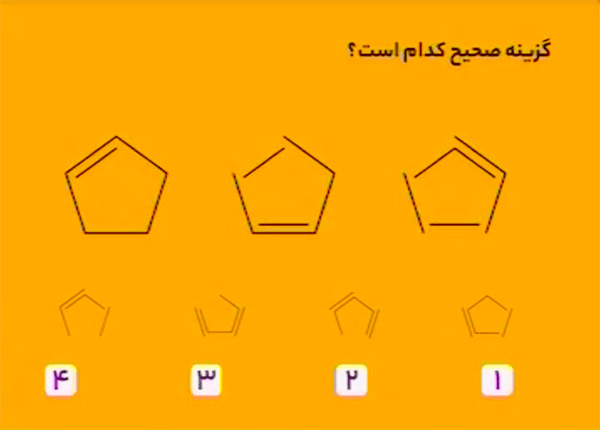
شکل سمت چپ با قانون‌های زیر به شکل میانی تبدیل می‌شود.
\(\bullet\) ضلعی از پنج ضلعی که خط زیر آن است، حذف می‌شود.
\(\bullet\) ضلع (ضلع‌های) حذف شده پادساعت‌گرد می‌چرخد و روی دو ضلع جلوتر قرار می‌گیرد.

شکل دوم نیز با همین قانون‌ها به شکل سوم تبدیل می‌شود.
برای پیدا کردن گزینهٔ درست باید شکل سوم را با قانون گفته شده تبدیل کنیم.
بنابراین، گزینهٔ ۱ درست است.

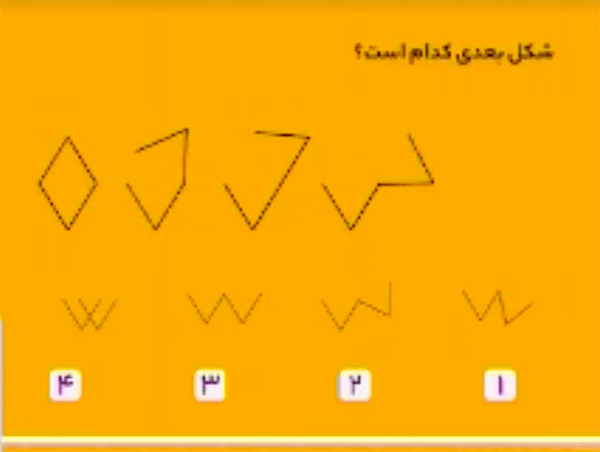
پاسخ گزینهٔ ۲ است.
دو ضلع بالایی لوزی در هر مرحله $45$ درجه حول رأس سمت راست لوزی دوران می‌کند.

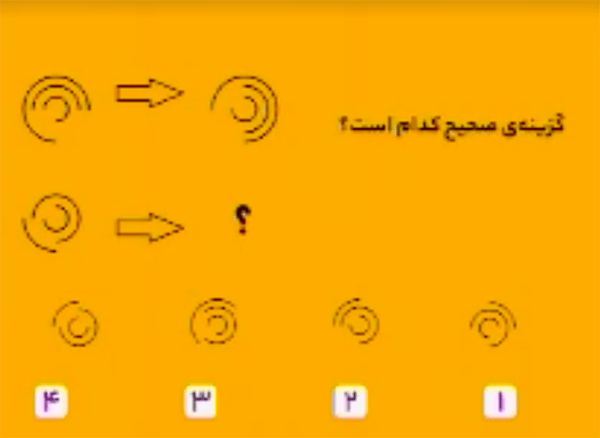
پاسخ گزینهٔ ۴ است. هر یک از منحنی‌ها $90$ درجه خلاف جهت عقربه‌های ساعت دوران کرده است.

عدد دوم از جابه‌جا کردن رقم‌های عدد اول ساخته شده است.
عدد سوم برابر است با مجموع عدد اول و دوم.
عدد چهارم از جابه‌جا کردن رقم‌های عدد سوم ساخته شده است.
عدد پنجم برابر است با مجموع عدد سوم و چهارم. $$77+77=154$$ با ادامهٔ قانون‌های بالا اعداد دیگر دنباله ساخته می‌شود.

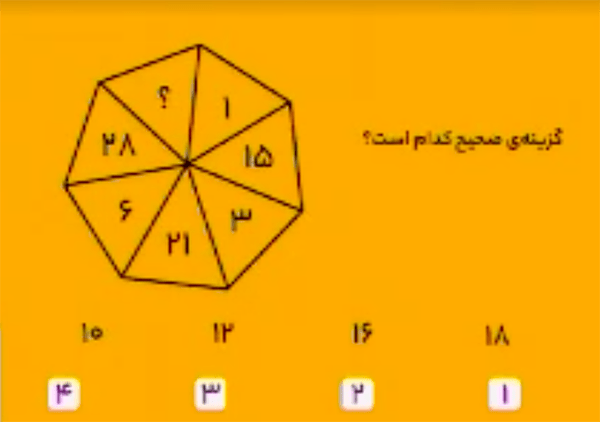
پاسخ $10$ است. از $1$ شروع می‌کنیم و در هر مرحله دو جایگاه در جهت عقربه‌های ساعت به جلو می‌رویم تا دنبالهٔ زیر تشکیل شود. $$1,3,6,?, 15,21,28$$
$$3=1+2$$ $$6=3+3$$ $$10=6+4$$ $$15=10+5$$ $$21=15+6$$ $$28=21+7$$

پاسخ $9$ است.
نسبت مهمان‌هایی که چای تلخ نخواستند به کل مهمان‌ها به روش زیر محاسبه می‌شود:$$\frac{1}{4}+\frac{5}{8}+\frac{1}{16}=\frac{4+10+1}{16}=\frac{15}{16}$$ پس $\frac{1}{16}$ مهمان‌ها چای تلخ خواستند. $$\frac{1}{16}\times 144=9$$