مسابقه تلویزیونی هوشیار – قسمت ۴۵

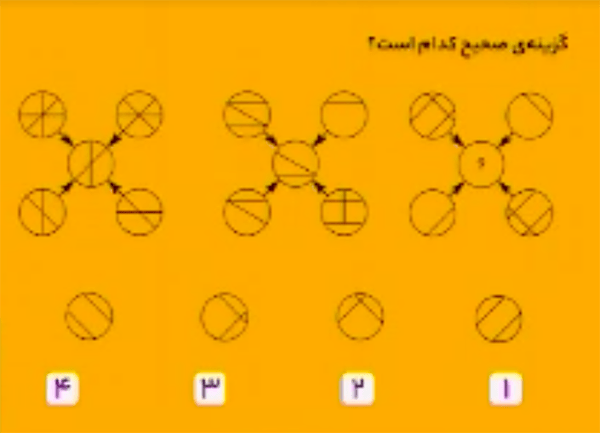
پاسخ گزینهٔ ۳ است.
در هر دو قسمت روبه‌رو، مانند شکل زیر، در مجموع شش‌تا دایرهٔ توخالی و سه‌تا دایرهٔ خط‌دار دیده می‌شود.

بنابراین، در قسمت حذف شده باید دو دایرهٔ توخالی و یک دایرهٔ خط‌دار داشته باشیم.

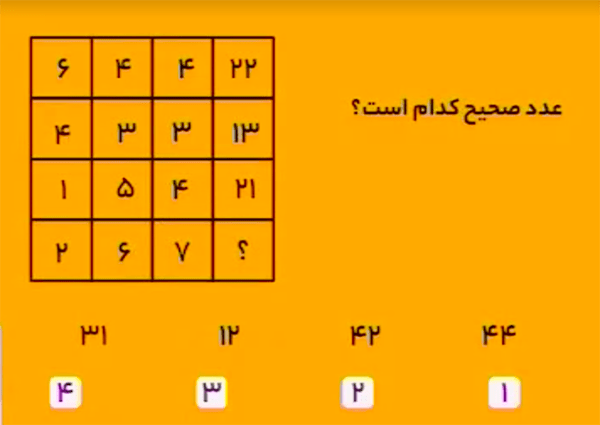
پاسخ دستهٔ ۲ است.
ویژگی مشترک بین اعداد دستهٔ ۱ این است که باقی‌ماندهٔ تقسیم هریک از آن‌ها بر $4$ برابر $3$ است.
ویژگی مشترک بین اعداد دستهٔ ۲ این است که باقی‌ماندهٔ تقسیم هریک از آن‌ها بر $4$ برابر $2$ است.
ویژگی مشترک بین اعداد دستهٔ ۳ این است که باقی‌ماندهٔ تقسیم هریک از آن‌ها بر $4$ برابر $1$ است.
ویژگی مشترک بین اعداد دستهٔ ۴ این است که باقی‌ماندهٔ تقسیم هریک از آن‌ها بر $4$ برابر $0$ است.
چون باقی‌ماندهٔ تقسیم $6$ بر $4$ برابر $2$ است پس $6$ عضو دستهٔ دوم است.

پاسخ $44$ است.
در هر سطر حاصل‌ضرب ستون دوم و سوم به اضافهٔ ستون اول با ستون چهارم برابر است.$$22=6+(4\times 4)$$ $$13=4+(3\times 3)$$ $$21=1+(5\times 4)$$ با توجه به الگوی بالا، برای سطر پایین داریم:
$$2+(6\times 7)=2+42=44$$ پس به‌جای علامت سؤال باید عدد \(44\) را قرار دهیم.
بنابراین، گزینهٔ ۱ درست است.

پاسخ $7$ است.
در سطر بالا، هریک از رقم‌های \(1\) تا \(9\) دقیقاً یک‌بار دیده می‌شود. در سطر میانی هم، هریک از رقم‌های \(1\) تا \(9\) دقیقاً یک‌بار دیده می‌شود. اگر به‌جای علامت سؤال عدد \(7\) را قرار دهیم، آن‌وقت در سطر پایین هم هریک از ارقام \(1\) تا \(9\) دقیقاً یک‌بار دیده می‌شوند.

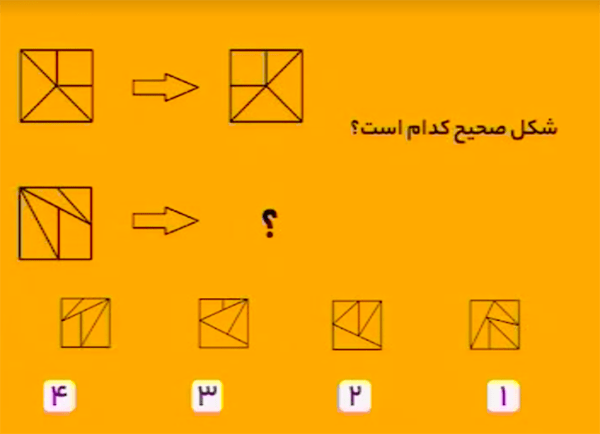
پاسخ گزینهٔ ۴ است.
در نمونهٔ داده شده، شکل به تصویر آینه‌ای‌اش تبدیل شده است. پس باید دنبال تصویر آینه‌ای شکل داده شده بگردیم که همان گزینهٔ ۴ است.

پاسخ $29$ است.
دنبالهٔ داده شده از دو دنبالهٔ متفاوت زیر تشکیل شده است:$$1,4,7,10$$ و $$1,8,15,22,?$$ می‌بینیم که هر جملهٔ این دنباله $7$ واحد از قبلی بیشتر است. پس جملهٔ بعدی آن برابر است با: $$22+7=29$$

پاسخ $405$ است.
نسبت هر دو جملهٔ پشت‌سر هم این دنباله به شکل زیر است:$$2,1.5,2,1.5,2,…$$ پس جملهٔ بعدی آن به شکل زیر به‌دست می‌آید:$$270\times 1.5=405$$

پاسخ $113$ است.
اگر هر یک از اعداد چهار رقمی را به عنوان دو عدد دو رقمی در نظر بگیریم، عدد داخل پرانتز با مجموع آن دو عدد دو رقمی برابر است.
$$38+74=112$$ $$28+69=97$$ $$86+27=113$$

گزینهٔ ۲ صحیح است.
فقط خطوطی که دقیقاً دوبار در چهار دایره اطراف در یک موقعیت ظاهر می شوند به دایره مرکزی منتقل می شوند.