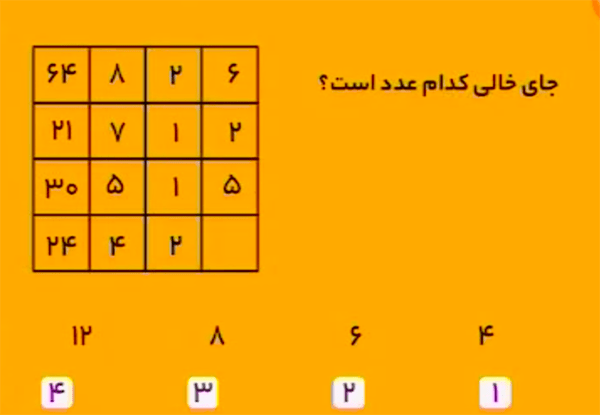
پاسخ $4$ است.
در هر سطر، حاصلضرب «ستون دوم» در «مجموع ستون سوم و چهارم» با ستون اول برابر است. روابط زیر را ببینید:$$64=8\times (2+6)$$ $$21=7\times (1+2)$$ $$30=5\times (1+5)$$ پس برای سطر چهارم هم باید داشته باشیم: $$24=4\times (2+?)$$
در نتیجه، \(2+?\) باید برابر \(\frac{24}{4}\)، یا \(6\) باشد. بنابراین، بهجای علامت سؤال باید عدد \(4\) را قرار داد.
دو عدد $70$ و $76$ باید جابهجا شوند.
با جابهجایی این دو عدد، دنبالههای زیر را خواهیم داشت:
\[\begin{aligned}&88,84,76,60\\&97,91,82,70.\end{aligned}\] حال، اختلاف هر دو عضو متوالی دنبالهٔ اول، دنبالهٔ
\[4,8,16\] را میسازد؛ و اختلاف هر دو عضو متوالی دنبالهٔ دوم، دنبالهٔ
\[6,12,18\] را تشکیل میدهد.
پاسخ $74$ است.
دنبالهٔ داده شده با عدد \(24\) شروع میشود و هریک از اعداد بعدی از حاصلجمع عدد قبلی با حاصلضرب رقمهایش بهدست میآید:
\[\begin{aligned}&24+(2\times4)=32\\&32+(3\times2)=38\\&38+(3\times8)=62\\&62+(6\times2)=74.\end{aligned}\]
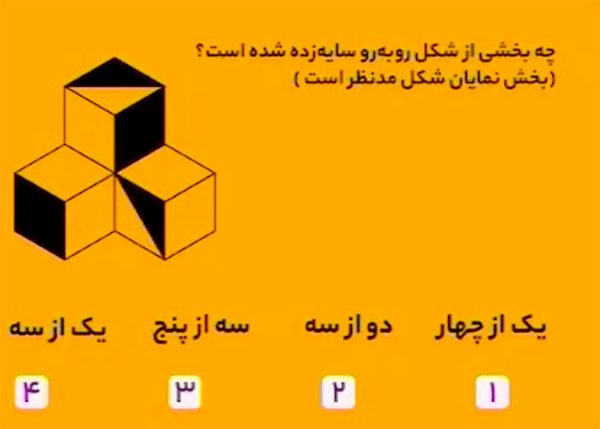
پاسخ یک از سه است.
اگر مطابق شکل زیر دو قسمت رنگ شده را به بالا انتقال دهیم، متوجه میشویم که یکی از سه مکعب شکل کامل رنگ شده است.

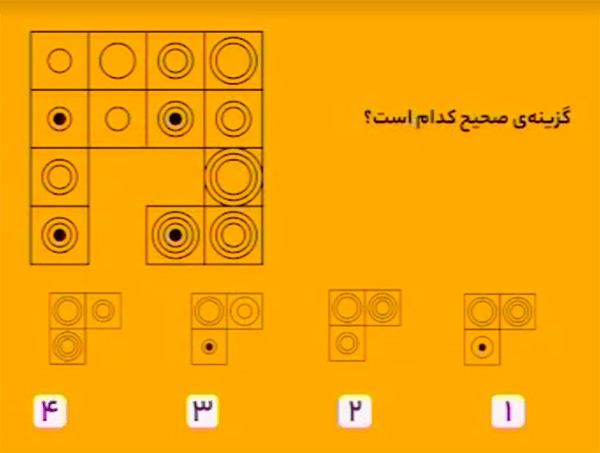
پاسخ گزینهٔ ۲ است.
شکلهای سطر اول و دوم به ترتیب به سطر سوم و چهارم منتقل شدهاند با این تفاوت که دور هر یک از آنها یک دایره رسم شده است. همچنین، میتوان گفت شکلهای ستون اول و دوم به ترتیب به ستون سوم و چهارم منتقل شدهاند با این تفاوت که دور هر یک از آنها یک دایره رسم شده است.
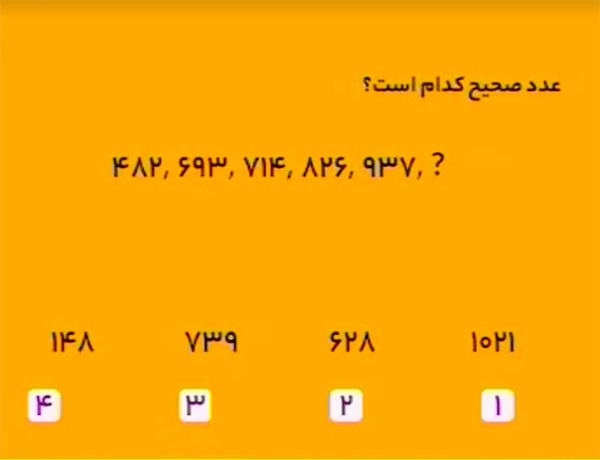
پاسخ $148$ است.
در دنبالهٔ داده شده، ارقام
\[4,8,2,6,9,3,7\] با ترتیب یکسان در قالب اعداد سهرقمی تکرار شدهاند. یعنی اگر ویرگولها را ننویسیم، داریم:
\[{\color{gray}48269371}{\color{black}48269371}\] یا در تصویر داده شده:

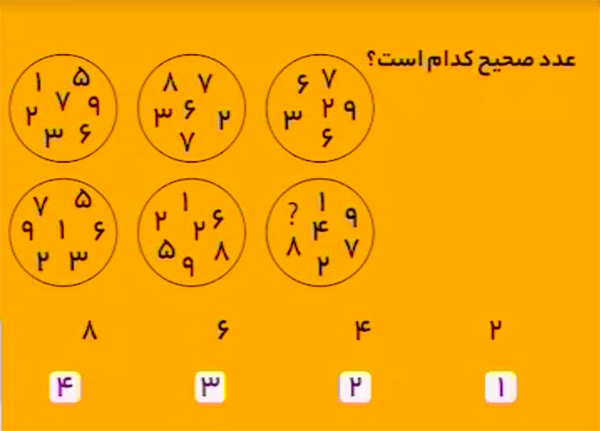
پاسخ $2$ است.
مجموع اعداد داخل هر یک از دایرهها برابر $33$ است. مجموع اعداد موجود در دایرهٔ آخر $31$ است پس باید عدد $2$ جایگزین علامت سؤال شود.
پاسخ دستهٔ ۳ است.
ویژگی مشترک اعداد دستهٔ ۱ این است که باقیماندهٔ تقسیم آنها بر $7$ برابر $0$ است.
ویژگی مشترک اعداد دستهٔ ۲ این است که باقیماندهٔ تقسیم آنها بر $7$ برابر $2$ است.
ویژگی مشترک اعداد دستهٔ ۳ این است که باقیماندهٔ تقسیم آنها بر $7$ برابر $1$ است.
ویژگی مشترک اعداد دستهٔ ۴ این است که باقیماندهٔ تقسیم آنها بر $7$ برابر $6$ است.
چون باقیماندهٔ تقسیم $99$ بر $7$ برابر $1$ است پس $99$ عضو دستهٔ ۳ است.
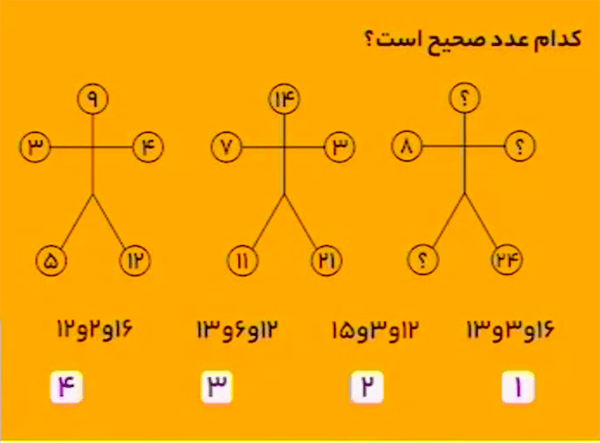
پاسخ گزینهٔ ۱ است.
مطابق شکل زیر دایرهها را نام گذاری میکنیم.

در هر دایره روابط زیر برقرار است:
\[\begin{aligned}a+c&=d\\b+e&=a\\b\times c&=d.\end{aligned}\]
پس در شکل سوم خواهیم داشت:
\[\begin{aligned}a+8=24 &\Rightarrow a=16\\b\times 8=24 &\Rightarrow b=3\\e+3=16 &\Rightarrow e=13.\end{aligned}\]












ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️